알고리즘
1.(군에서) 알고리즘 공부를 해보니
(군에서) 알고리즘 공부를 해보니 계기 > 최근 알고리즘 문제해결 전략(종만북)을 공부하고 있다. 지금까지는 그냥 만나는 문제만 풀었고 분류와 체계를 가지고 공부할 생각은 못해봤다. 그렇게 간절한 건 아니었을지도 모른다. 뭘 공부해야 하는지도 모르고 그냥 공부하고
2.알고리즘 문제 리스트(기초1~중급3)
(최백준님 강의에 있는 문제들을 리스트화 했다.)내가 푸려고 만든 리스트이지만 시작하는 누군가에게 도움이 될까 싶어 올려본다.
3.BOJ 17298 오큰수
BOJ 17298 오큰수처음 딱 본 순간 생각보다 간단한데? 하면서 그냥 아래와 같이 naive 하게 풀었다.이때는 빨리 풀고 다음문제 해야지라는 생각에 입력 크기를 못본듯. 이렇게 풀고 나니 시간초과가 떴다.그제서야 입력 크기를 보니 너무 당연했다.(1e6)^2 이
4.BOJ 1912 연속합
요즘 너무 이론적인 것과 형식에 치우쳤는지 DP 하면 그냥 일단 필요한 것들을 쳐놓고 시작했다.문제집을 만들어놓고 푼 것과 LIS에 너무 집착한 것도 한 몫을 한것같다.이런 행동이 시야를 좁혔고, 엄청 간단한 문제임에도 구현을 바로 하지 못하고 헤매었다.직관적으로 코드
5.C++ map
mapmultimapunordered_mapkey value, mapped value로 이루어진 자료구조다.key 중복이 불가능하다. (unique)내부 비교 객체(기본은 less)에 의해서 정렬되어 삽입된다. (따라서 항상 정렬되어 있음)iterator를 사용해 순차
6.BOJ 7569 토마토
가능한 깊이(depth) 까지 최대한 내려간 것을 골라야함. (지난 일 수)사과가 모두 익는 경우는 BFS 탐색을 마칠 때임.(큐 안에는 안익은 사과만 들어간다)문제에서 최소 일 수를 구하라고 한다.BFS를 사용할 때 방문한 곳은 다시 방문하지 않으므로 이미 경로가 최
7.0-1 BFS

최근 기존과는 다른 유형의 BFS 문제를 몇 개 만났다.처음엔 별 생각 없이 예외처리로 풀었다.그러다 방금 이 문제를 푸는데 불현듯cost가 적은 것을 먼저 처리해야 하니 queue 앞에 삽입하면 좋겠다. 그러려면 deque를 사용해야겠는데.. 맞나?이런 생각을 했다.
8.BOJ 13023 ABCDE
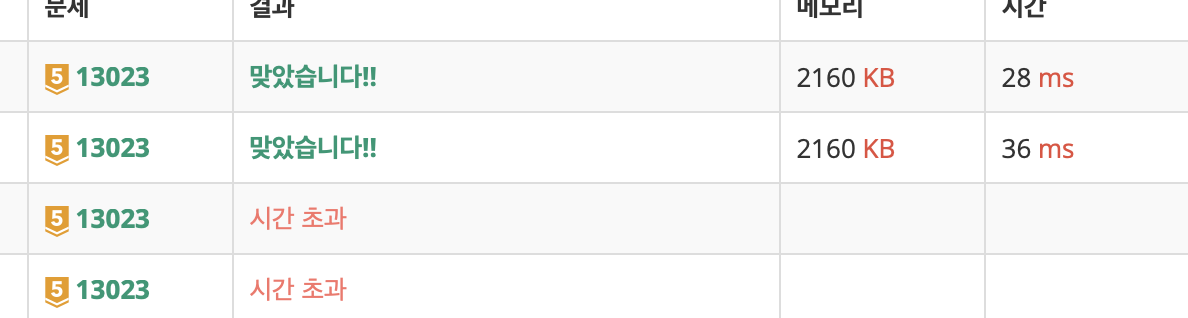
맞는 솔루션인것 같은데, 시간초과가 발생했다.사이즈 계산해보니 탐색 중 시간초과가 나겠다고 예상했다.원인은 원소 접근이었다. O(1)에 원소를 접근할 방법을 고민해보게 되었다.(코드의 많은 부분이 생략되었다)아이디어는 무방향 간선에서 두개의 Edge에서 접근할 원소들을
9.BOJ 1707 이분 그래프
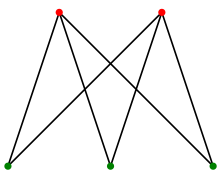
문제그래프 이론에서, 이분 그래프(二分graph, 영어: bipartite graph)란 모든 꼭짓점을 빨강과 파랑으로 색칠하되, 모든 변이 빨강과 파랑 꼭짓점을 포함하도록 색칠할 수 있는 그래프이다.문제를 푸려다가 문제에 나와있는 말만으로는 이해가 잘 안되어 찾아봤다
10.BOJ 13023 ABCDE 재시도
다시 시도했는데 틀렸다.여러 원소를 다양한 각도에서 접근하면서 사이클도 막아야하는데, 방문 배열 전체를 초기화하는 방법밖에 생각이 나지 않았다.그래서 그냥 돌린 첫번째 결과 실패. 시간 초과는 아니었지만 당연히 커버되지 않는 케이스가 있다.두 번째 시도에서 재귀를 빠져
11.BOJ 9251 LCS, 9252 LCS2
두 문자열의 공통 부분중 가장 긴 것의 길이를 찾는 문제이다.길이만 찾으면 되므로 다른 문제와 다를 바가 없었다.A의 인덱스와 B의 인덱스를 증가시키며 둘이 일치하면 길이 + 1한다.수식 문자 일치할 경우dpi = dpi+1+1일치하지 않을 경우dpi = max(dpi
12.BOJ 1655 가운데를 말해요
보자마자 에디터 문제의 아이디어가 떠올랐다.얘는 우선순위 큐로 커서를 유지하면 되겠구나.왼쪽은 max heap, 우측은 min heap으로 만들어가운데 값을 항상 쓸 수 있게 유지하려는 전략을 세웠다.짝수 원소 개수의 경우에는 left.size() == right.si
13.BOJ 1914 하노이 탑
문제 설명 큰 문제를 작은 문제로 쪼개는 아이디어. 알고나니 분할정복으로써 당연한 아이디어고 절차였다. 쪼개는 프로세스를 생각하는 게 중요해 보인다. >한 문제는 3과정으로 쪼개진다. 제일 큰 판을 제외한 나머지를 via로 이동 제일 큰 판을 to로 이동 나머지를 t
14.BOJ 11051, 11401 이항 계수
이항 계수 2이항 계수 3문제는 2나 3이나 비슷하다.그러나 크기가 많이 다르다.2는 간단한 DP로 해결가능하다.3은 nCk를 적당한 소수로 모듈로 연산한 결과를 출력하는 문제다.이 문제도 처음에 DP로 접근하였으나 몇가지 다른 스킬들이 필요하다.세 수식을 각각 a,
15.BOJ 1629 곱셈
컴퓨터의 정수형이 소수점 아래를 표현하지 못하는 점을 고려할 때,어떤 수의 거듭제곱은 다음과 같이 나타낼 수 있다.상단 식은 n이 짝수인 경우, 하단 식은 홀수인 경우이다.이 점을 이용해 분할정복 알고리즘을 사용하면, 매번 문제의 크기가 1/2로 줄어드는 솔루션을 작성
16.BOJ 2629 양팔저울
아주 간단한 DP인데, 배워야 할 점이 있다.나는 음수가 나오는 경우를 없애기 위해 한쪽으로 몰아넣고 +, -로 해결하려고 했다.그래도 음수가 나오는 경우가 생길 수 있었다. 테스트케이스는 음수를 고려하고 들어오는게 아니기 때문에.이 점을 5달 전에 알게되었지만, 코드