공식
점이 (x1, y1, z1), (x2, y2, z2)가 있다고 가정해보자.
증명
일단 원점 O와 3차원 좌표 v1을 두고 설명하겠습니다.
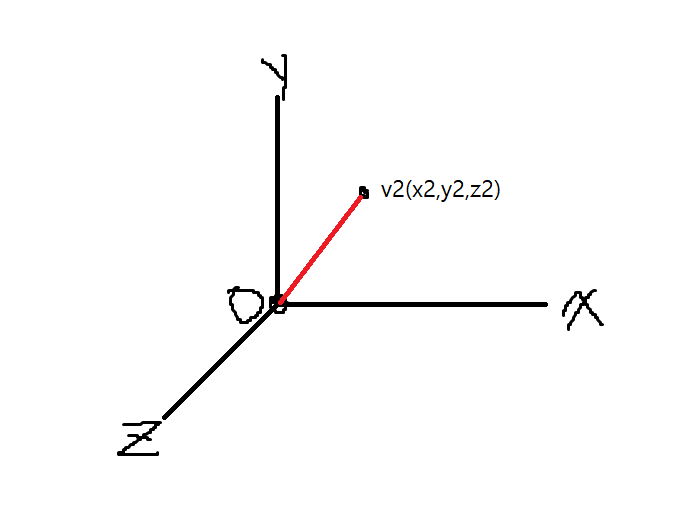
x, z축 상에 좌표를 잡고 직각삼각형을 만들어보겠습니다.

그러고 각각 x축, z축에 직각으로 선을 그어보겠습니다.
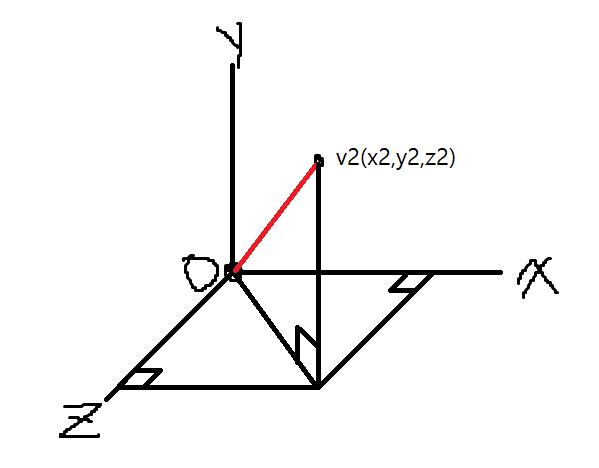
각각의 접점은 피타고라스의 정리를 통해 구할 수 있습니다.

그럼 우리가 최종적으로 구하려는 원점과 v2와의 거리도 구할 수 있습니다.
여기에 원점 대신 원하는 좌표를 넣으면 해당 점과 점 사이의 거리를 구할 수 있게 됩니다.
원점과 점에 대한 공식으로 점과 점사이 거리 구하기
수학의 영역에서는 빛이 포함되어있지 않아
어느 관점에서 점과 점사이 거리를 바라보던 그 거리는 변화하지 않습니다.
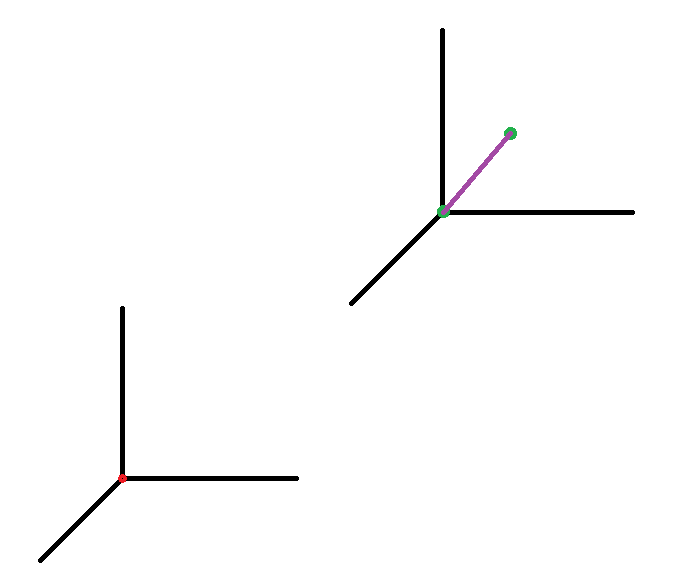
위의 사진처럼 초록색 점과 점 사이의 거리를 빨간색 점 좌표에서 바라보고 있다고 해보자.
빨간색 점에서 보면 저기 좌표의 중앙에 있던 초록색 점은 더이상 원점이 아니게 됩니다.
그러면 원점과 점 사이 거리 공식을 사용할 수 없게 됩니다.
그런데 위에서 말했듯이 어떤 관점에서 바라보던 그 거리는 변화하지 않습니다.
즉, 빨간색 점에서 봐도 저 보라색 거리는 변화하지 않습니다.
그러면 두 초록색 점을 빨간색 점으로 가지고 와도 거리는 변화하지 않습니다.

위 사진과 같이 빨간 점의 관점에서 바라보므로 빨간 점이 원점이 됩니다.
그러면 원래 원점이였던 초록색 점은 일정한 값을 가지게 됩니다.
그리고 이동 역변환을 통해 초록색 좌표를 빨간색 좌표로 가지고 오면 길이는 변화하지 않으면서
원점과 점 사이 거리 공식으로 점과 점사이 거리를 구할 수 있습니다.
좌표를 이동시킬 때도 빛이 없어 시간과 속력이 정의되지 않아 시공간 운동 변환이 아니라 단순히 공간 자체만 딱 이동시키는 것입니다.
절대값 도입
현재 증명 방식은 만약 좌표가 음수에 있을 경우 길이가 음수가 나와버려 길이는 양수여야 한다는 것에 위배되므로 절대값을 도입해 더 안전하게 증명할 수 있습니다.
그러면 각각의 길이를 아래처럼 나타낼 수 있습니다.
그러고 원점과 점 사이 거리를 이전과 같이 증명하게 되면 결과는 똑같이 나옵니다.
그러나 그 증명 과정에서 길이가 음수가 되는 위험성을 없애 더욱 안전해졌습니다.
공식 활용
해당 공식은 게임 내에서 두 오브젝트 사이의 거리를 확인하거나, 두 원의 충돌체크를 하는 등 다양한 방면으로 활용될 수 있습니다.