An Introduction to Graph Neural Network (GNN) for Analyzing Structured Data

Author: Shanon Hong
번역 및 각색: 사용자

이 글은 Shanon Hong의 “An Introduction to Graph Neural Network(GNN) for Analyzing Structured Data”를 저자 허락 하에 번역하고 각색한 내용. GNN은 그래프 데이터를 분석하는 데 매우 효과적인 방법으로, 이 글에서는 GNN에 대한 기초 이론부터 실제 응용 사례까지 폭넓게 설명.

🏖️ 1. Graph Neural Network(GNN)란?

1.1 GNN의 정의

GNN(Graph Neural Network)은 그래프 데이터를 직접 분석할 수 있는 신경망 모델입니다.
그래프는 점(노드)과 선(엣지)으로 구성된 데이터 구조로, 점 간의 관계나 상호작용을 나타냅니다.
GNN의 목적: GNN은 점, 선, 그래프 전체에서 예측을 수행할 수 있습니다. 특히 GNN은 그래프에서 점의 상태를 이웃 점들과의 연결을 통해 업데이트하는 방식으로 학습을 진행합니다.

1.2 GNN의 핵심 개념

Node embedding: 그래프에서 각 점의 상태는 이웃한 점들과의 관계를 통해 업데이트됩니다. 이 최종 상태는 node embedding이라고 하며, 이 embedding을 통해 예측 작업이 이루어집니다.
GNN은 주로 그래프의 연결 구조와 노드의 특징(feature)을 이용해 학습을 진행합니다.

🏖️ 2. 그래프란 무엇인가?

2.1 그래프의 정의

그래프는 점(노드, V)과 그 점을 연결하는 선(엣지, E)으로 구성된 데이터 구조입니다.
대표적인 그래프의 예시:
- 소셜 네트워크에서의 친구 관계
- 유저와 유튜브/넷플릭스 영상 간의 감상 여부를 나타내는 관계

2.2 그래프의 수학적 정의

그래프는 수학적으로 $G = (V, E)$ 로 표현되며, 여기서 V는 점의 집합, E는 선의 집합을 나타냅니다.
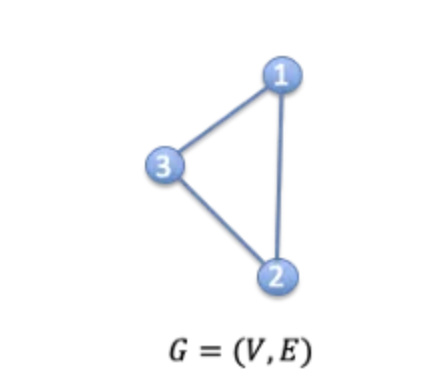
예를 들어, 아래 그래프는 $G=($ {1, 2, 3} $, {$ {1, 2} $, ${2, 3}$
, {1, 3} $}$ )$으로 정의될 수 있습니다.

2.3 그래프의 표현 방법

그래프는 인접행렬(Adjacency Matrix)로 표현될 수 있습니다. n개의 점이 있을 때 인접행렬의 크기는 n × n입니다.
또한, 점의 특징을 표현한 Feature Matrix도 있습니다. 점의 개수가 n, 특징의 개수가 f일 때, feature matrix의 크기는 n × f입니다.

🏖️ 3. 그래프 데이터를 분석하기 어려운 이유

3.1 유클리드 공간이 아님

그래프 데이터는 유클리드 공간(2차원/3차원 공간)에 쉽게 매핑되지 않습니다.
이미지, 음성, 시계열 데이터는 2차원 혹은 3차원 공간에서 표현 가능하지만, 그래프는 점과 선의 관계로 인해 복잡하고 해석이 어렵습니다.

3.2 고정된 형태가 아님

동일한 인접행렬을 가지더라도 그래프의 형태가 다를 수 있습니다. 이로 인해 시각적으로 다르게 보이는 그래프를 동일하게 분석할지 다르게 분석할지 결정하는 것이 어렵습니다.

3.3 시각화의 어려움

점의 수가 수백, 수천 개에 이르는 대규모 그래프는 시각적으로 해석하기 어렵습니다. 그래프의 복잡성 때문에 그래프 시각화를 위한 연구도 활발히 진행되고 있습니다.

🏖️ 그래프를 사용하는 이유

관계, 상호작용과 같은 추상적인 개념을 다루기에 적합하다.
- 그래프를 그려보면 이런 추상적인 개념을 시각화 할 때 도움이 된다. 사회적 관계를 분석할 때 기초가 되기도 한다.
복잡한 문제를 더 간단한 표현으로 단순화하기도 하고 다른 관점으로 표현하여 해결할 수도 있다.
소셜 네트워크, 미디어의 영향, 바이러스 확산 등을 연구하고 모델링 할 때 사용할 수 있다.
- 소셜 네트워크 분석은 데이터 과학에서 그래프 이론을 사용하는 가장 잘 알려진 분야일 것이다. 최근 뉴스에서 코로나19 확산, 이동경로를 나타내고 분석할 때 자주 등장한다. 아래 이미지도 그 중 하나이다.

🏖️ 4. 전통적 그래프 분석 방법의 한계

4.1 알고리즘 기반 방법들

전통적 그래프 분석 방법은 알고리즘에 의존합니다. 대표적인 알고리즘으로는 다음과 같은 것들이 있습니다:
- 검색 알고리즘: BFS(너비 우선 탐색), DFS(깊이 우선 탐색)
- 최단 경로 알고리즘: Dijkstra 알고리즘, A* 알고리즘
- 신장 트리 알고리즘: Prim 알고리즘, Kruskal 알고리즘
- 클러스터링 방법: 연결 성분, 클러스터링 계수 등

4.2 한계

이런 전통적인 방법의 한계는 사전 지식이 필요하다는 점입니다. 즉, 그래프 자체에 대한 연구나 예측이 어렵습니다. 그래프 레벨에서의 예측 작업이 불가능하고, 점이나 선에 대한 세부적인 정보를 다루기에는 적합하지 않습니다.

🏖️ 5. Graph Neural Network(GNN)의 종류와 원리

5.1 Recurrent Graph Neural Network (Recurrent GNN)

Recurrent GNN은 GNN의 가장 기본적인 형태로, Banach Fixed-Point Theorem을 바탕으로 작동합니다.
이 모델은 각 점의 상태를 반복적으로 업데이트하며, 최종 상태를 계산합니다. 점의 상태 업데이트는 점의 이웃 점과 이웃 선의 정보를 기반으로 이루어집니다.

5.2 Spatial Convolutional Network

Spatial Convolutional Network는 CNN(Convolutional Neural Network)의 아이디어를 그래프에 적용한 모델입니다.
CNN이 이미지에서 중심 픽셀 주변의 픽셀 정보를 이용해 학습하는 것처럼, Spatial Convolution은 점의 이웃 점의 특징을 이용해 상태를 업데이트합니다.

5.3 Spectral Convolutional Network

Spectral Convolutional Network는 그래프 신호 처리 이론을 기반으로 하며, 수학적인 기초가 더 강합니다.
이 모델은 인접행렬과 Feature Matrix를 곱하는 방식으로 작동하며, 이를 통해 각 점의 상태가 이웃 점의 상태와 함께 업데이트됩니다.

🏖️ 6. GNN의 주요 응용 사례

6.1 Node Classification (노드 분류)

Node Classification은 그래프의 각 점을 분류하는 문제입니다.
주로 semi-supervised learning을 사용하여 일부 점들만 레이블이 부여된 상황에서 학습합니다. 인용 네트워크나 Reddit 게시물, Youtube 동영상 분류와 같은 문제에서 응용됩니다.

6.2 Link Prediction (링크 예측)

Link Prediction은 두 점 사이의 관계를 예측하는 문제입니다. 예를 들어, 페이스북 친구 추천이나 영상 추천 시스템에서 두 점(유저-영화)이 연결될 가능성을 예측할 수 있습니다.

6.3 Graph Classification (그래프 분류)

Graph Classification은 그래프 전체를 하나의 카테고리로 분류하는 문제입니다. 분자 구조 분석과 같은 문제에서 많이 사용되며, 화학이나 생명공학 연구에서 활발히 응용됩니다.

🏖️ 7. GNN의 실제 활용 사례

7.1 Scene Graph Generation

Scene Graph Generation은 이미지에서 물체 간 관계를 분석하여 scene graph를 생성하는 작업입니다. CNN을 기반으로 물체들을 탐지한 후, GNN을 사용하여 그들 간의 관계를 그래프로 나타낼 수 있습니다.

7.2 Image Generation from Scene Graphs

Scene Graph로부터 이미지를 생성하는 작업도 가능합니다. 기존의 Generative Adversarial Network (GAN)이나 Autoencoder와는 다른 방법으로, GNN을 활용하여 이미지를 생성할 수 있습니다.

7.3 Graph-Structured Representations for Visual Question Answering

Visual Question Answering (VQA) 문제에도 GNN을 도입하여 성능을 향상시킬 수 있습니다. 장면과 질문으로부터 각각 scene graph와 question graph를 생성하고, 이를 통해 더 나은 응답을 제공합니다.

7.4 Machine Learning for Scent

머신러닝과 GNN을 활용하여 분자 구조를 분석하고 향을 예측하는 작업도 가능합니다. 기존에 분자 구조 분석에 사용되던 Mordred나 Fingerprint 방법을 넘어, GNN으로 분자 구조의 특징을 추출하여 향을 예측할 수 있습니다.

7.5 Graph Convolutional Matrix Completion

Graph Convolutional Matrix Completion은 유저-영화 평점 행렬을 기반으로, 평가되지 않은 유저-영화 쌍에 대해 예상 평점을 계산하는 방법입니다. 이를 통해 개인화된 추천 시스템을 구현할 수 있습니다.

🏖️ 8. 결론 및 마무리

GNN은 여전히 새로운 분야이지만, 그래프 데이터를 분석할 때 매우 유용한 방법입니다. GNN은 다른 머신러닝 기법들과는 달리, 점들 간의 관계를 모델링하여 더 논리적인 학습 과정을 제공합니다.
그래프 이론을 응용하는 다양한 분야에서 GNN이 차지하는 역할이 커지고 있으며, 앞으로도 화학, 생명과학, 소셜 네트워크 분석 등 여러 도메인에서의 확장이 기대됩니다.

🏖️ 9. 참고자료

Scarselli, F., Gori, M., “The Graph Neural Network Model,” IEEE Transactions on Neural Networks, 2009.
Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., Philip S. Yu, “A Comprehensive Survey on Graph Neural Networks,” arXiv:1901.00596.
Kipf, T. N., & Welling, M., “Semi-Supervised Classification with Graph Convolutional Networks,” ICLR, 2017.
Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O., Dahl, G. E., “Neural Message Passing for Quantum Chemistry,” ICML, 2017.
Xu, D., Zhu, Y., Choy, C. B., & Fei-Fei, L., “Scene Graph Generation by Iterative Message Passing,” CVPR, 2017.
Johnson, J., Gupta, A., & Fei-Fei, L., “Image Generation from Scene Graphs,” CVPR, 2018.
Teney, D., Liu, L., & Hengel, A. van den, “Graph-Structured Representations for Visual Question Answering,” CVPR, 2017.
Sanchez-Lengeling, B., Wei, J. N., Lee, B. K., Gerkin, R. C., Aspuru-Guzik, A., & Wiltschko, A. B., “Machine Learning for Scent: Learning Generalizable Perceptual Representations of Small Molecules,” arXiv:1910.10685.
van den Berg, R., Kipf, T. N., & Welling, M., “Graph Convolutional Matrix Completion,” arXiv:1706.02263.

참고 자료

medium GNN 소개

이영락

AI Engineer / 의료인공지능

이전 포스트

추천시스템 (2) gnn 개요

인공지능 공부