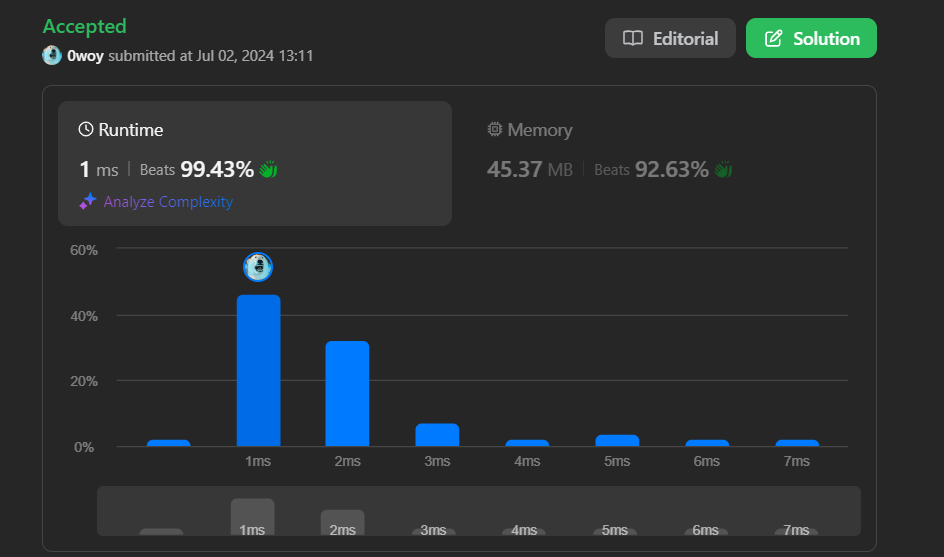
📜 문제
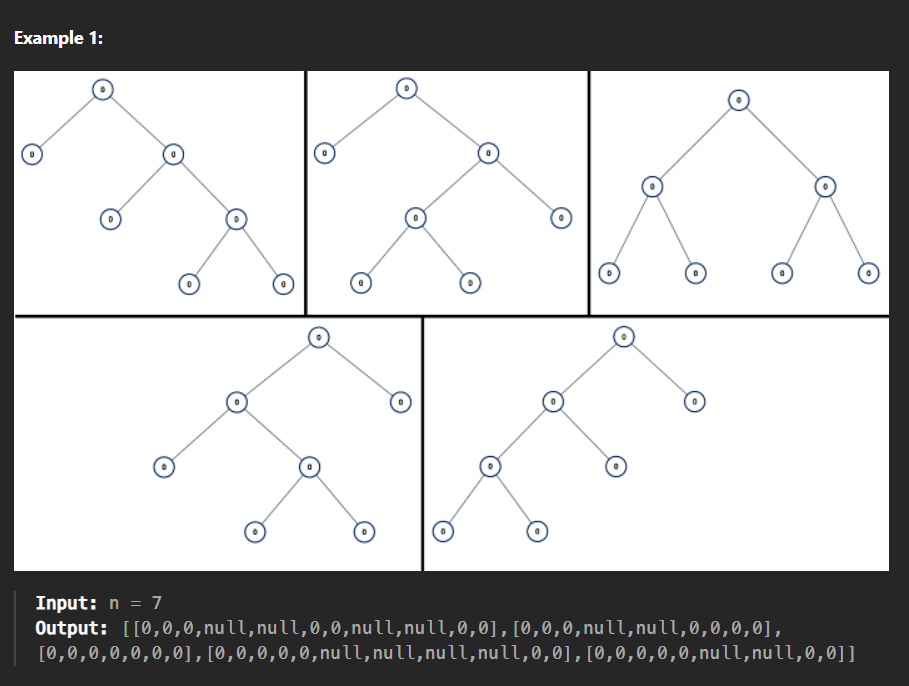
- 정수 n이 주어질 때, n개의 노드를 갖는 완전 이진 트리의 모든 경우 를 반환하라.
❓ 문제에 제시된 완전 이진 트리(Full Binary Tree)
모든 노드의 자식 노드가
0개이거나2개인 트리
접근
dp 문제인 것도 알았고, 규칙은 찾았은 것 같았지만.. 손대기 쉽지 않았다
왜냐하면 내가 모자라기 때문이다.
내가 찾은 규칙은 이렇다
1. N개의 노드를 갖는 FBT
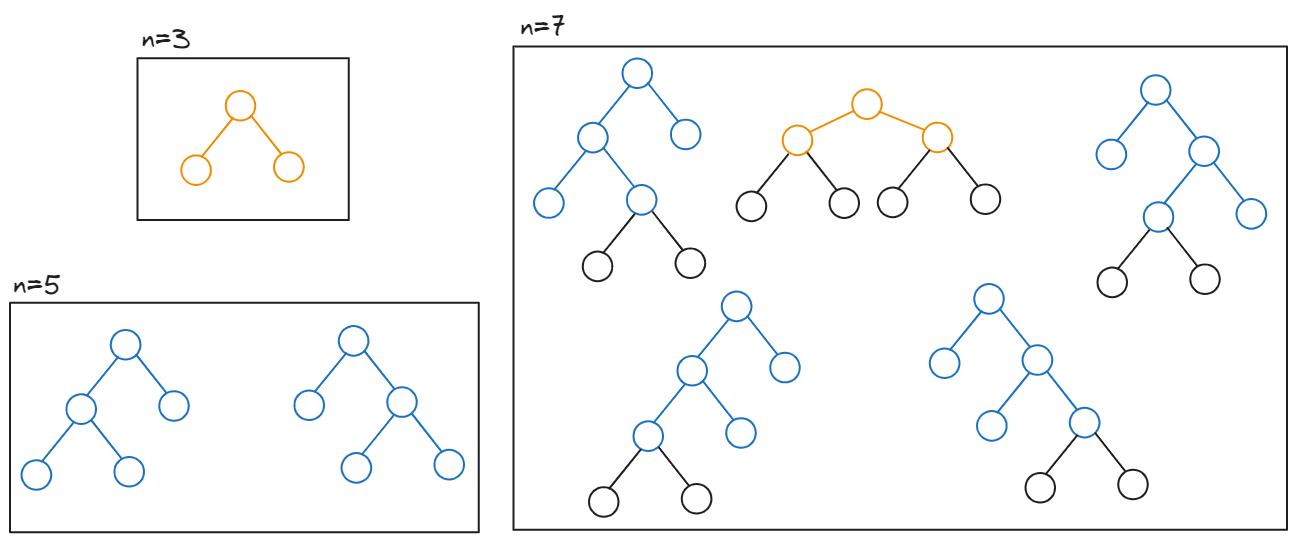
n=3, 5, 7일 때 모든 완전 이진 트리를 나열한 그림이다.
그림을 보면 n=7일 때, n=5와 n=3인 FBT에서 노드가 추가됐다고 볼 수 있다.
그렇다면 완전 이진 트리를 만들 되, n개의 노드로 만들 수 있는 FBT를 저장해 두면 불필요한 중복을 줄일 수 있겠다.
2. FBT의 조건
모든 노드의 자식노드는 0개이거나 2개여야 한다.
그렇다면 왼쪽 서브트리, 오른쪽 서브트리가 갖는 노드 수는 홀수여야한다.
사유. 부모 노드를 포함하여 계산 돼야 하기 떄문.
짝수인 경우 위 완전 이진트리 조건을 충족할 수 없다.
코드를 함 뜯어보자

🍳 전체 소스 코드
class Solution {
private static Map<Integer, List<TreeNode>> dp = new HashMap<>();
public List<TreeNode> allPossibleFBT(int n) {
if(dp.containsKey(n)){
return dp.get(n);
}
if(n==1){
List<TreeNode> single = new ArrayList<>();
single.add(new TreeNode(0));
return single;
}
List<TreeNode> res = new ArrayList<>();
for(int i=1;i<n;i+=2){
List<TreeNode> leftTree = allPossibleFBT(i);
List<TreeNode> rightTree = allPossibleFBT(n-i-1);
for(TreeNode left: leftTree){
for(TreeNode right: rightTree){
TreeNode root = new TreeNode(0,left, right);
res.add(root);
}
}
}
dp.put(n, res);
return res;
}
}- dp 변수
key: n개의 노드
value: 노드 n개 가 가질 수 있는 완전 이진 트리
1) dp에 n개의 노드로 만들 수 있는 FBT가 있는 경우 바로 반환한다.
2) n이 1인 경우
노드 1개이므로 노드 1개를 담은 single 리스트를 반환한다.
3) 그 외의 경우
총 n-1개의 노드를 왼쪽 서브트리, 오른쪽 서브트리가 노나 가져야 한다.
예시)
n=5일 때,
i=1~4까지
왼쪽 서브트리 노드 1개 - 오른쪽 서브트리 노드 3개
왼쪽 서브트리 노드 3개 - 오른쪽 서브트리 노드 1개
이런식이다.? 왜 2일 때랑 4일 때는 안 봐요!?!!@#!@#
--> 그러면 완전 이진트리 못 만든다고. 설명했어요.
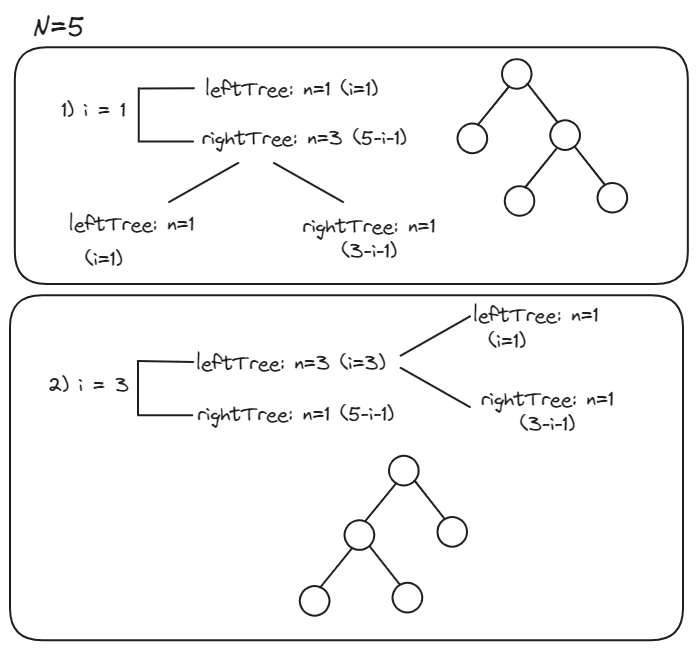
n=5인 경우 위와 같은 경우의 수가 나온다.
✨ 결과
어려웠다.
재귀도 어렵고.. dp도 어렵다.. 둘이 합쳐놓으니까 두 배로 어렵다!
디버깅하면서 하나씩 뜯어보면 훨씬 이해가 쉬울 것이다.