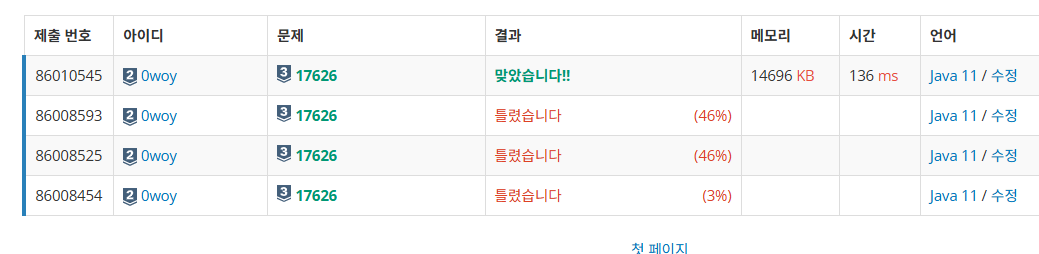
📜 문제
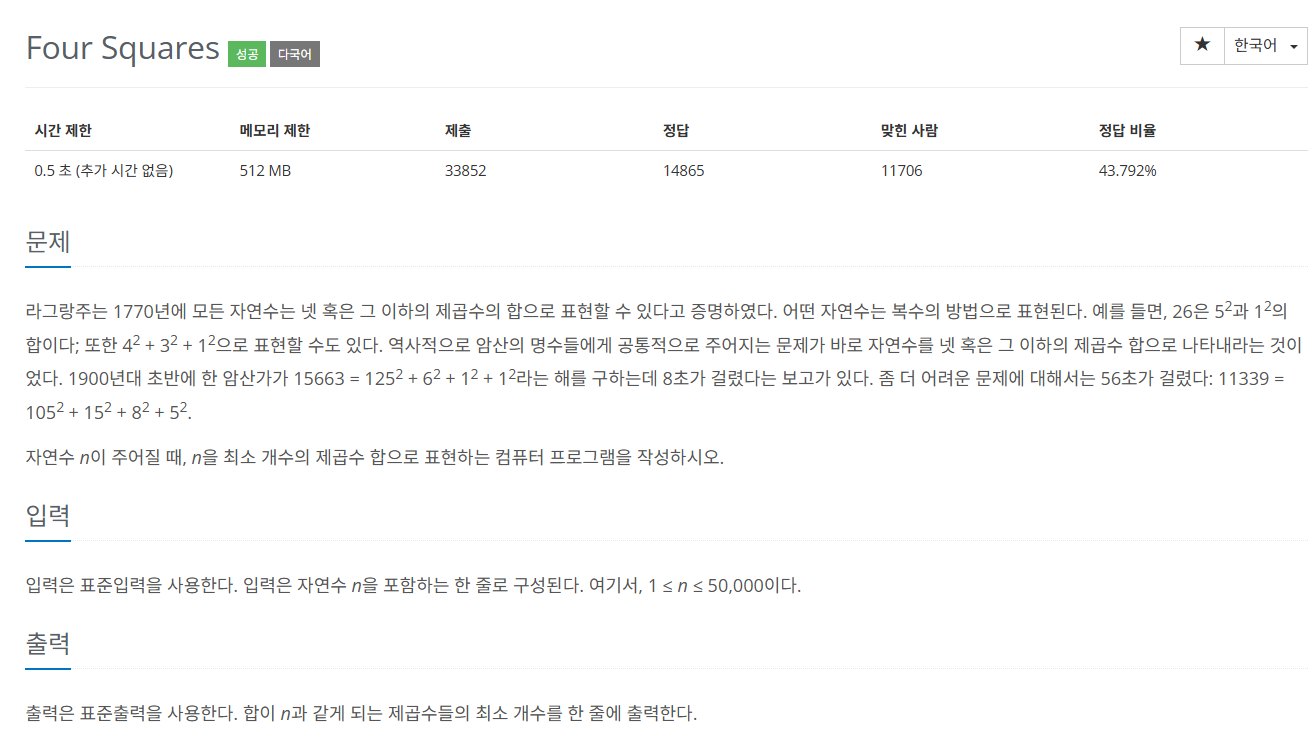
모든 자연수는 4개 이하의 제곱수의 합으로 표현 가능.
어떤 자연수는 해당 제곱수의 합이 여러개일 수도 있다.
- 어떤 자연수가 주어질 때, 표현되는 제곱수가 가장 적은 개수 찾아라.
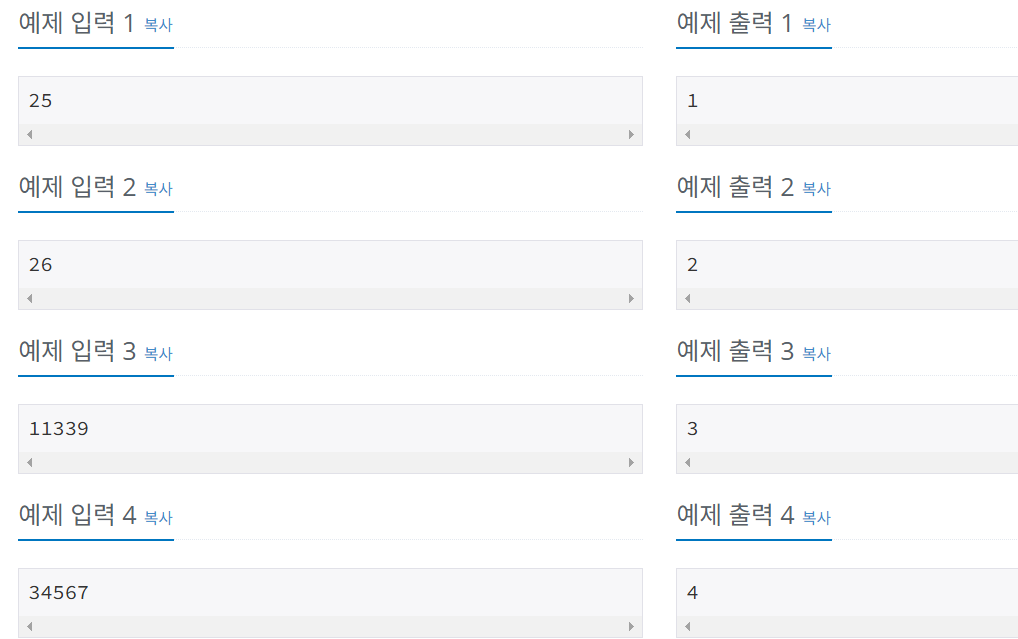
ex) N = 26
5²+1²: 2개
4²+3²+1²: 3개
답: 2개
생각하기
틀렸어요. 답 봤구요..
처음엔 그리디인줄 알고 풀었는데 그리디가 아니었다.
내가 접근한 방식을 잠깐 설명하자면,
- 처음 주어지는 자연수
(이하 n)의 제곱근(이하 sqrt)찾기 (소수점 내림).- n에서 sqrt² 뺀 값을 n에 저장. (n = n-sqrt²)
n이 0이 될 때까지 위 과정을 반복.
이렇게 풀고 제출했는데, 46%에서 틀렸다.
반례는 27532 자연수가 들어왔을 때 나왔다.
답은 27532 = 26²+ 66² + 150²로 3개가 나와야 한다.
나의 로직은 아래와 같은 계산 과정으로 제곱수 개수를 구한다.
| 계산 과정 | 계산 결과 |
|---|---|
| √27532 | = 165.92... |
| 27532 - 165² | = 307 |
| √307 | = 17.52.. |
| 307 -17² | = 18 |
| √18 | = 4.24... |
| 18 - 4² | = 2 |
| 2 | = 1²+1² |
27532 = 1²+1²+4²+17²+165² 로 가장 작은 개수도 아닐 뿐더러 4개를 초과한다. ㅋㅋ
그래서 가장 큰 값만 취하는 그리디 방식이 답이 아님을 알게 됐다...
그리디만 철썩 같이 믿었는데.. ㅜ
아무튼 다른 분들의 풀이를 봤다.
접근 방식
브루트 포스로 풀 수도 있고, dp로 풀 수 있다고 한다.
dp가 훨씬 효율적이기에 dp 풀이를 참고했다.
| n | 최소 제곱근 개수 |
|---|---|
| 1 | 1개 (1²) |
| 2 | 2개 (1²+1²) |
| 3 | 3개 (1²+1²+1²) |
| 4 | 1개 (2²) |
| 5 | 2개 (2²+1²) |
앞서 말했듯 n은 √n 이하의 제곱수들의 합으로 구성이 된다.
n이 4인 경우를 예로들자.
- 1²+1²+1²+1²
- 2²
위 처럼 표현이 가능한데, 우리는 2²을 취해야 한다.
그런데,1²+1²+1²+1²은 3의 제곱수합에서 1²을 더한 값이다.
그러면 1부터 x²<=n일 때까지 x를 증가해 나가면서 가장 적은 개수를 저장하면 되나?
라고 생각할 수 있는데, 처음 보면 뭔 소리인지 싶다.
dp 배열에 해당 자연수에 대한 최소 값들이 저장돼 있다고 가정해 보자.
n=4,
idx = 4-1² => dp[3]
idx = 4-2² => dp[0]
dp[3]과 dp[0]중 가장 적은 친구를 취해서 +1 하면,
그게 4를 만들 수 있는 가장 적은 개수라는 말이다.
3을 만들 수 있는 최소 제곱수 개수는 3개이고(1²+1²+1²),
0을 만들 수 있는 최소 제곱수는 0개이므로 우리는 0을 택한다.
그렇게 하면 dp[4]=1이므로 옳게 나온다.
16을 예로 들면, 아래 경우 중 최소 값을 취하여 저장한다.
16-1² = 15.
(dp[15])+1개
16-2² = 12(dp[12])+1개
16-3² = 7(dp[7])+1개
16-4² = 0(dp[0])+1개
이해가 됐으면 좋겠다ㅠ
🍳 전체 소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main{
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for(int i=2;i<=n;i++){
int min = Integer.MAX_VALUE;
for(int j=1;j*j<=i;j++){
min = Math.min(min,dp[i-j*j]);
}
dp[i] = min+1;
}
System.out.println(dp[n]);
}
}- 최소 개수를 저장하는 dp 배열을 선언 & 초기화
- dp[0]과 dp[1]에는 값 미리 저장
- 최소 개수 저장
- i는 2부터 n까지
- j는 1부터 j*j <= i 까지 반복.
- 제일 적은 개수를 min에 저장
- 최종적으로 찾은
min에 1을 더한 값을dp[i]에 저장
dp[n]출력
✨ 결과
진짜 알다가도 모를.. 아니 그냥 모르는 dp...
해당 문제 북마크 해두고 한 달 뒤에나 한 번 더 풀어봐야겠다.
이번 문제 설명하기 넘 어려웠다. 하지만 최선은 다했다 ㅎ