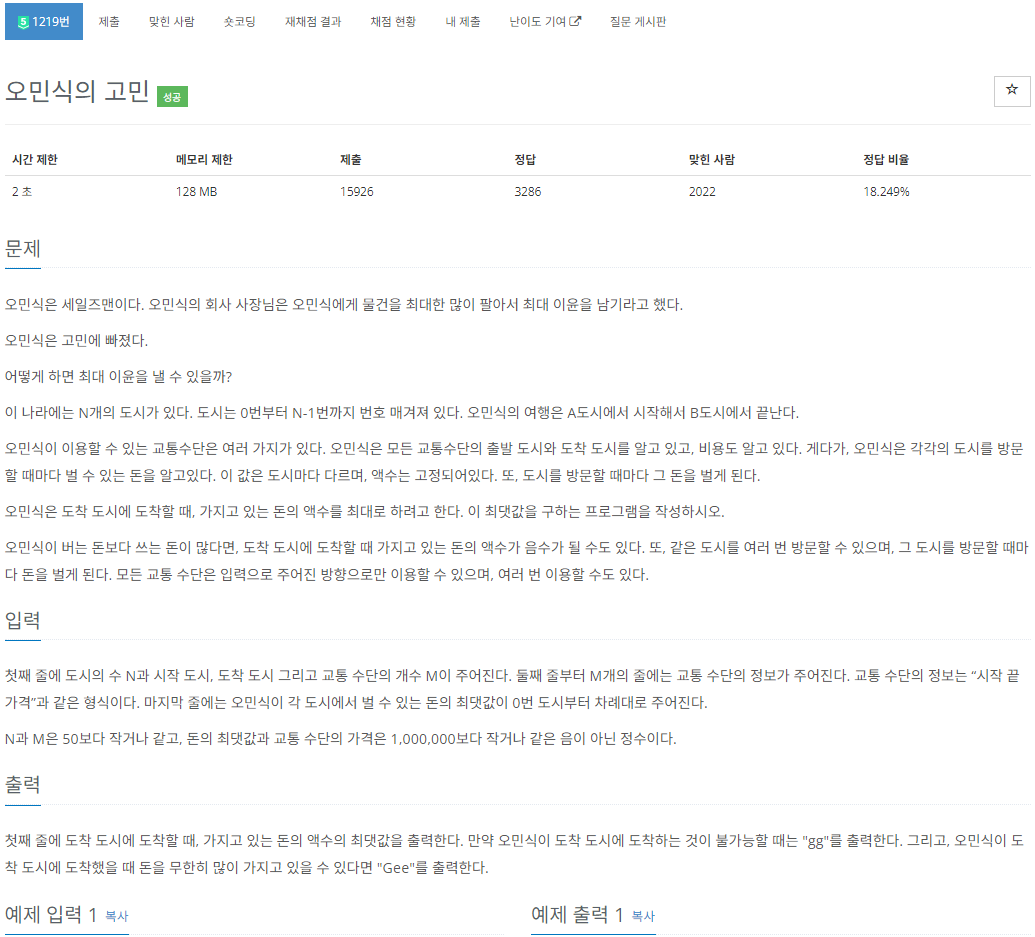
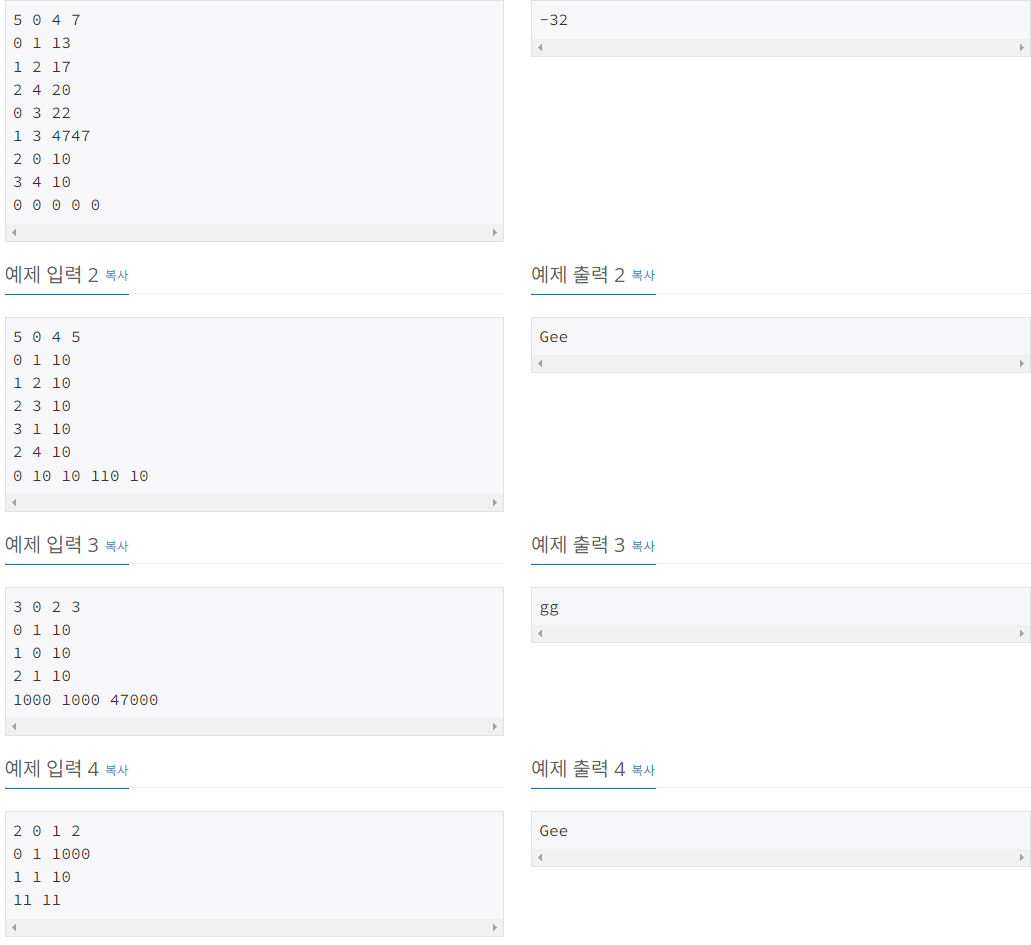
문제사항

플래티넘 5단계 문제였다.

일반적인 벨만-포드는 N-1까지 최단 경로를 업데이트 한 뒤 마지막으로 한번 반복하여 사이클 여부를 여부를 판단한다.

하지만 이 문제에서는 오민식이 벌 수 있는 돈이 무한대 라고 언급한다.

이는 양의 사이클이 발생하며 (=최대 거리를 구하며) 양의 사이클인지 음의 사이클인지 판단하라는 뜻이다.

계속해서 벨만-포드 문제를 풀며 최단 경로를 업데이트 했으나, 여기선 최대 거리를 구해야 한다.

키 포인트

• 각 도시에서 돈을 벌 수 있다.
• 도시 간 이동에는 비용이 든다.
• 같은 도시를 여러 번 방문 가능하다.
• 양의 사이클 (=계속 돈을 벌 수 있는 루트)이 존재할 수 있다.

자료구조

• Edge[]: 각 교통 수단(간선)의 정보를 저장
• long[] dist: 각 도시까지의 최대 이익을 저장
• long[] money: 각 도시에서 벌 수 있는 돈을 저장

** int 범위를 넘을 수 있으므로 long을 사용

벨만-포드 알고리즘 변형

• 초기에 모든 도시의 이익을 최소값으로 설정
• N+50번 반복하여 각 간선을 확인하고 이익을 갱신
  => 최댓값인 N+50번 정도의 충분한 반복으로 모든 가능한 경로를 고려
• 양의 사이클 검출: N번 이상 반복 후에도 이익이 증가하면 무한대로 설정

알고리즘 분류

그래프 (벨만 포드)

코드

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());  // 도시의 수
        int start = Integer.parseInt(st.nextToken());  // 시작 도시
        int destination = Integer.parseInt(st.nextToken());  // 도착 도시
        int M = Integer.parseInt(st.nextToken());  // 교통 수단의 개수

        Edge[] grape = new Edge[M + 1];  // 교통 수단(간선) 정보를 저장할 배열
        long[] dist = new long[N + 1];  // 각 도시까지의 최대 수익을 저장할 배열

        // 교통 수단 정보 입력
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());  // 출발 도시
            int b = Integer.parseInt(st.nextToken());  // 도착 도시
            int c = Integer.parseInt(st.nextToken());  // 교통 비용
            grape[i] = new Edge(a, b, c);
        }

        // 각 도시에서 벌 수 있는 돈 입력
        long[] money = new long[N + 1];
        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < N; i++) {
            money[i] = Integer.parseInt(st.nextToken());
        }

        // 벨만 포드 알고리즘 시작
        Arrays.fill(dist, Long.MIN_VALUE);  // 모든 도시의 초기 수익을 최소값으로 설정
        dist[start] = money[start];  // 시작 도시의 수익 초기화

        // N+50번 반복 (양의 사이클 검출을 위해 충분히 큰 횟수로 설정)
        for (int i = 0; i <= N + 50; i++) {
            for (int j = 0; j < M; j++) {
                Edge now = grape[j];
                // 출발 도시에 도달할 수 없는 경우 스킵
                if (dist[now.st] == Long.MIN_VALUE) {
                    continue;
                }
                // 출발 도시가 양의 사이클에 포함된 경우, 도착 도시도 무한대 수익으로 설정
                else if (dist[now.st] == Long.MAX_VALUE) {
                    dist[now.end] = Long.MAX_VALUE;
                }
                // 수익이 증가하는 경우 업데이트
                else if (dist[now.end] < dist[now.st] + money[now.end] - now.cost) {
                    dist[now.end] = dist[now.st] + money[now.end] - now.cost;
                    // N번 이상 반복했을 때 여전히 업데이트가 발생하면 양의 사이클로 판단
                    if (i >= N) {
                        dist[now.end] = Long.MAX_VALUE;
                    }
                }
            }
        }

        StringBuilder sb = new StringBuilder();
        // 도착 도시에 도달할 수 없는 경우
        if (dist[destination] == Long.MIN_VALUE) {
            sb.append("gg").append("\n");
        }
        // 도착 도시가 양의 사이클에 포함된 경우
        else if (dist[destination] == Long.MAX_VALUE) {
            sb.append("Gee").append("\n");
        }
        // 정상적으로 도착 도시에 도달한 경우
        else {
            sb.append(dist[destination]).append("\n");
        }
        System.out.println(sb);
    }

    // 간선(교통 수단) 정보를 저장하는 클래스
    static class Edge{
        int st;  // 출발 도시
        int end;  // 도착 도시
        int cost;  // 비용

        public Edge(int st, int end, int cost) {
            this.st = st;
            this.end = end;
            this.cost = cost;
        }
    }
}