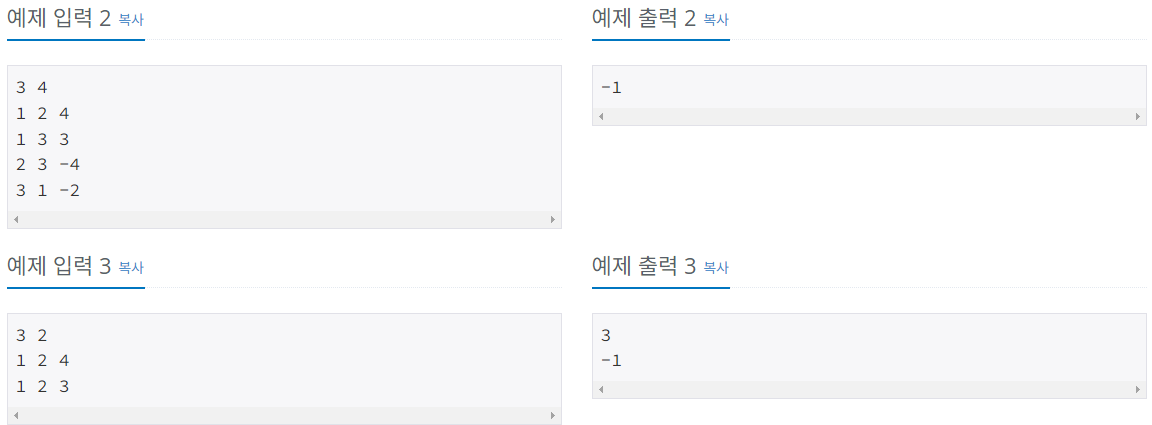
문제사항
골드 4단계 문제였다.
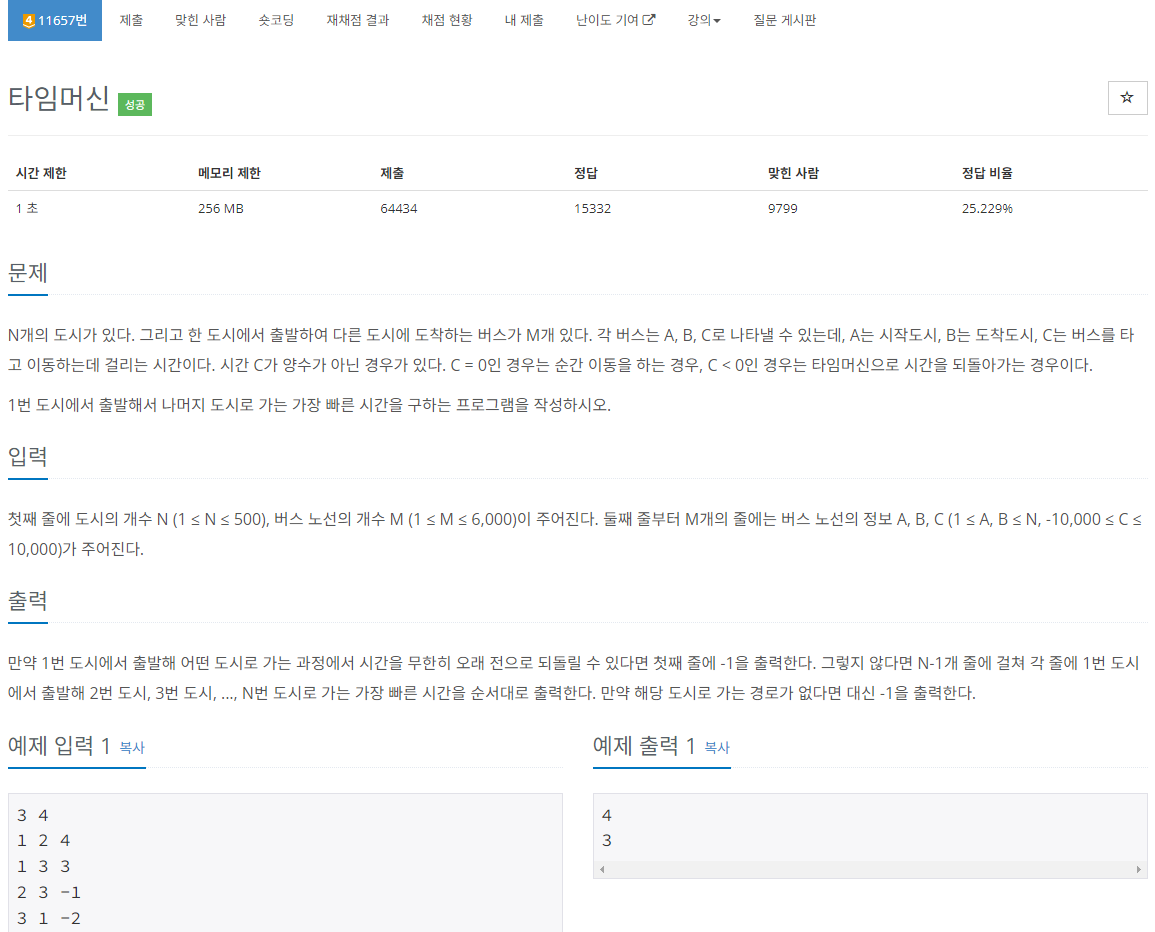
문제를 읽어보면 1번도시부터 N번 도시로 가는 가장 빠른 시간을 구해야 하며, 여기선 도시 간 이동하는데 있어 가중치가 있다.
시작 도시(노드)가 주어지고, 음의 가중치를 가진 엣지가 존재한다.
위 문제는 음수 사이클까지 판단해야되기 때문에 벨만-포드 알고리즘을 사용해야 한다.
그렇다면 벨만-포드 알고리즘이 무엇인지 알아보자.
'벨만-포드' 란?
그래프에서 최단 거리를 구하는 알고리즘은 다익스트라, 벨만포드, 플로이드 워셜이 있다.
다익스트라는 직전 포스팅에서 이론을 학습하고, 총 3개의 백준 문제를 풀었었다. 다익스트라가 무슨 알고리즘이고, 어떤 유형으로 출제되는지 궁금하다면 다음 포스팅을 참고하자.
벨만-포드는 특정 출발 노드(=시작점 존재)에서 다른 모든 노드의 최단 경로 탐색을 요구한다.
여기서 특징은 음수 간선이 존재하여, 음수 사이클의 존재 여부를 판단할 수 있다.
이때 시간 복잡도는 O(VE)이다.
1. ”에지 리스트” 로 그래프를 구현하고 최단 경로 리스트 초기화
에지를 중심으로 동작함으로 그래프를 에지 리스트로 구현한다.
최단 경로 리스트는 출발노드는 0, 나머지 노드는 무한대로 초기화한다.
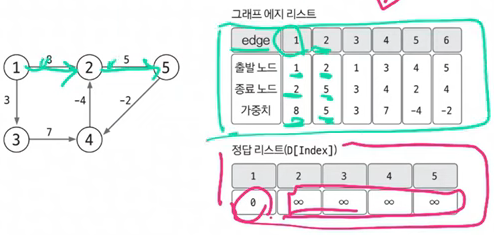
2. 모든 에지를 확인해 정답 리스트 업데이트하기
업데이트 반복 횟수는 노드 개수 -1이다.
노드의 개수가 N, 음수 사이클이 없다면 특정 두 노드의 최단거리를 구성할 수 있는 에지의 최대 개수는 N-1이기 때문이다.
모든 에지 E = ( s, e, w )에서 다음 조건을 만족하면 새 업데이트를 실행한다.
[업데이트 조건과 방법]
D[s] != 무한대이며 D[s] + w < D[e]일 때 D[e] = D[s] + w로 리스트 값 업데이트
업데이트 반복 횟수가 K번이면, 해당 시점에 정답 리스트의 값은 시작점에서 K개의 에지를 사용했을 때 각 노드에 대한 최단 거리를 구할 수 있다.
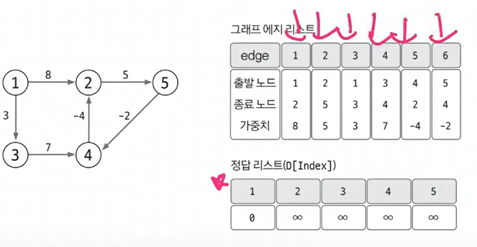
- 처음에는 모든 에지를 다 검토
- 이때 출발 노드(=1)는 무한대가 아니여야 한다.
[ 시작 노드에서 1개의 에지를 사용 ]
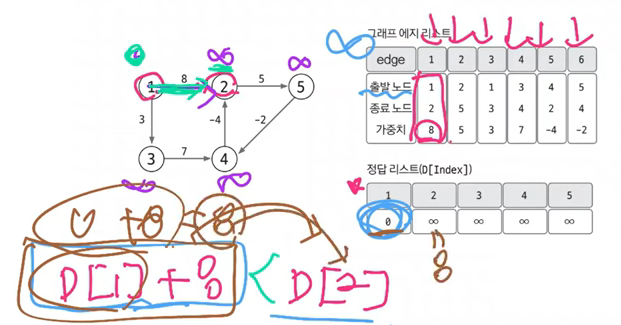
- 1에서 2로 가는데 가중치 8이 있다.
- D[1] + 8 < D[2]
- 0+8<무한대 이므로 새로 들어온 D[1]+8이 더 작다.
- 따라서 더 작은 값을 D[2]에 대입해준다.
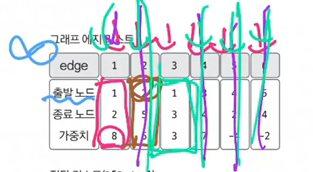
- 이처럼 업데이트를 시작할 수 있는 노드는 1밖에 없다.
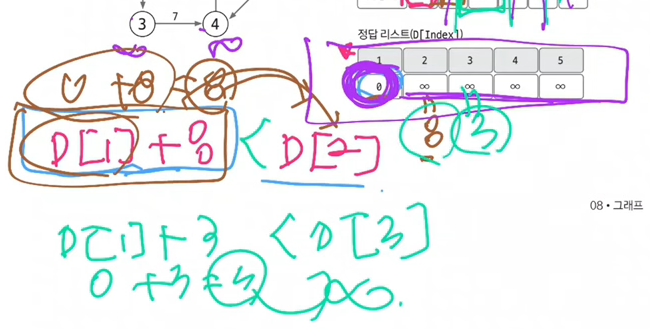
- 그러므로 1에서 3으로 이동하는 에지도 업데이트 시킬 수 있다.
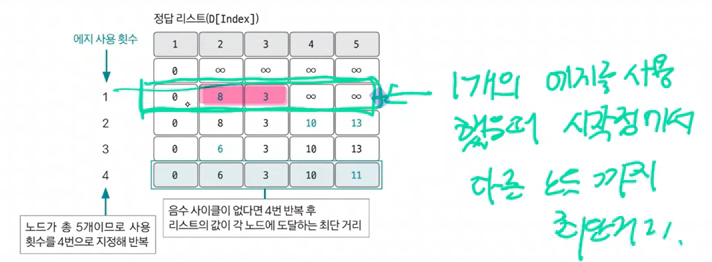
[ 시작 노드에서 2개의 에지를 사용 ]
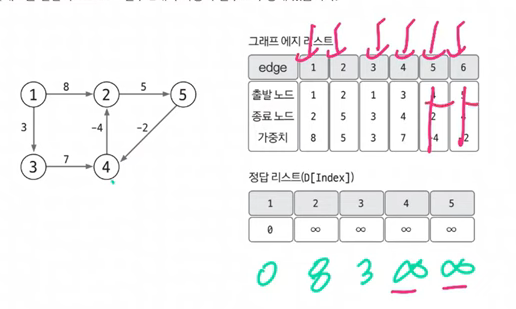
- 에지 4,5는 이미 무한대기 때문에 조건에서 제외됨
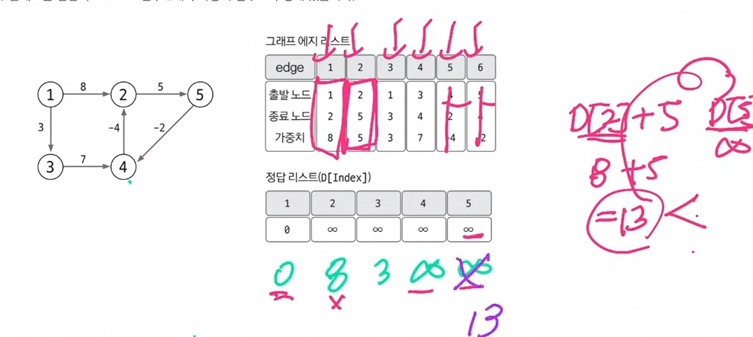
- D[2] + 5 < D[5] 조건에 부합하므로 D[5]는 8+5=13을 대입
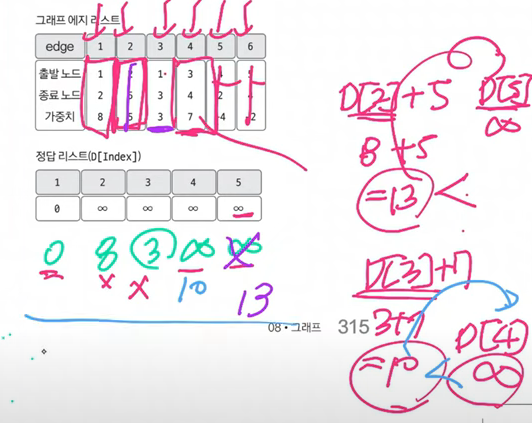
- D[3] + 7 < D[4] 조건에 부합하므로 D[4]는 3+7=10을 대입
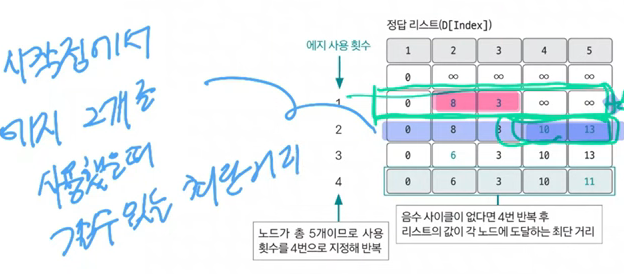
[ 노드의 개수가 5개므로 4번까지 업데이트를 반복 ⇒ 최단거리 완성 ]
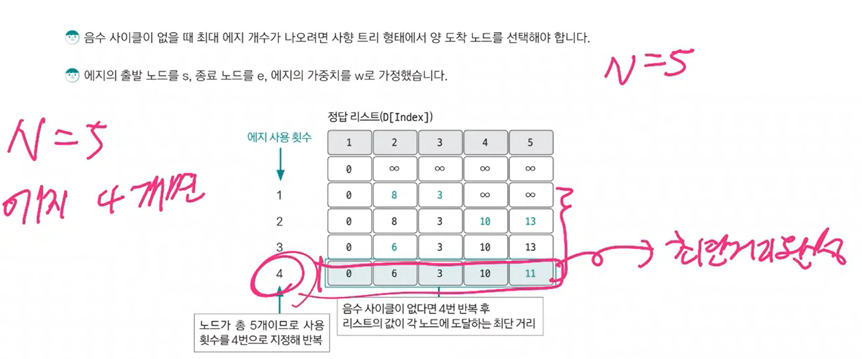
그러나..
벨만포드는 음수 사이클이 있는지 찾는 문제가 많이 나온다!
- 음수 사이클이 없을때 N-1번 에지 사용 횟수를 반복하면 출발 노드와 모든 노드 간의 최단 거리를 알려 주는 정답 리스트가 완성
⇒ 마지막으로 이 그래프에 음수 사이클이 존재하는지 확인
3. 음수 사이클 유무 확인하기
- 모든 에지를 한 번씩 다시 사용해 업데이트 되는 노드가 발생하는지 확인
- 만약 업데이트 되는 노드가 있다면 음수 사이클이 있다는 뜻
- 음수 사이클 존재하면 이 사이클을 무한하게 돌수록 가중치가 계속 감소하여 최단거리 구할 수 없음
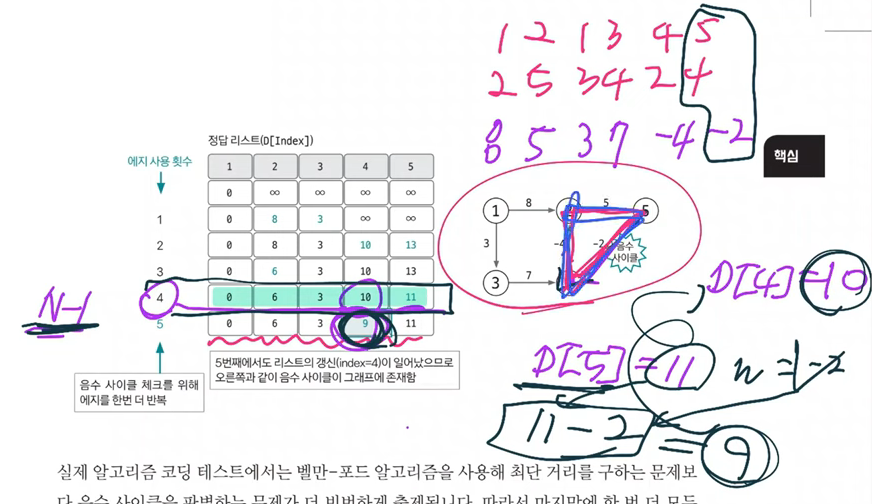
-
D[5]-2 < D[4]를 계산해보면 11-2< 10이기 때문에 업데이트 조건에 부합한다.
-
N-1번을 사용해서 최단거리가 나왔는데 한번 더 했을 때 업데이트가 되었다는 것은 “음수 사이틀이 있다는 뜻”
⇒ 해당 그래프는 최단 거리를 구할 수 없는 그래프이다.
알고리즘 분류
그래프 (벨만-포드 알고리즘)
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
// 에지리스트
Edge[] edges = new Edge[M + 1];
// 정답배열(최단거리 배열)
long[] D = new long[N + 1];
Arrays.fill(D, Integer.MAX_VALUE);//dist 배열의 모든 요소를 Integer.MAX_VALUE로 초기화
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int C = Integer.parseInt(st.nextToken());
edges[i] = new Edge(A, B, C);
}
// 벨만 포드
D[1] = 0; // 시작노드는 0
for (int i = 1; i < N; i++) { // 업데이트 반복 횟수: N-1
for (int j = 0; j < M; j++) {
Edge edge = edges[j];
if (D[edge.start] != Integer.MAX_VALUE && D[edge.start] + edge.cost < D[edge.end]) {
D[edge.end] = D[edge.start] + edge.cost; // 업데이트
}
}
}
// 음수 사이클 판별 ( 한번 더 수행 )
boolean check = false;
for (int i = 0; i < M; i++) {
Edge edge = edges[i];
if(D[edge.start] != Integer.MAX_VALUE && D[edge.start] + edge.cost < D[edge.end]){
check = true;
}
}
StringBuilder sb = new StringBuilder();
if (check) { //음수 사이클이 존재한다면
sb.append("-1");
} else { //음수 사이클이 존재하지 않다면
//D[1]은 0이므로 2부터 시작
for (int i = 2; i <= N; i++) {
if (D[i] == Integer.MAX_VALUE) {
sb.append("-1").append("\n");
} else {
sb.append(D[i]).append("\n");
}
}
}
System.out.println(sb);
}
static class Edge {
int start;
int end;
int cost;
public Edge(int start, int end, int cost) {
this.start = start;
this.end = end;
this.cost = cost;
}
}
}
