문제사항

실버 1단계 문제였다.

[백준] 1219번 오민식의 고민 (JAVA) 문제와 마찬가지로 플로이드-워셜 문제이다.

플로이드-워셜 알고리즘에 대해 궁금하다면 위 포스팅을 참고하자.

플로이드-워셜의 핵심이론은 다음과 같다.

A 노드에서 B 노드까지 최단 경로를 구했다고 가정했을 때 최단 경로 위에 K 노드가 존재한다면 그것을 이루는 부분 경로 역시 최단 경로이다.

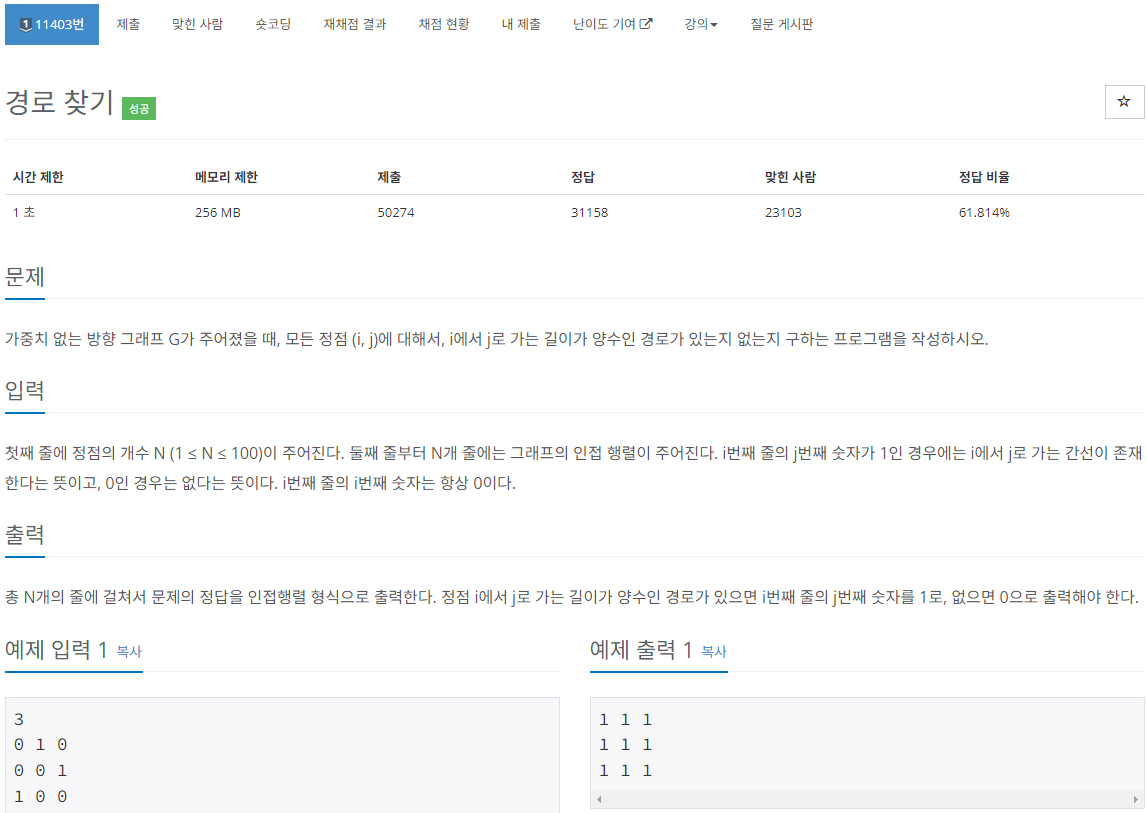
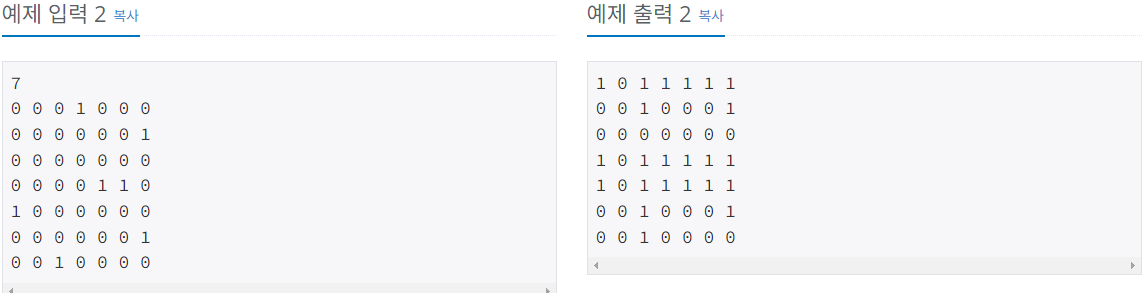
가만보면 위 문제에서 i번째 줄의 j번째 숫자가 1인 경우에는 i에서 j로 가는 간선이 존재한다는 뜻이고, 0인 경우는 없다는 뜻이다. 라고 언급하고 있다.

문제에서는 i에서 j로 갈 수 있는 경로가 있는지 판단해 인접행렬로 출력을 요구하고 있다.

이는 플로이드 핵심원리와 똑같다는 것을 간접적으로 말하고 있다.

따라서 거쳐가는 정점이 k라고 할때 D[i][k] == 1 그리고 D[k][i] == 1이라는 두 조건 모두 부합하다면 D[i][j] = 1 이라고 할 수 있다.

알고리즘 분류

그래프 (플로이드-워셜)

코드

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        int N = Integer.parseInt(br.readLine());
        int[][] D = new int[N + 1][N + 1];

        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 0; j < N; j++) {
                D[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        //플로이드-워셜
        for (int k = 0; k < N; k++) {
            for (int i = 0; i < N; i++) {
                for (int j = 0; j < N; j++) {
                    if (D[i][k] == 1 && D[k][j] == 1) {
                        D[i][j] = 1;
                    }
                }
            }
        }

        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                sb.append(D[i][j]).append(" ");
            }
            sb.append("\n");
        }
        System.out.println(sb);
    }
}