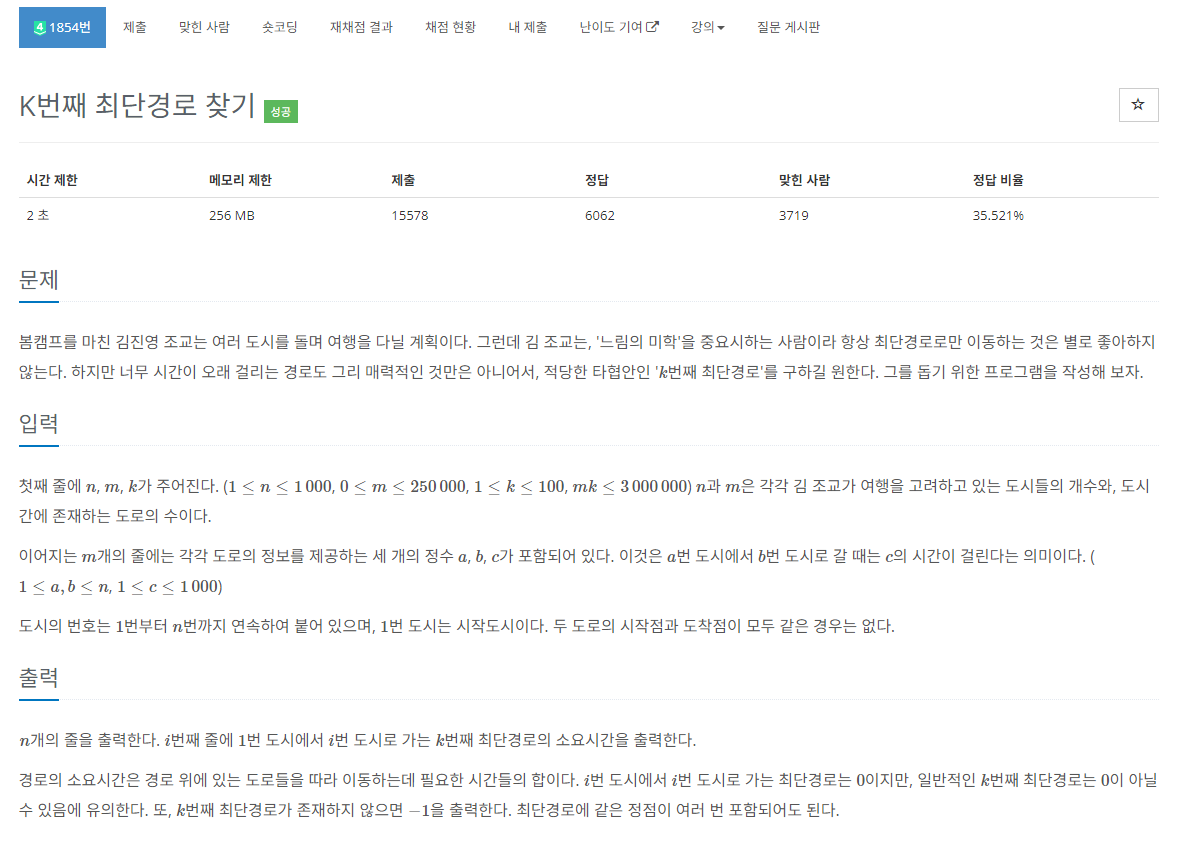
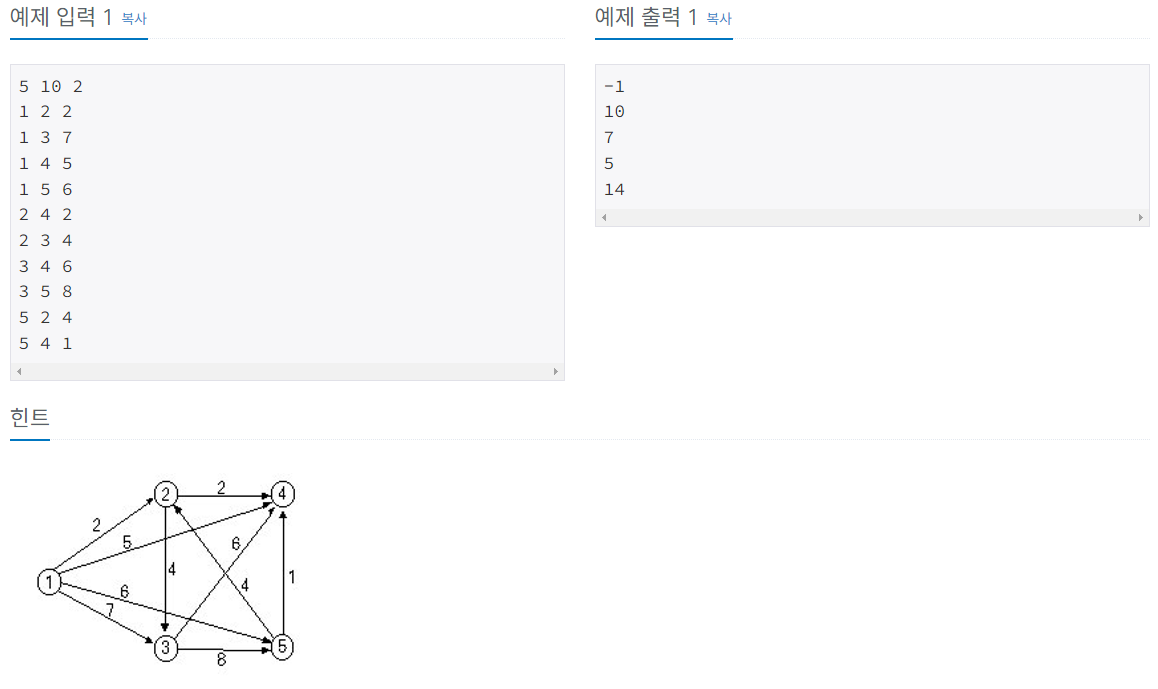
문제사항

플래티넘 4단계 문제였다.

[백준] 1753번 최단경로(JAVA)와 [백준] 1916번 최소비용 구하기(JAVA) 문제와 마찬가지로 다익스트라 알고리즘 문제이다.

일반적인 다익스트라는 최소 거리를 구해 도출하면 됐었지만, 이 문제는 k개의 최단 거리를 구해야한다.

기존에 int[] D = new int[V + 1];로 선언했던 1차원 int형 배열로 사용하면 안된다.
따라서 우선순위큐 배열을 사용한다. PriorityQueue<Integer>[] distQue = new PriorityQueue[n + 1];

문제에서 k개의 최단거리를 구하라고 하였기 때문에 모든 최단거리를 저장할 필요 없다.
주어진 k개의 최단거리만 저장하자.

만약 우선순위큐 배열에 k개보다 작은 최단거리가 저장되어 있다면 새로운 경로를 다익스트라 알고리즘으로 저장한다.

우선순위큐 배열은 Comparator를 적용하여 사용하는 비교자를 커스터마이징하였기 때문에 자동으로 정렬된다.

k개 이상 최단거리가 저장되어 있는데 새로운 경로가 발생하면 우선순위큐 배열에 저장되어 있는 가장 큰 값보다 작으면 가장 큰 값을 꺼내서 삭제하고, 새로운 경로를 추가해주었다.

알고리즘 분류

그래프 (다익스트라)

코드

import java.io.*;
import java.util.*;
public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken()); //노드
        int m = Integer.parseInt(st.nextToken()); //에지
        int k = Integer.parseInt(st.nextToken());

        //인접 리스트
        ArrayList<Node>[] grape = new ArrayList[n + 1];

        for (int i = 0; i <= n; i++) {
            grape[i] = new ArrayList<>();
        }

        for (int i = 1; i <= m; i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            int c = Integer.parseInt(st.nextToken());
            grape[a].add(new Node(b,c));
        }

        //최단거리 배열 -> 우선순위 큐 배열로 변경 (k번째를 구해야 함)
        PriorityQueue<Integer>[] distQue = new PriorityQueue[n + 1];
        //두 정수를 비교하여, 더 큰 정수가 우선순위가 높도록 설정
        Comparator<Integer> comparator = new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1 < o2 ? 1 : -1;
            }
        };
        for (int i = 0; i <= n; i++) {
            distQue[i] = new PriorityQueue<>(k, comparator);
        }

        PriorityQueue<Node> queue = new PriorityQueue<>();
        //작은 값이 맨 위로 올라가, 꺼낼 때 작은 값부터 꺼내게 됨 (Node에서 compareTo 메서드 오버라이딩)
        queue.add(new Node(1, 0));
        distQue[1].add(0);
        while (!queue.isEmpty()) {
            Node now = queue.poll();
            for (Node node : grape[now.toNode]) {
                // 연결 관계 탐색
                if (distQue[node.toNode].size() < k) {
                    // 저장된 경로가 k개보다 작으면 경로 저장
                    distQue[node.toNode].add(now.e + node.e);
                    queue.add(new Node(node.toNode, now.e + node.e));
                } else if (distQue[node.toNode].peek() > now.e + node.e) {
                    // 저장된 경로가 k개이고, 새로운 경로가 가장 큰 값보다 작으면 추가 (k개보다 많이 저장할 필요 X)
                    distQue[node.toNode].poll(); // K번째 가장 큰 값 꺼내서 삭제
                    distQue[node.toNode].add(now.e + node.e); // 새로운 경로 값 추가
                    queue.add(new Node(node.toNode, now.e + node.e));
                }
            }
        }

        StringBuilder sb = new StringBuilder();
        for (int i = 1; i <= n; i++) {
            if (distQue[i].size() == k) {
                sb.append(distQue[i].peek()).append("\n");
            } else sb.append(-1).append("\n"); //k번째 경로 존재하지 않으면 -1
        }
        System.out.println(sb);
    }

    static class Node implements Comparable<Node> {
        int toNode;
        int e;

        @Override
        public int compareTo(Node node) {
            return this.e - node.e;
        }

        public Node(int toNode, int e) {
            this.toNode = toNode;
            this.e = e;
        }
    }
}

출처

[백준 1854] K번째 최단경로 찾기 (JAVA)