[백준] 11724번 연결 요소의 개수 (JAVA)

문제사항

실버 2단계 문제였다.

방향이 없는 그래프 이므로 무방향 그래프 문제이다.

방향 그래프 / 무방향 그래프 / 가중치 방향 그래프가 나온다면 DFS 혹은 BFS 로 풀어야 한다.

세 개의 그래프에 대해 어떻게 접근해야 하는지 모르겠다면 이전 DFS, BFS 기초를 전체적으로 다룬 포스팅을 참고하길 바란다.

[백준] Recursive, Tree, Graph(DFS, BFS 기초)

알고리즘 분류

1. 완전 탐색
2. DFS
3. BFS

DFS로 풀었다.

코드

import java.io.*;
import java.util.*;

public class Main {

    static int n,m, components = 0;
    static boolean[][] graph;
    static boolean[] ch;

    static void DFS(int v) {
        ch[v] = true;
        for (int i = 1; i <= n; i++) {
            if (graph[v][i] && !ch[i]) {
            	//무방향에선 1행 1열, 2행 2열, 3행 3열 ,, 등은 무조건 flase
                DFS(i);
            }
        }
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());
        graph = new boolean[n + 1][n + 1];
        ch = new boolean[n + 1];
        for (int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            graph[a][b] = graph[b][a] = true;
        }

        for (int i = 1; i <= n; i++) {
            if (!ch[i]) {
                DFS(i);
                components++;
            }
        }
        System.out.println(components);
    }

}

제일 의아 했던거는 왜 ch[] 체크 배열을 해제하는 코드가 없을까? 였다.

그동안 방향 그래프만 다룬 코드만 접근했어서 처음엔 이유를 몰랐다.

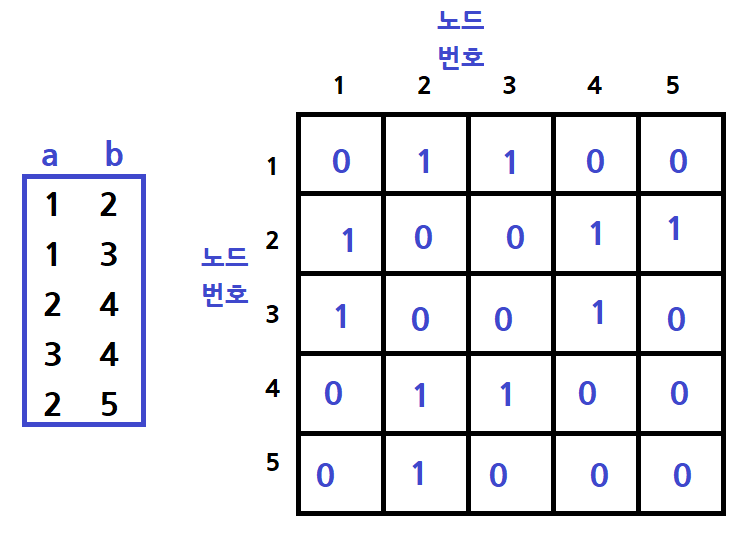
예시로 위와 같은 무방향 그래프가 있다고 가정하자

여기서 데칼코마니 마냥 반으로 가르면 동일하게 1(True)이 찍혀있다.

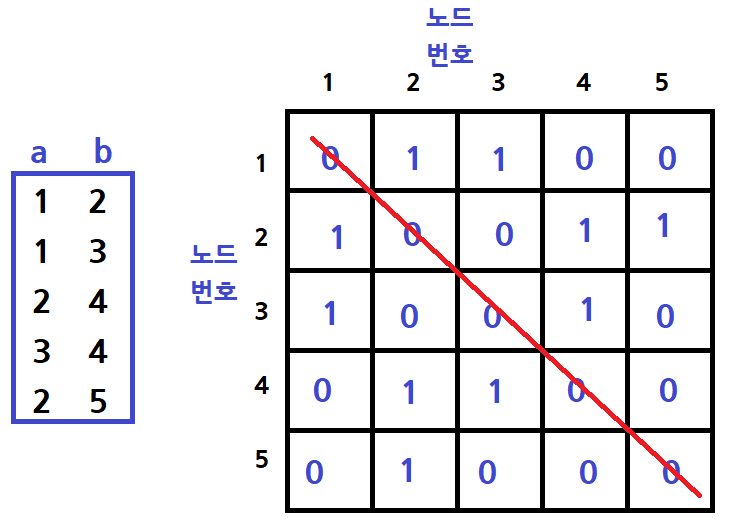
그렇다 왼쪽 위부터 오른쪽 아래로 떨어지는 대각선은 무조건 0(Flase)일 수밖에 없으므로

static void DFS(int v) {
  ch[v] = true;
  for (int i = 1; i <= n; i++) {
      if (graph[v][i] && !ch[i]) {
      //무방향에선 1행 1열, 2행 2열, 3행 3열 ,, 등은 무조건 flase
      DFS(i);
      }
  }
}

DFS 매개변수로 받는 숫자 값을 ch 배열의 true 값으로 두고, if문에서는 graph[][] 배열이 동일한 숫자가 행과 열에 위치하도록 코드를 구현한 것이다.