[백준] 1300번 K번째 수 (JAVA)

문제사항

골드 1단계 문제였다.

역시 아래와 같이 풀면

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        int k = Integer.parseInt(br.readLine());

        int[] B = new int[N * N];
        int idx = 0;
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                B[idx++] = i * j;
            }
        }

        Arrays.sort(B); // 배열 B를 오름차순으로 정렬

        System.out.println(B[k - 1]); // k번째 수 출력
    }
}

메모리 초과이고, 이중 for문 쓰지말고 이진 검색 (Binary Search) 알고리즘을 사용해야 한다.

---

문제가 말하고자 하는 것은 2차원 배열에 i * j에 해당하는 값을 모두 넣어주고, 이것을 1차원 배열로 오름차순 정렬을 요구하고 있다.

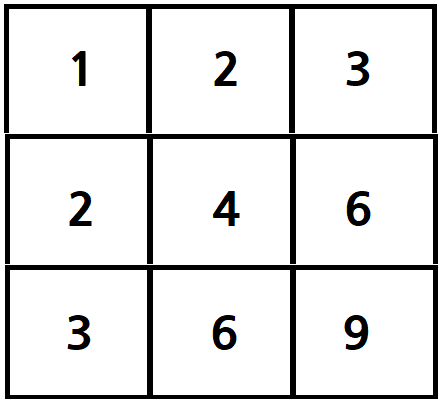
여기서 7번째 배열 값은 6이다.

알고리즘 분류

1. 이진 검색 (Binary Search)

Binary Search(이진검색 알고리즘) 개념 살펴보기

코드

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int k = Integer.parseInt(br.readLine());

        int lt = 1, rt = k, answer = 0;

        while (lt <= rt) {
            int mid = (lt + rt) / 2;
            int cnt=0;

            for (int i = 1; i <= n; i++) {
                cnt += Math.min(mid / i, n);
            }

            if (cnt < k) {
                lt = mid + 1;
            } else {
                answer = mid;
                rt = mid - 1;
            }
        }
        System.out.println(answer);
    }
}

여기서 이해하는데 시간이 걸렸던 부분은 이 부분이다.

for (int i = 1; i <= n; i++) {
	cnt += Math.min(mid / i, n);                
}

예제를 들어 설명하자면, N=3, k=7이라고 하였으니 7번째로 작은 수를 찾아야 한다.

A = 1 2 3
    2 4 6 
    3 6 9

이 배열의 값들을 오름차순으로 정렬하면 다음과 같다

A = [1, 2, 2, 3, 3, 4, 6, 6, 9]

앞서 말했듯이 여기서 7번째 수, 즉 k=7일 때의 수는 6이다.

우리는 이분 탐색을 사용하여 k번째 수가 무엇인지 찾는다.

1. 초기 left = 1, right = k = 7 이다.

2. mid = (left + right) / 2 = 4

3. 그리고 count += Math.min(mid / i, N)을 계산한다.

  1행: count += min(4/1, 3) = 3 // 1 2 3 중 1 2 3 모두
  2행: count += min(4/2, 3) = 2 // 2 4 6 중 2 4
  3행: count += min(4/3, 3) = 1 // 3 6 9 중 3
  
  총 count = 3 + 2 + 1 = 6

4. 6 < k(=7) 이므로, left = mid + 1 = 5로 갱신한다.

이런 식으로 이분 탐색을 계속하면서 count가 k와 같아지는 mid 값을 찾는다.

그 mid 값이 k번째 수가 된다.

Math.min(mid/i, N) 은 i행에서 mid 이하의 값들의 개수를 구해주는 식이다.

이를 모든 행에 대해 계산하여 누적하면 전체 mid 이하 값들의 개수를 알 수 있다.