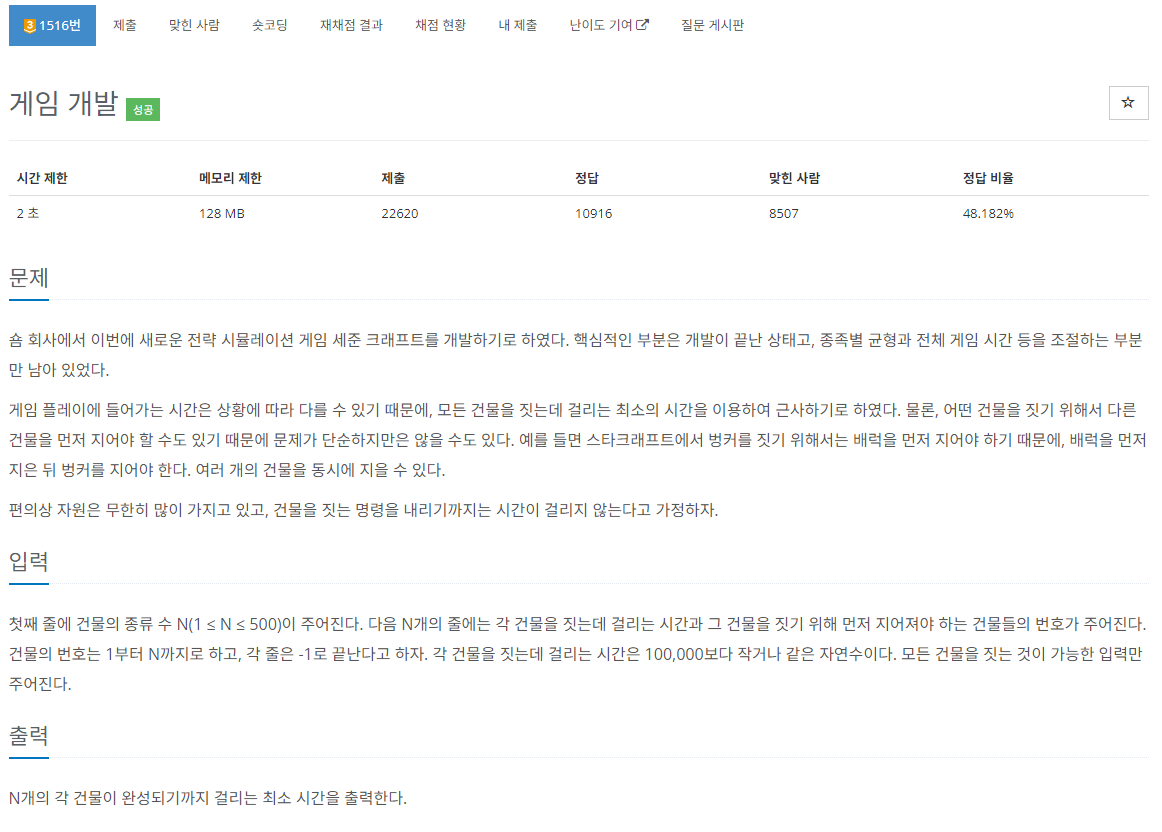
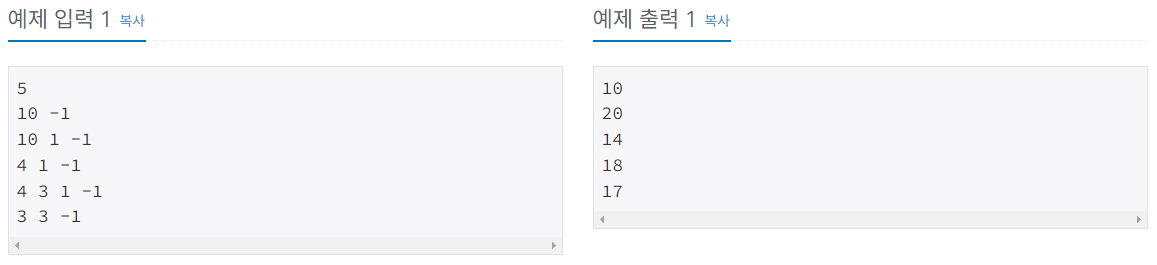
문제사항
골드 3단계 문제였다.
앞서 포스팅한 [백준] 2252번 줄 세우기 (JAVA) 문제도 위상 정렬 문제였는데, 해당 문제도 위상 정렬 알고리즘을 이용한 문제이다.
위상 정렬 알고리즘에 대해 궁금하다면 위 포스팅을 참고하자.
여기서 주의해야 하는 점이 있다.
건물을 짓는 과정은 순차적으로 이루어지기 때문에 위상정렬을 이용하여 해결할 수 있다.
중요한 점은 여러 개의 건물이 동시에 지어질 수 있다는 점이다.
예를 들어, C건물을 짓기위하여 A건물과 B건물이 필요하다고 가정해보자.
그리고 A건물이 지어지는 데 걸리는 시간은 10초, B건물이 지어지는데 20초가 걸린다면, C건물을 짓기 위한 최종 시간은 20초가 된다.
A, B를 동시에 건설하기때문에 더 긴 시간을 택해야하는 것이다.
코드에 대입해서 생각해보면 A가 1번째 건물, B가 2번째 건물, C가 3번째 건물이므로 indegree[3] = 2가 될 것이다.
그리고 indegree[1] = indegree[2] = 0이므로 큐에 A와 B 건물이 들어가게 된다.
큐에서 A를 빼 내고, indegree[3] = 1이된다.
동시에 result[3] = max(0, 0 + 10) = 10으로 초기화할 수 있다.
다시, 큐에서 B를 빼 내고, indegree[2] = 0이 된다.
동시에 result[3] = max(10, 0 + 20) = 20으로 초기화할 수 있다.
알고리즘 분류
- 그래프 (위상 정렬)
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st;
int n = Integer.parseInt(br.readLine());
//그래프 이차원 리스트
List<List<Integer>> list = new ArrayList<>();
for (int i = 0; i <= n; i++) {
list.add(new ArrayList<>());
}
//특정 건물을 지을 때, 먼저 지어져야 할 건물 개수 (=진입차수 저장 배열)
int[] indegree = new int[n + 1];
//특정 건물을 지을 때, 걸리는 시간
int[] time = new int[n + 1];
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
time[i] = Integer.parseInt(st.nextToken());
while (true) {
int num = Integer.parseInt(st.nextToken());
if (num == -1) {
break;
} else {
list.get(num).add(i);
indegree[i]++;
}
}
}
Queue<Integer> que = new LinkedList<>();
for (int i = 1; i <= n; i++) {
if (indegree[i] == 0) {
que.offer(i);
}
}
//각 건물이 완성되기까지 걸리는 최소 시간
int[] result = new int[n + 1];
while (!que.isEmpty()) {
int now = que.poll();
for (int i = 0; i < list.get(now).size(); i++) {
int next = list.get(now).get(i);
indegree[next]--;
// next 건물을 짓기 전까지 걸린 시간 계산
result[next] = Math.max(result[next], result[now] + time[now]);
if (indegree[next] == 0) {
que.offer(next);
}
}
}
//위에서 next 건물 짓기 전까지 걸린 시간을 계산하였으니, next 건물이 지어진 후 걸린 시간까지 계산하여 출력
for (int i = 1; i <= n; i++) {
sb.append(result[i] + time[i]).append("\n");
}
System.out.println(sb);
}
}

