문제사항
플래티넘 5단계 문제였다.
앞서 포스팅한 [백준] 2252번 줄 세우기 (JAVA), [백준] 1516번 게임 개발 (JAVA) 문제도 위상 정렬 문제였는데, 해당 문제도 위상 정렬 알고리즘을 이용한 문제이다.
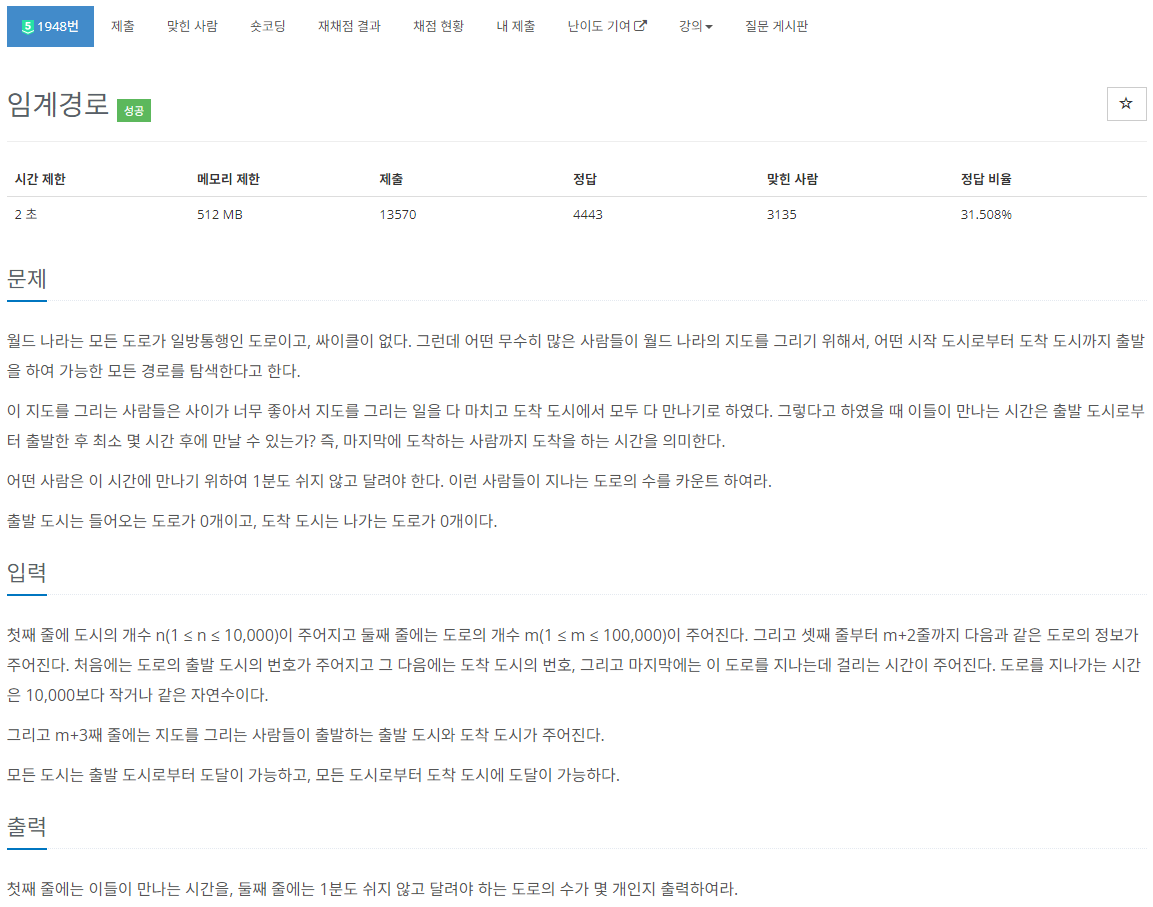
여기서 말하는 모든 사람이 만나는 시간은 최장시간이며 도착도시의 최대비용을 구하면 된다.
그리고 1분도 쉬지 않고 달려야하는 도로의 수는 최대값을 만드는 경로(=모든 사람이 만나는 시간)의 수와 같다.
출발하는 도시와 도착하는 도시가 지정되기 때문에 목적에 따라 큐에 넣는 노드를 다르게 해주어야 한다.
일반적인 위상정렬 문제라고 생각하면 안되는게, 1분도 쉬지 않고 달려야 하는 도로의 개수를 구하는 데에는 역방향 그래프에서 위상정렬을 수행해야 한다는 점이다.
따라서 정방향 그래프와 역방향 그래프를 만들어주었다. 정방향 그래프에서는 시작도시를 출발점으로 정하여 위상정렬을 수행한다. 여기서 임계경로(path[])는 각 노드에서 도착 도시까지의 도달하는데 걸리는 최대 시간을 말한다.
그러므로 모든 사람이 만나는 시간은 마지막 노드의 임계경로 값이다.
정방향 그래프에서 임계경로를 모두 설정해주면, 역방향 그래프에서도 위상정렬 수행이 가능하도록 구현하였다. 이때 역방향 그래프에서 정방향에서 수행했던 도착도시가 시작점이 된다.
여기서 한 정점까지 소모한 비용 + 도착 도시까지의 최대 비용(=임계경로)를 더해주는 경우를 cnt로 카운팅해주었다.
추가로 역방향 그래프에서 방문한 노드는 다시 방문할 수 없도록, 방문 배열을 선언하여 구분해주는 작업은 필수로 들어가야 한다. (중복 카운팅됨)
path[도착도시]와 cnt를 출력하면 된다.
알고리즘 분류
- 그래프 (위상 정렬)
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int m = Integer.parseInt(br.readLine());
ArrayList<ArrayList<Node>> graph = new ArrayList<>(); // 정방향 그래프
ArrayList<ArrayList<Node>> reverse_graph = new ArrayList<>(); // 역방향 그래프
for (int i = 0; i <= n; i++) { //크기 +1만큼은 더 크게 해줘야함 (i<=n)
graph.add(new ArrayList<Node>());
reverse_graph.add(new ArrayList<Node>());
}
// 진입차수 저장 배열
int[] indegree = new int[n + 1];
// 각 출발 도시(시작노드)부터 도착 도시(마지막노드)까지 임계경로(최대시간)
int[] path = new int[n + 1];
StringTokenizer st;
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
//정방향: a->b, a에서 b까지의 가중치 = e
graph.get(a).add(new Node(b, e));
//다음 노드를 진입차수 대상으로 두고 +1
indegree[b]++;
//역방향: b->a, b에서 a까지의 가중치 = e
reverse_graph.get(b).add(new Node(a, e));
}
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
//위상정렬
Queue<Integer> que = new LinkedList<>();
que.offer(start);
while (!que.isEmpty()) {
int now = que.poll();
for (Node node : graph.get(now)) {
//다음 노드를 진입차수 대상으로 두고 -1
indegree[node.toNode]--;
//동일 노드에 간선이 둘 이상이면(=진입차수가 0보다 큰 경우) Math.max 작용 (큰값 대입)
path[node.toNode] = Math.max(path[node.toNode], path[now] + node.e);
//진입차수가 0이면 que에 추가
if (indegree[node.toNode] == 0) {
que.offer(node.toNode);
}
}
}
// 역위상정렬
que.offer(end);
int cnt = 0;
boolean[] visited = new boolean[n + 1];
visited[end] = true;
while (!que.isEmpty()) {
int now = que.poll();
for (Node node : reverse_graph.get(now)) {
//도달 정점에서의 최대 비용 + 간선에서 소모한 비용 = 최대 비용(고정 값일 것)
if (path[now] == path[node.toNode] + node.e) {
cnt++;
if (!visited[node.toNode]) {
que.offer(node.toNode);
visited[node.toNode] = true;
}
}
}
}
StringBuilder sb = new StringBuilder();
sb.append(path[end]).append("\n");
sb.append(cnt);
System.out.println(sb);
}
static class Node {
int toNode; // 다음 노드
int e; // 현재 노드와 다음 노드 간의 간선의 가중치
public Node(int toNode, int e) {
this.toNode = toNode;
this.e = e;
}
}
}

