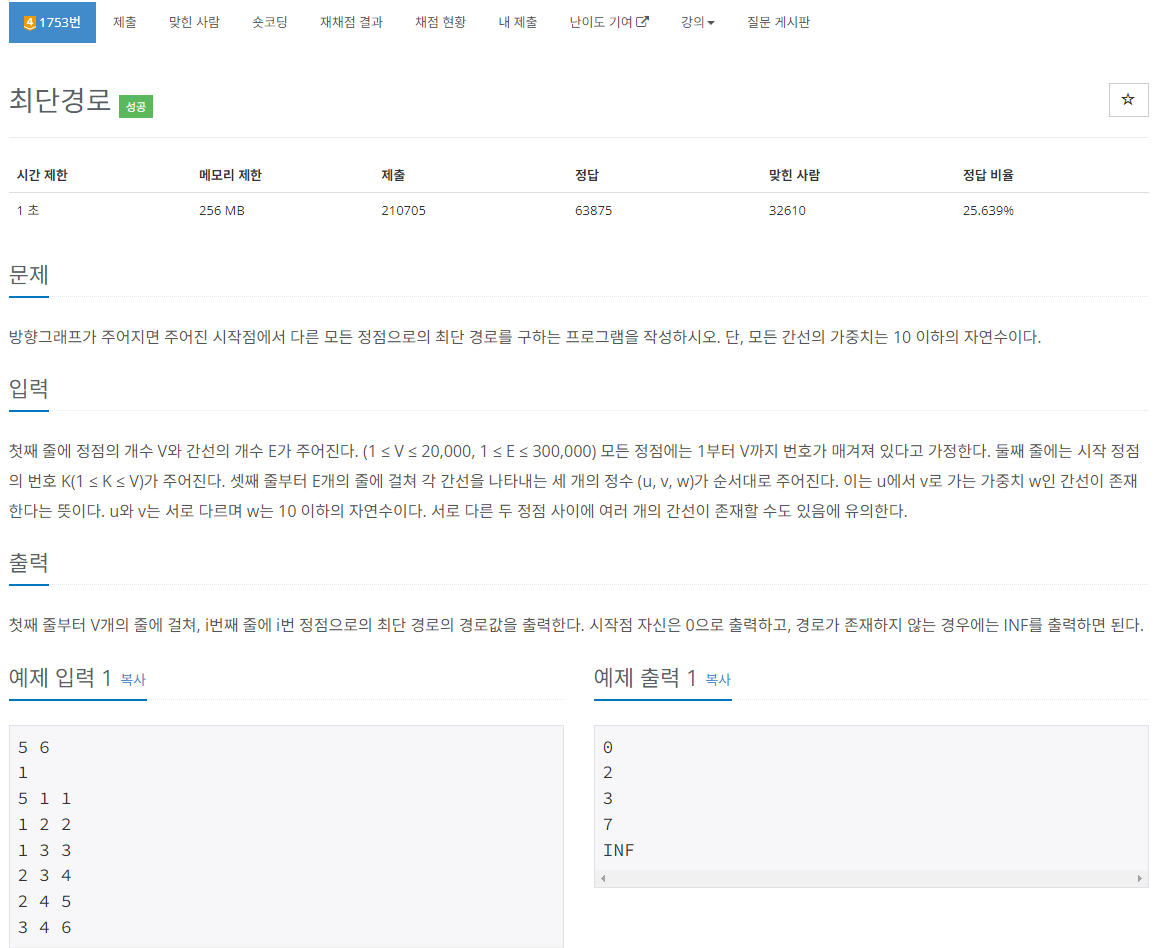
문제사항

백준 4단계 문제였다.

다익스트라 알고리즘의 대표적인 문제로, 이론부터 알아보자.

'다익스트라' 란?

다익스트라 알고리즘은 최단거리 알고리즘 이다.

특징은 시작점이 주어진다는 점, 음수 간선이 주어지지 않는다는 점이다.
(시작점 O, 음수 간선 X)

과정을 살펴보자.

1. 인접 리스트로 그래프 구현하기

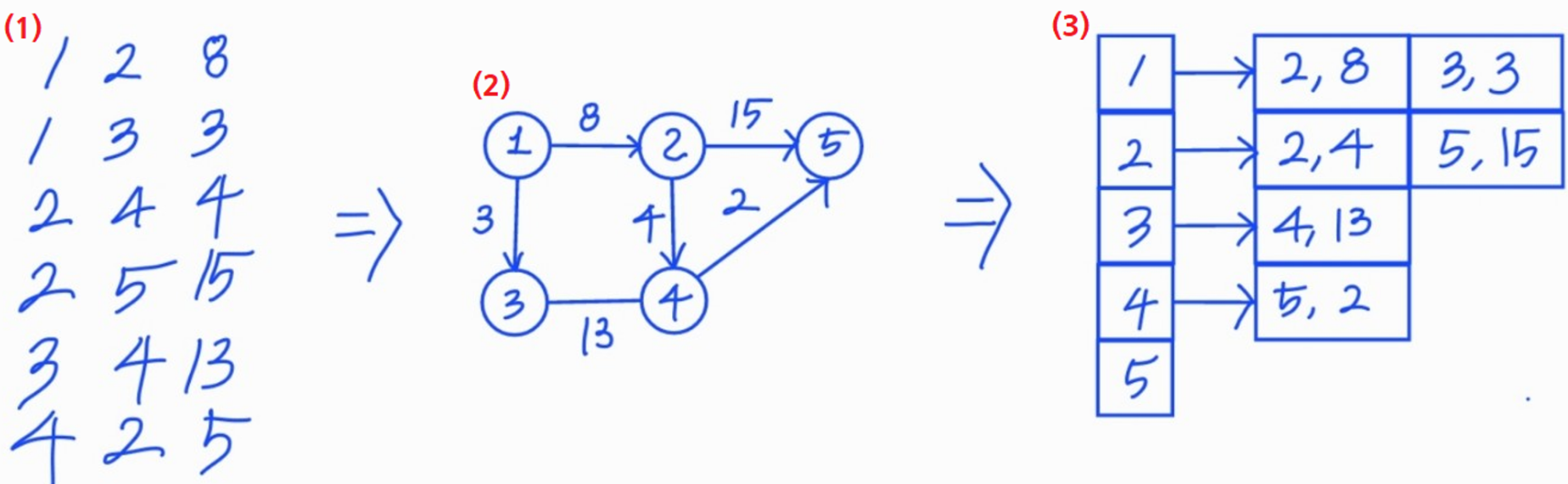
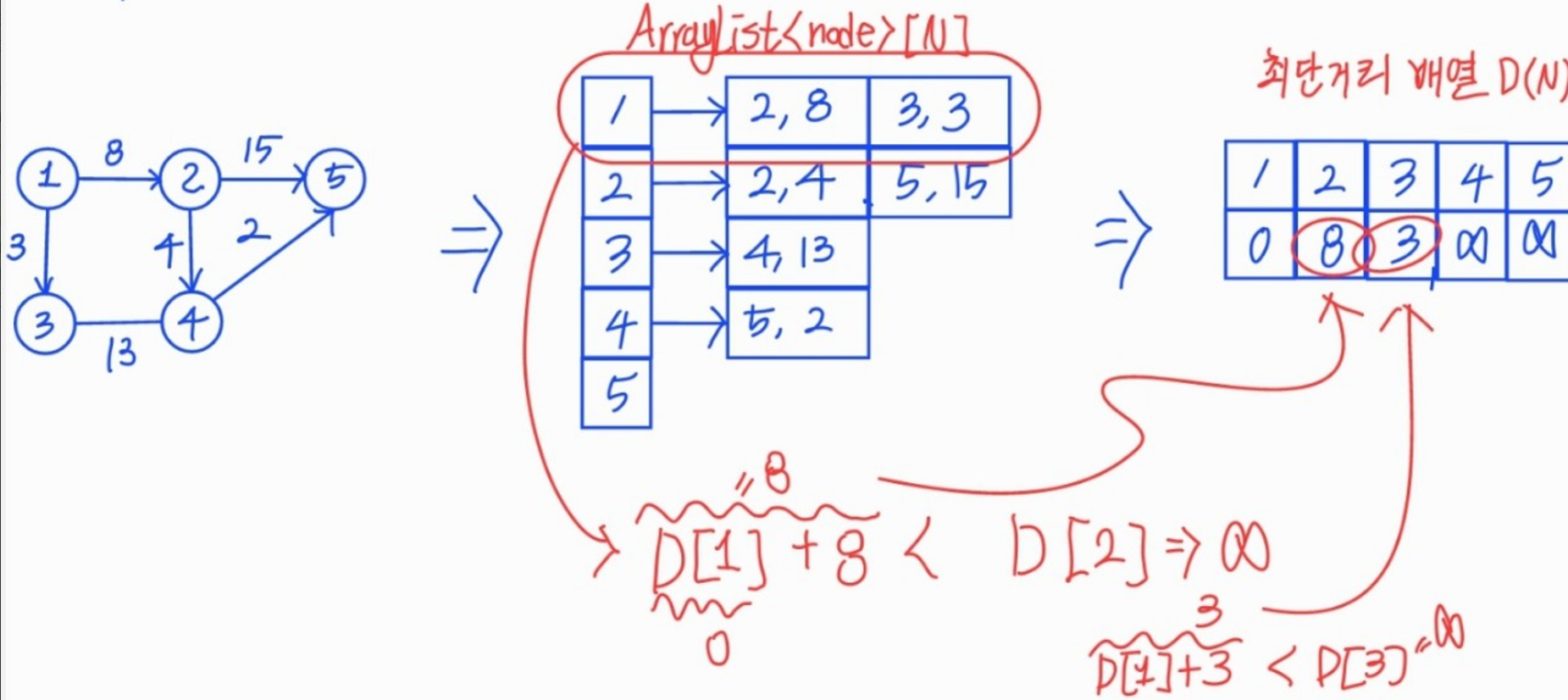
• (1)번과 같이 1에서 2로 가는 가중치가 8인 엣지(e), 2에서 5로 가는 가중치가 15인 엣지(e) 등 입력 값이 주어지면 (2)번과 같은 그래프로 표현할 줄 알아야 한다.

• (2)번과 같은 그래프로 표현이 된다면 (3)번과 같이 데이터를 자료구조로 담아 표현할 줄 알아야 한다.

인접 행렬로 구현해도 좋지만 시간 복잡도 측면 N의 크기가 큰 것을 대비해 인접 리스트를 선택해 구현하는 것이 좋다.

2. 최단 거리 배열 초기화하기

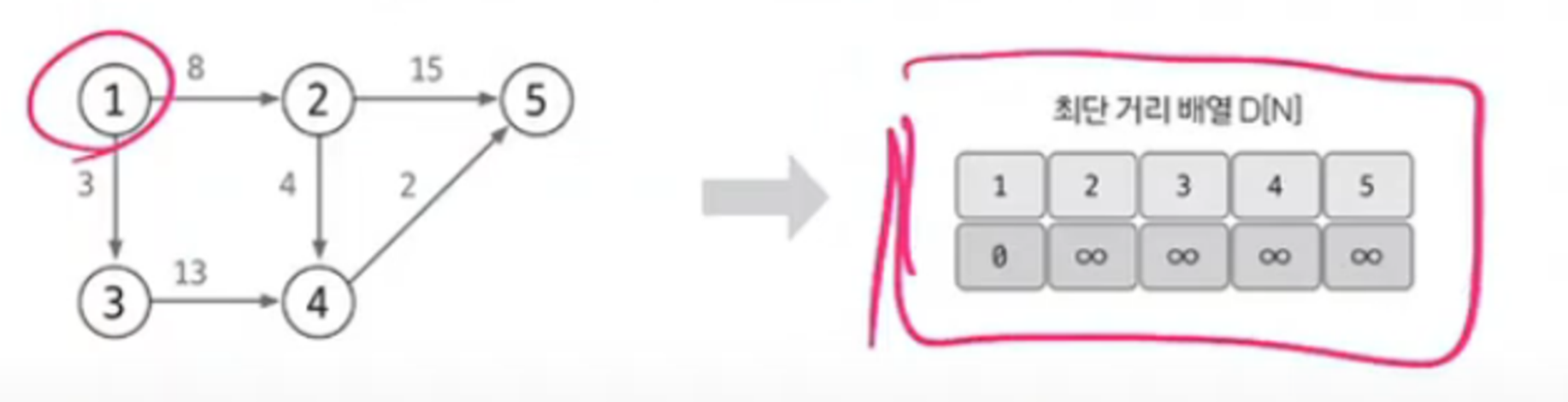
• 최단 거리 배열을 만들고, 출발 노드 0 이외 노드 무한으로 초기화한다.

3. 값이 가장 작은 노드 고르기

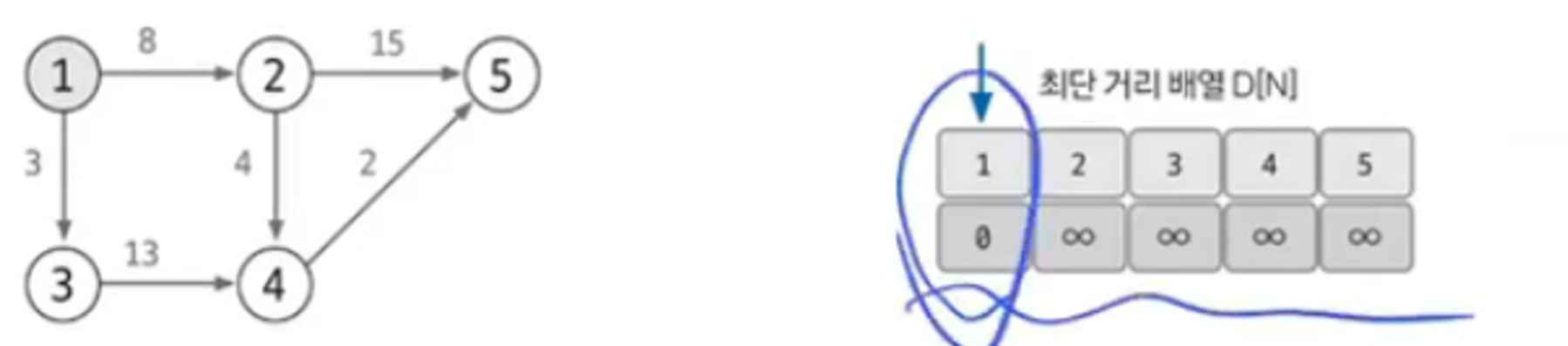
• 최단 거리 배열에서 현재 값이 가장 작은 노드를 고른다.

• 여기선 값이 0인 출발 노드에서 시작한다.

4. 최단 거리 배열 업데이트하기

• 그래프 구현 시 저장해 놓은 연결 리스트 이용해서 선택된 노드에서 에지 값을 바탕으로 다른 노드 값을 업데이트한다.

• 연결 노드의 최단 거리는 두 값 중 더 작은 값으로 업데이트한다.
  ( 자료구조는 Queue보다는 PriorityQueue로 구현을 선호, compareTo로 Node 간 거리 비교도 필수이다.)

5. 과정 3~4 반복해 최단 거리 배열 완성하기

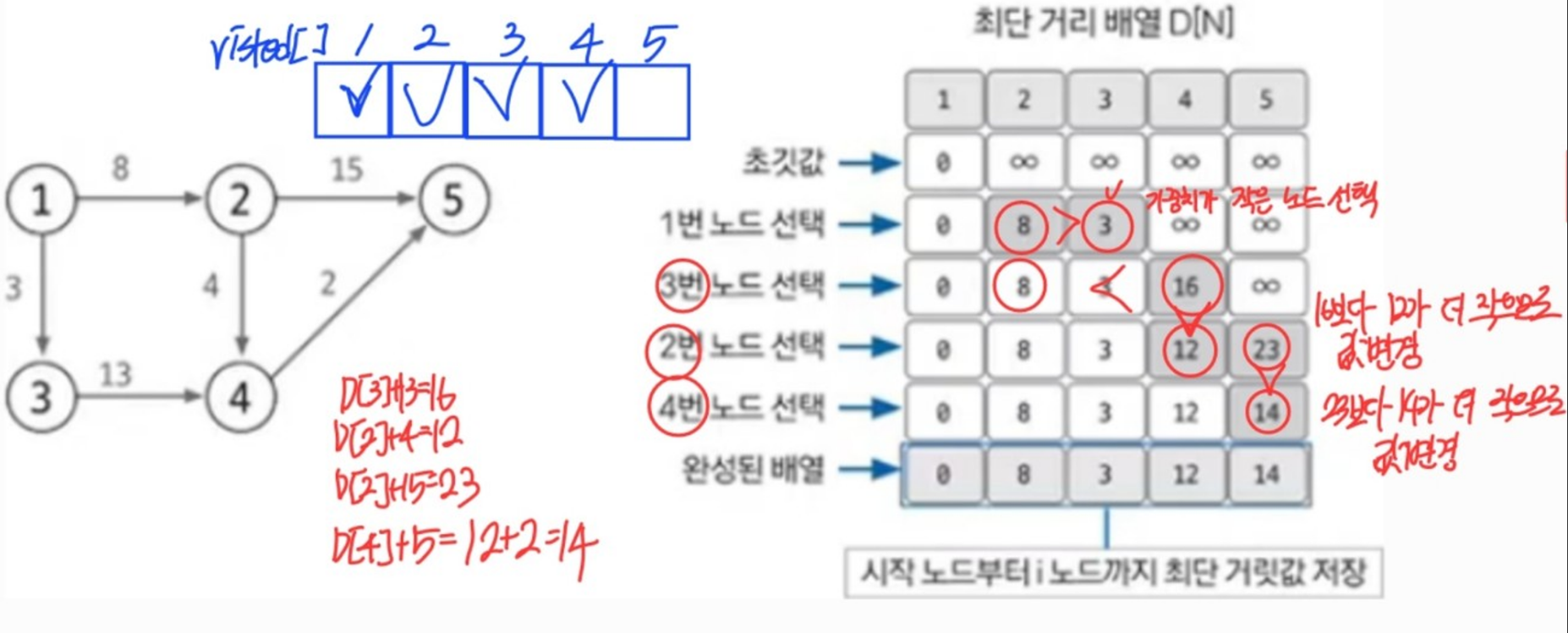
• 모든 노드가 처리될 때까지 과정 3~4를 반복한다.

• 과정 4에서 선택 노드가 될 때마다 다시 선택되지 않도록 방문 배열을 만들어 처리하고, 모든 노드가 선택될 때 까지 반복하면 최단거리 배열이 완성된다.

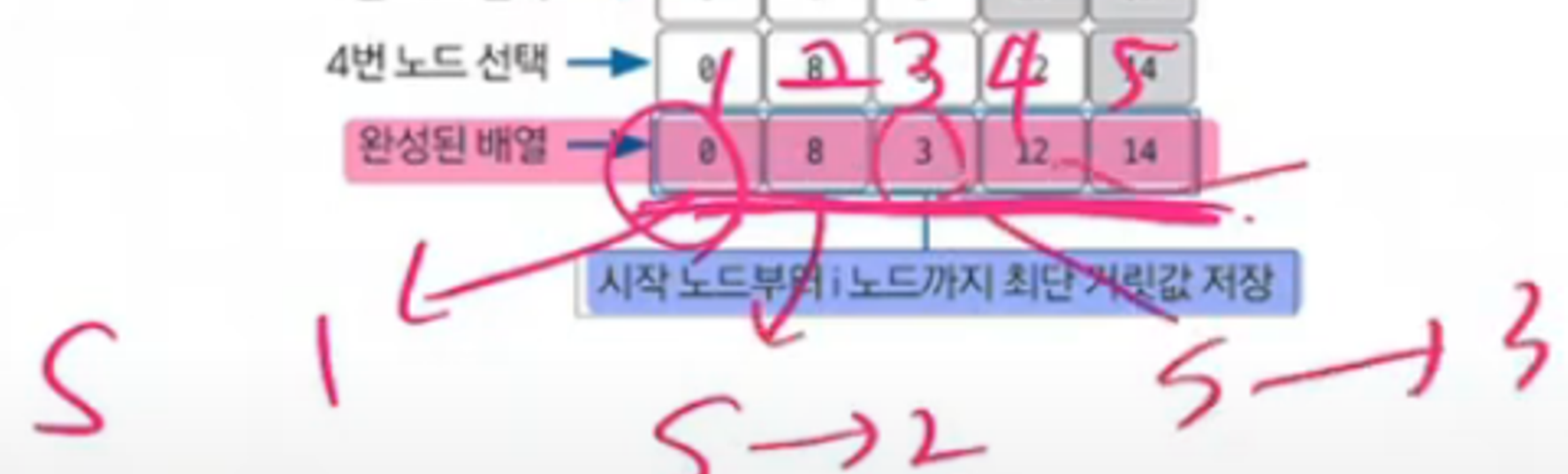
• 완성된 배열에서 각 인덱스의 값의 뜻은 다음과 같다

  시작 노드에서 1번 노드까지 가는데 걸리는 최단 거리
  시작 노드에서 2번 노드까지 가는데 걸리는 최단 거리
  시작 노드에서 3번 노드까지 가는데 걸리는 최단 거리
  시작 노드에서 4번 노드까지 가는데 걸리는 최단 거리
  시작 노드에서 5번 노드까지 가는데 걸리는 최단 거리

알고리즘 분류

1. 그래프 (다익스트라)

코드

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int V = Integer.parseInt(st.nextToken());
        int E = Integer.parseInt(st.nextToken());
        int K = Integer.parseInt(br.readLine());

        //인접리스트
        ArrayList<Node>[] grape = new ArrayList[V+1];
        //최단거리배열
        int[] D = new int[V + 1];
        //방문배열
        boolean[] visited = new boolean[V + 1];

        for (int i = 0; i <= V; i++) {
        	//인접리스트 배열 초기화
            grape[i] = new ArrayList<>();
            //인덱스 값 무한대로 초기화
            D[i] = Integer.MAX_VALUE;
        }

        for (int i = 1; i <= E; i++) {
            st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());
            grape[u].add(new Node(v, w));
        }

        //다익스트라 -> 우선순위 큐
        PriorityQueue<Node> que = new PriorityQueue<>();
        //시작 정점(출발 노드)의 인덱스 값은 0
        D[K] = 0;
        que.offer(new Node(K, 0));

        while (!que.isEmpty()) {
            Node now = que.poll();
            visited[now.toNode] = true;
            for (Node node : grape[now.toNode]) {
                if (!visited[node.toNode]) {
                    if (D[now.toNode] + node.e < D[node.toNode]) {
                        D[node.toNode] = D[now.toNode] + node.e;
                        que.offer(new Node(node.toNode, D[node.toNode]));
                    }
                }
            }
         }

        StringBuilder sb = new StringBuilder();
        for (int i = 1; i <= V; i++) {
            if (D[i] == Integer.MAX_VALUE) {
                sb.append("INF").append("\n");
            } else {
                sb.append(D[i]).append("\n");
            }
        }
        System.out.println(sb);
    }

    static class Node implements Comparable<Node>{
        int toNode;
        int e;

        @Override
        public int compareTo(Node o){
            return this.e - o.e;
        }

        public Node(int toNode, int e) {
            this.toNode = toNode;
            this.e = e;
        }
    }
}