Section 3. Two pointers, Sliding window[효율성: O(n^2)→O(n)]
00. 개념정리
Linear Search (선형검색 알고리즘)

10개 숫자가 있는 배열이 있다
그리고 그 배열에서 7이라는 숫자를 찾는다면
그렇다면 1번 아이템부터 차례로 7이 맞는지 확인할 것이다.
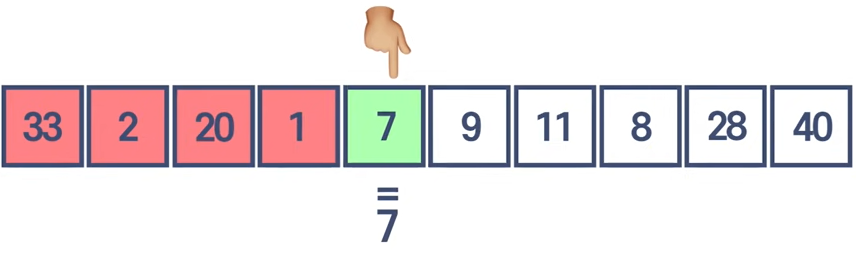
그렇게 순서대로 목표값을 찾는걸 뜻한다.
하지만 "선형검색"에서 최악의 경우는 찾는 배열이 맨 마지막에 있거나
혹은 배열에 아예 없는 경우이다.
이말인 즉슨, 배열이 커지면 커질수록 선형검색을 하는 시간 또한 길어진다.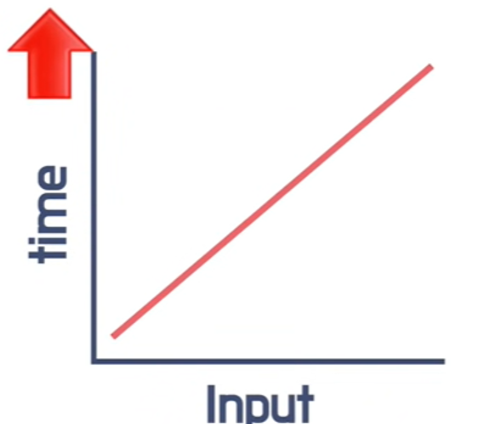
Input이 많으면 많을수록 수행하는 시간(Time) 역시 선형적으로 증가한다는 소리이다.Binary Search(이진검색 알고리즘)
선형검색보다 더 효율적이나, 이진검색 알고리즘은 모든 배열에 쓸 수는 없다.
"정렬된 배열(Sorted Array)"에서만 사용 가능하다.
Sorted Array란 배열들이 순서대로 정렬된 경우를 뜻한다.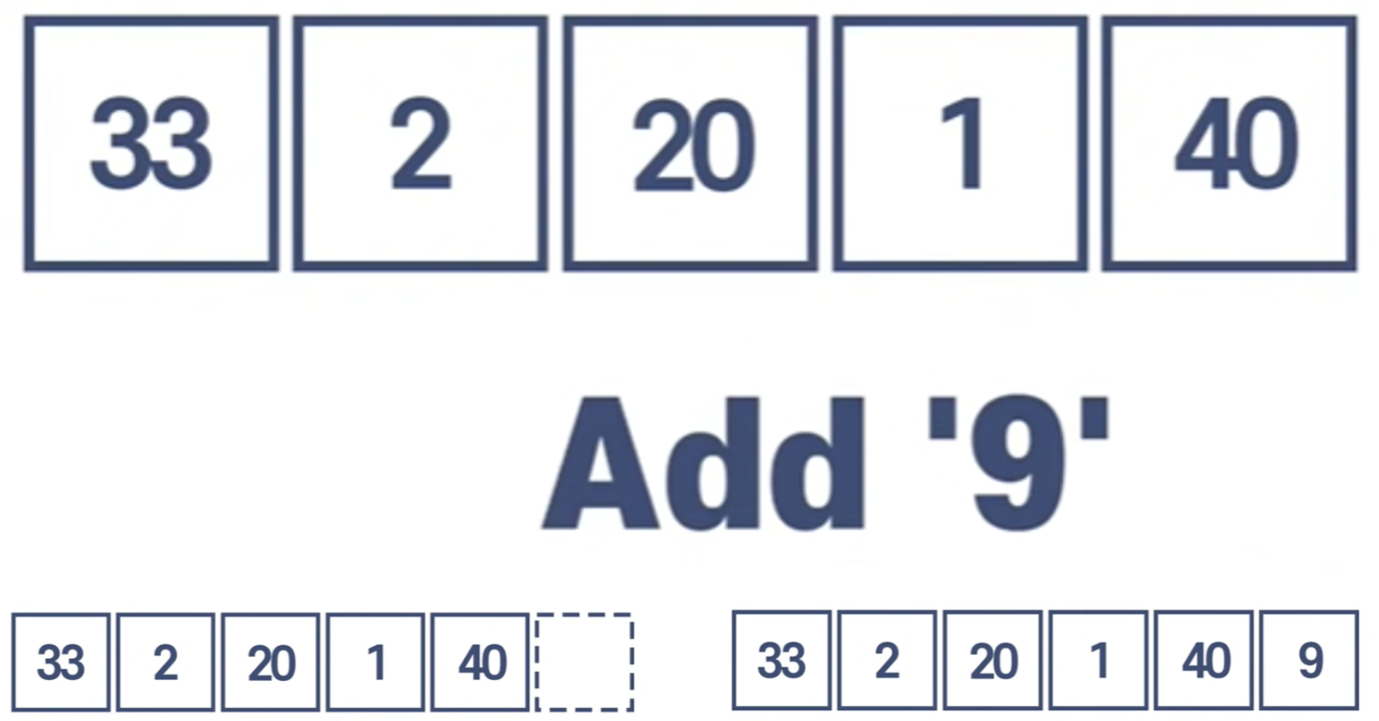
정렬이 안된 배열에 그냥 아이템을 추가하는 것은 맨 끝에 추가하면 된다.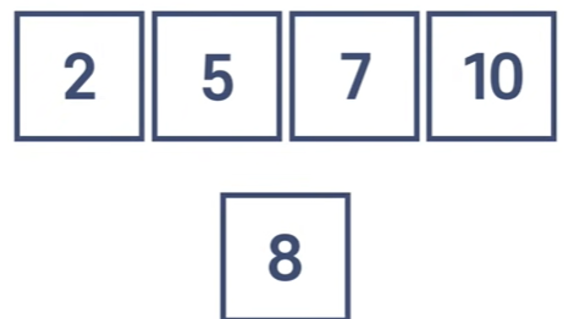
정렬된 배열에 아이템을 추가하는 것은 더 오랜 시간이 걸린다.
여기서 8이라는 아이템을 추가하고 싶다면
해당 배열에서 8보다 큰 아이템을 찾아야한다.
해당 아이템을 찾은 후, 8을 왼쪽에 추가해야 한다.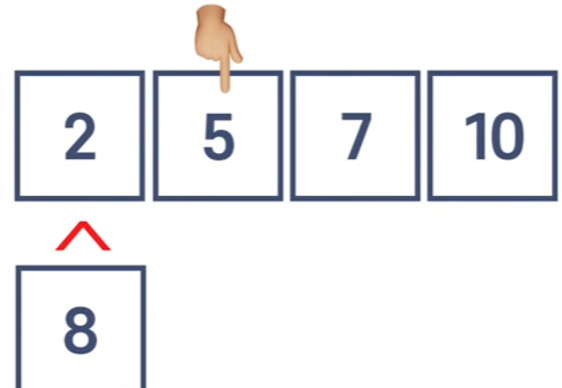
인덱스 0의 숫자인 2보다 8이 크므로 그 다음 인덱스로 넘어간다.
이 작업을 반복한다.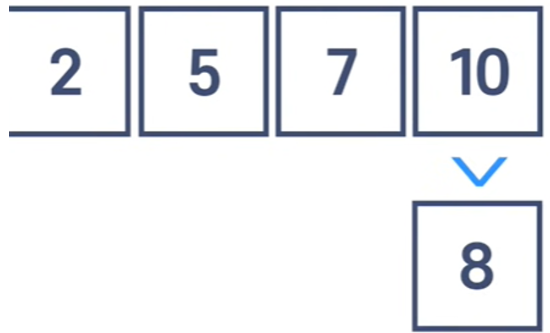
10은 8보다 크므로 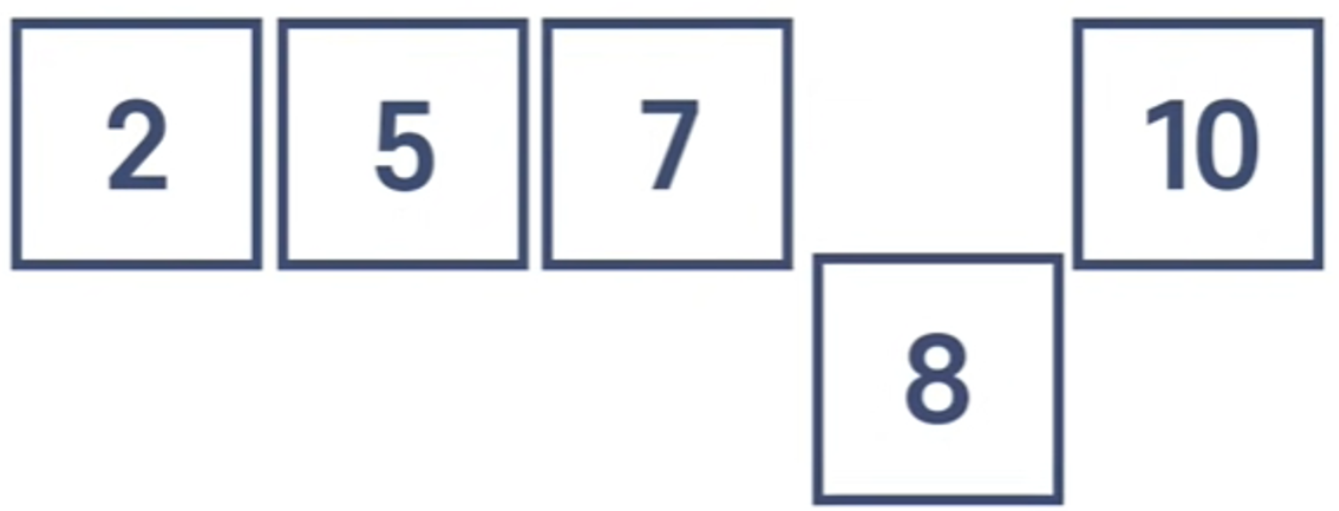
8을 추가하고 싶은 포지션의 오른쪽에 있는 아이템을 움직인 후 8을 위치한다.
그냥 정렬 안된 배열에 추가하는 것보다 정렬된 배열에 추가하는 것이 더 오랜 시간이 걸린다.
정렬된 배열에 '이진검색'을 해보도록 하자
'이진검색'은 하나를 두개로 쪼개는 것을 뜻한다.
선형 검색과 달리 이진 검색에서는 인덱스 0번부터 처음부터 검색을 하지 않는다.
이진 검색에서는 중간에서 시작한다.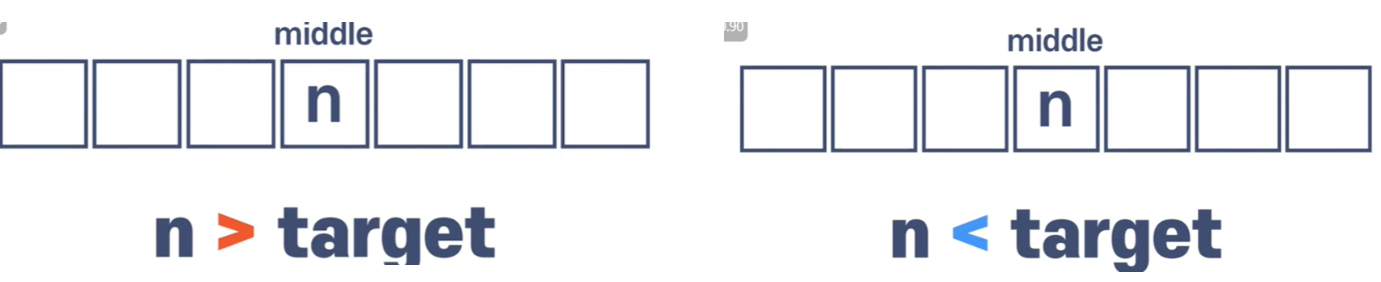
정 가운데에 있는 숫자가 우리 목표 숫자보다 큰지, 작은지를 확인한다.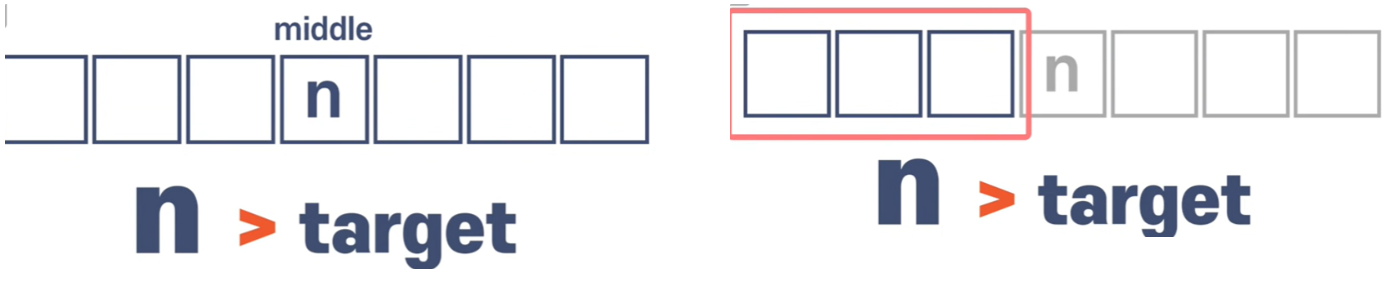
만약 아이템이 목표 숫자보다 크다면 목표 숫자가 아이템의 왼쪽으로 가게 된다. 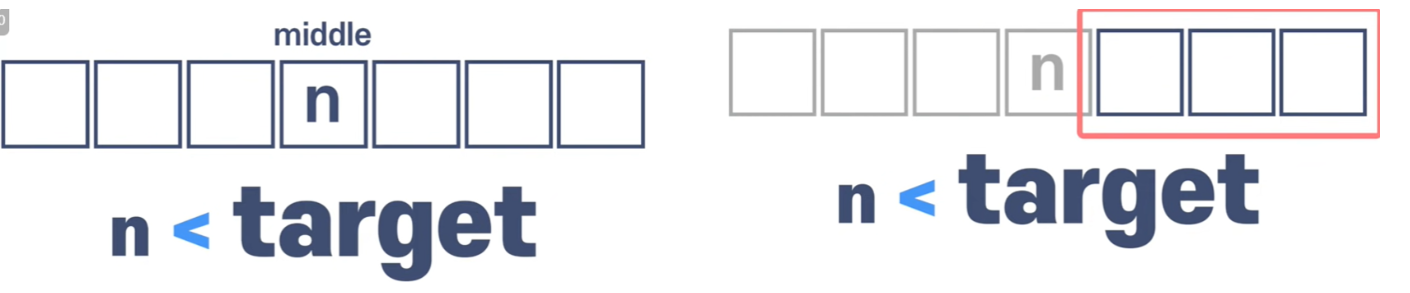
반대로 아이템이 목표숫자보다 작다면 목표 숫자가 아이템의 오른쪽으로 간다.
1에서 10까지 정렬된 상황에서 중간에서 시작하면 숫자는 5이다.
우리의 목표는 9이다. 따라서 5는 9보다 작으니까 아이템이 오른쪽으로 이동한다.
왼쪽은 싸그리 무시하게 된다.
해당 배열의 중간으로 이동한다. 이 경우엔 숫자가 8이 된다.
8은 9보다 작으므로 해당 아이템의 왼쪽은 무시하게 된다.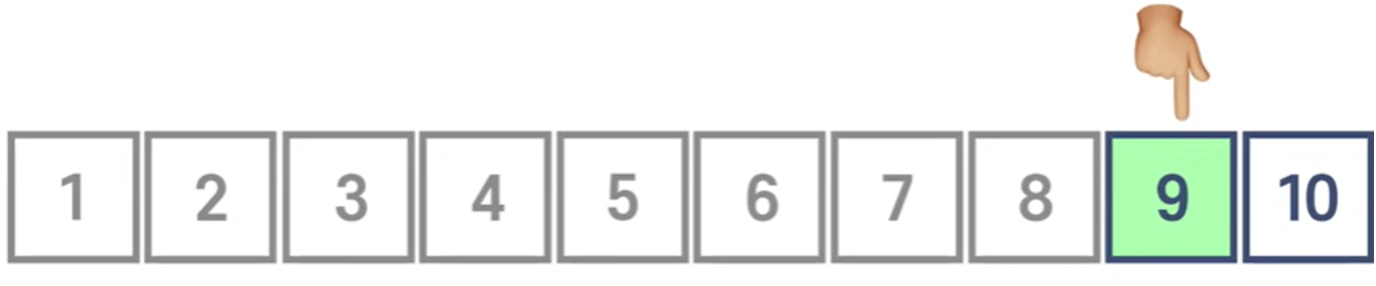
다음 프로세스에서 목표값을 찾게 된다.
이렇게 하면 3번만에 찾을 수 있다.
"선형검색"으로 하면 9번의 시도가 필요하지만 "이진검색"으로 3번으로 줄였다.
이진검색으로 아이템수를 두 배 늘린다고 검색 횟수가 두 배 늘어나는 것이 아니라 +1회 증가한다.
엄청 효율적이라 할 수 있다.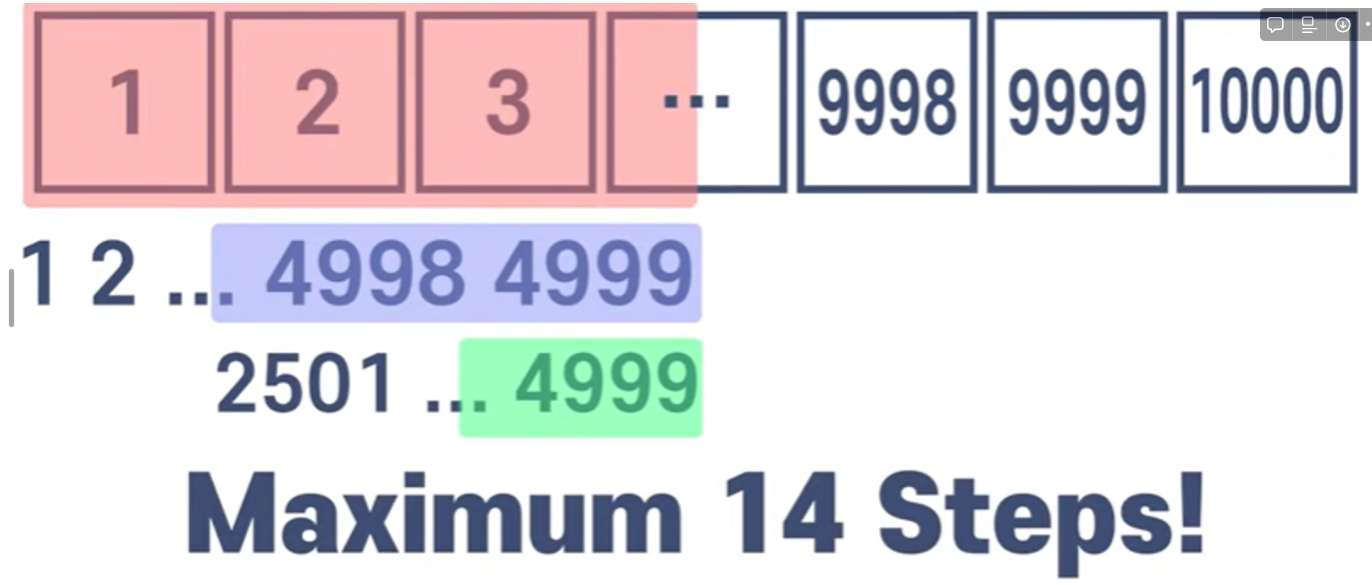
특히 큰 사이즈의 데이터를 처리할 때 효율적이다!
1만개의 아이템이 있는 "선형 검색"은 최악의 경우 1만개의 스텝을 요구한다.
반대로 "이진검색"으로 처리하면 최악의 경우에도 14개의 스텝만 소요된다.Big O
Big O를 사용하면, 시간복잡도를 빠르게 설명할 수 있다.
Big O를 이해하면 알고리즘 분석을 빠르게 할 수 있고, 언제 무엇을 쓸지 빠르게 파악이 가능하다.Case 1 → O(1)
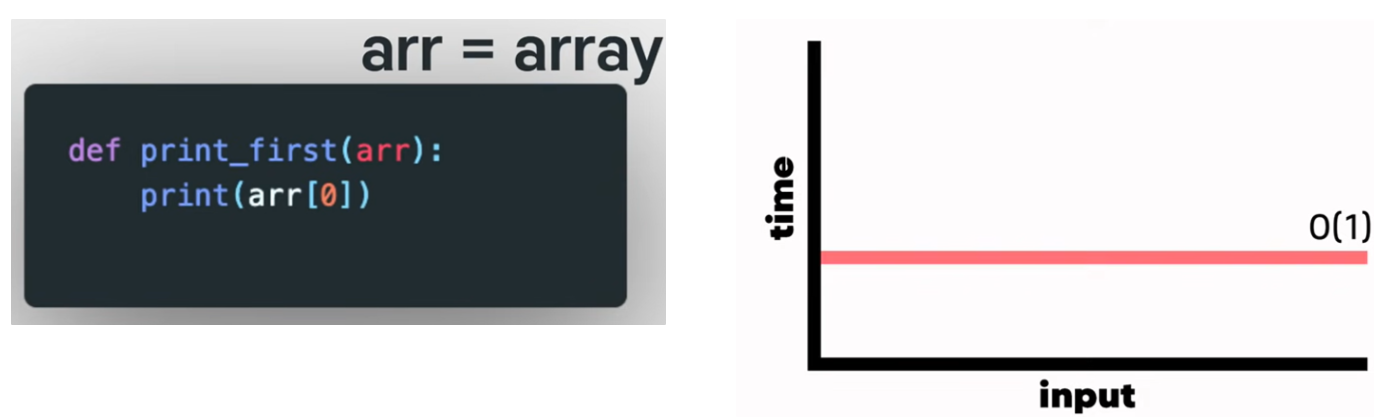
여기 배열을 인풋으로 사용할 함수가 있다.
이건 배열의 첫번째 element를 프린트할 것이다.
인풋 사이즈가 10이라면 이 함수는 딱 1번이면 실행이 끝난다.
인풋이 100개라도 끝나는건 1번이면 충분하다.
이 함수는 동일한 수의 스텝이 필요할 것이다.
이 함수의 시간복잡도는 상수 시간(Constant Time) 이라고 할 수 있다.
Big O에서는 이걸 위 표처럼 표현한다. 이것을 읽는 방법은 "O(1)"이다.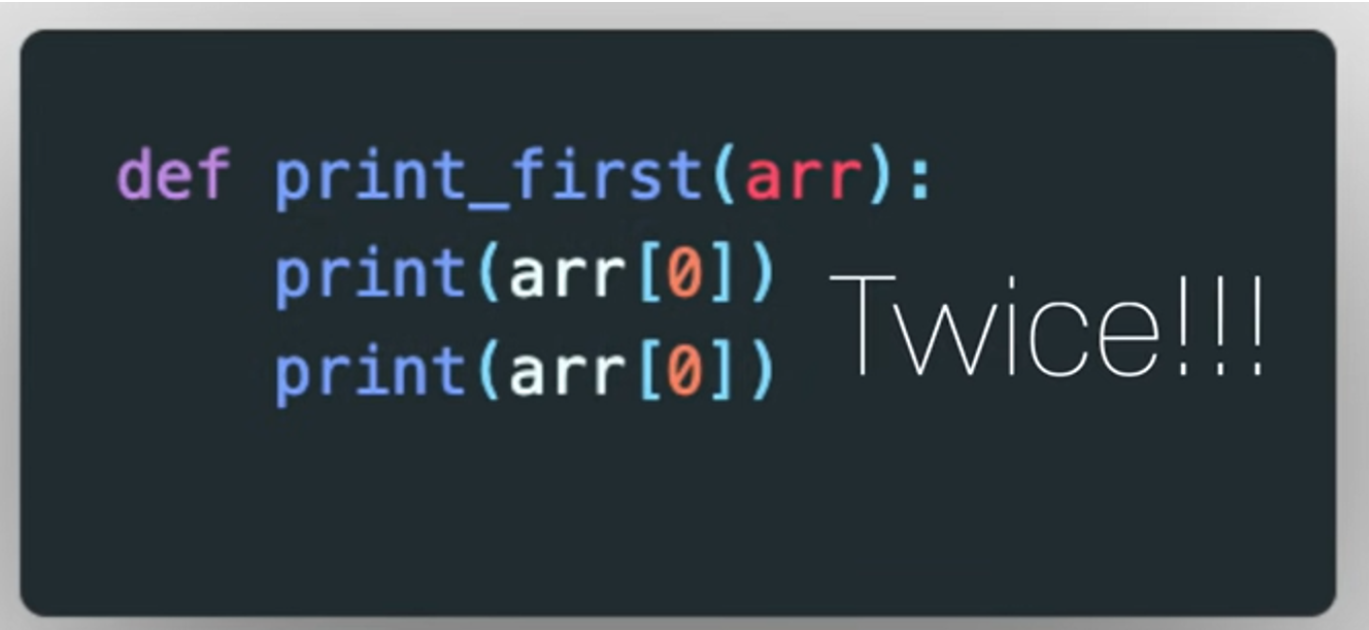
함수를 살짝 고쳐서 첫번째 아이템을 2번 프린트 해보자
2개의 스텝이 필요하게된다. 그러면 시간복잡도는 O(2)가 될까?
아니다. 여전히 O(1)이다.
Big O는 함수의 디테일에 대해선 관심이 없다. 큰 원리에만 관심이 있다.
Big O는 인풋 사이즈에 따라 어떻게 이 함수가 작동하는지 결정한다.
따라서 이 함수가 프린트를 2번 한다고 해도 O(1)로 표현하게 된다.
"BIG O는 상수(constant)에 신경 쓰지 않는다."Case 2 → O(N)
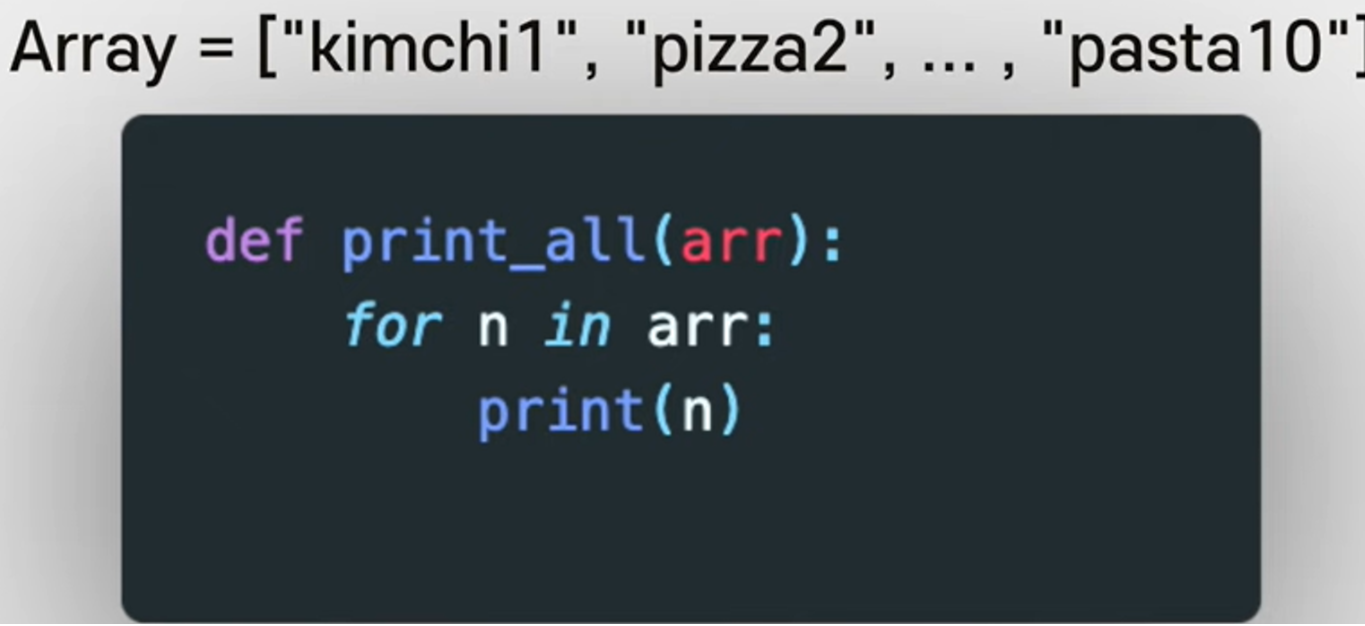
아이템을 전부 프린트 하는 함수가 있다.
배열 사이즈가 10이라면 10번 프린트한다.
마찬가지로 사이즈가 100이면 100번 프린트한다.
이는 선형검색과 비슷하다. 배열이 각각 아이템을 위해 모두 작업해야 한다.
배열이 커지면 필요 스텝도 커진다.
이를 BIG O로 나타내면 O(N)이라고 한다.
이전 예시에서 봤듯이 상수는 관계없이!
무슨 말이냐면, 함수를 반복하게 되면 이론적으로는 각 N마다 2번을 작업을 해서 O(N)이 되어야 하지만
하지만 2는 상수이기 때문에 버려지고 여전히 O(N)으로 표현한다
O(2N)이든 O(N)이든 전달하고자 하는 핵심 메시지는 동일하다.
"인풋이 증가하면 스텝이 증가한다."
따라서 O(N) 혹은 선형 시간복잡도를 그래프로 표현하면 대각선으로 보인다.Case 3 → O(N^2)
또 다른 시간복잡도로 2차 시간(Quadratic Time)이 있다.
2차 시간은 중첩반복(Nested Loops)이 있을 때 발생한다.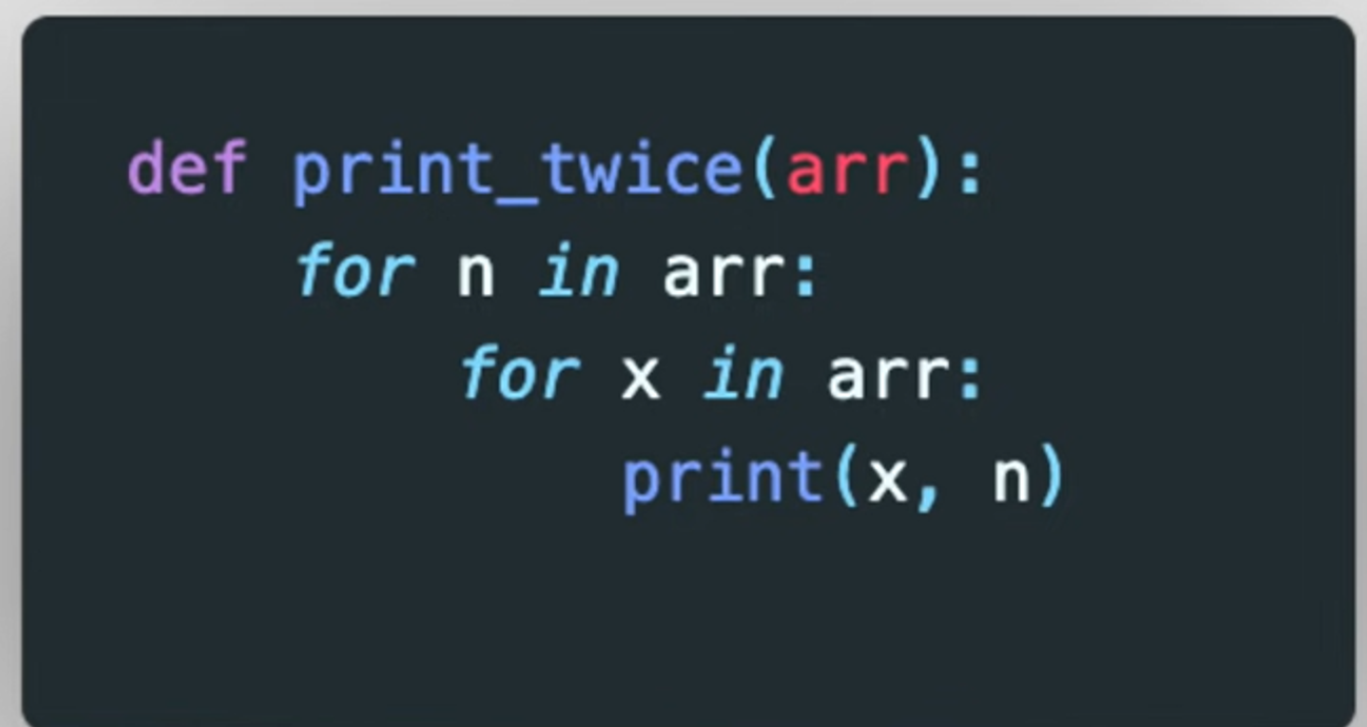
예를 들면, 이 함수의 경우 배열의 각 아이템에 대해 루프를 반복하며 실행한다.
따라서 시간복잡도는 인풋의 n^2인 것이다.
인풋이 10개라면 완성하는데 100번의 스텝이 필요한 것이다.
왜냐면 루프 안의 루프에서 함수를 실행하기 때문이다.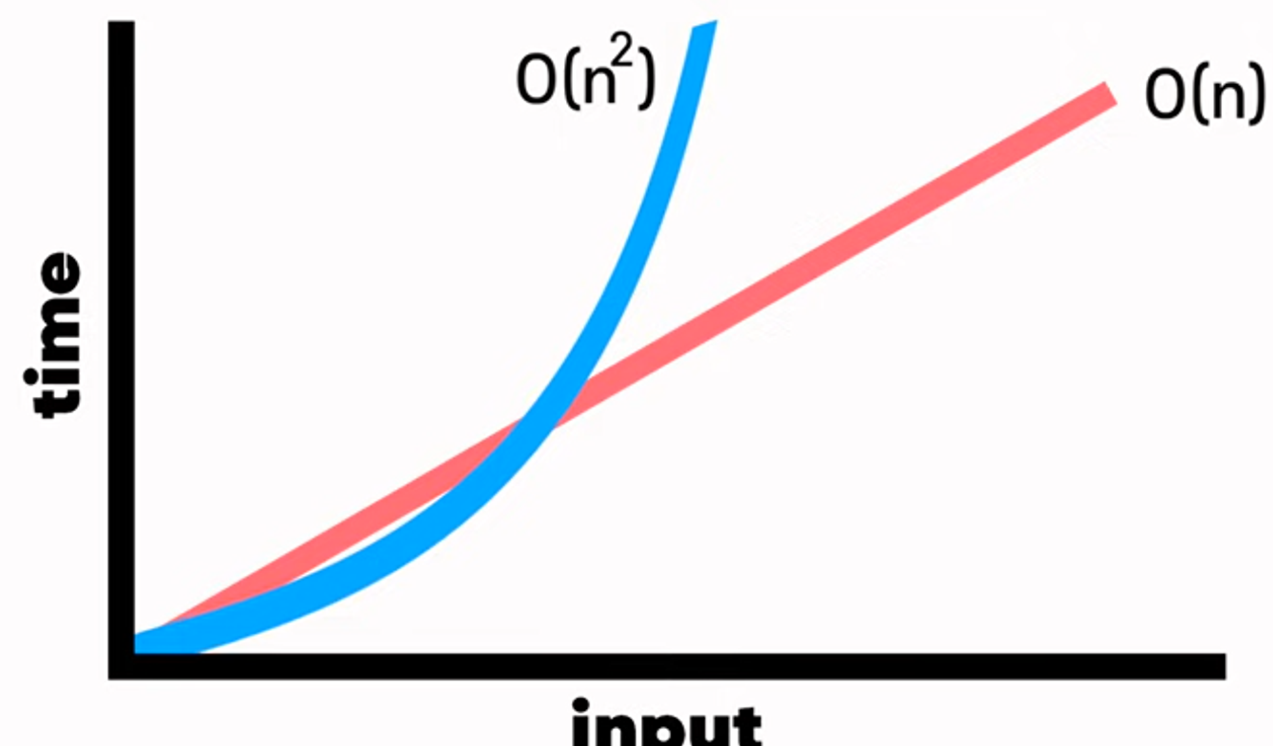
따라서 2차 시간(=O(n^2))이랑 비교하면 선형 시간 복잡도(=O(n))가 더 효율적인 것으로 선호된다.Case 4 → O(log n)
또 다른 시간복잡도로 로그 시간(Logarithmic Time) 이 있다.
이건 "이진검색 알고리즘" 설명에서 쓰인다.
로그에 대해 추가설명을 하자면 다음과 같다.
로그(logarithm)는 지수(exponent)의 정 반대이다.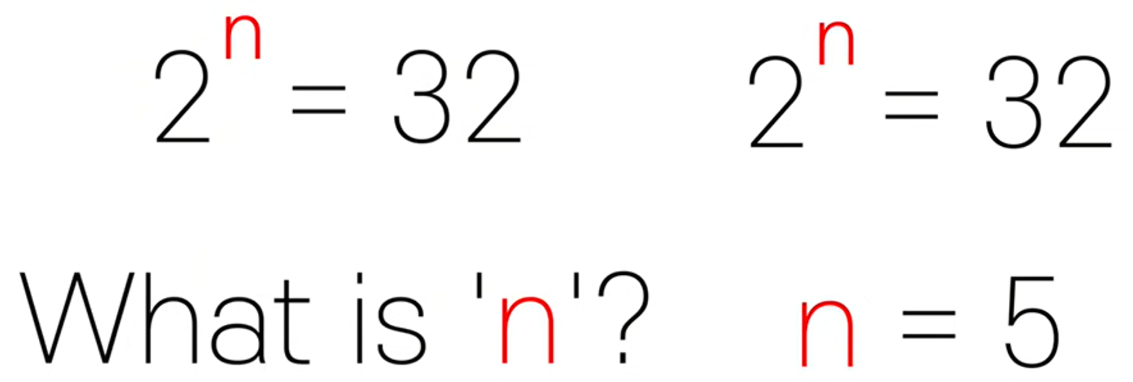
2는 몇 제곱해야 32이 되는걸까?
우리가 찾는 수는 5이다.
2^5=32 가 된다.
로그는 이 지수와 정 반대이다.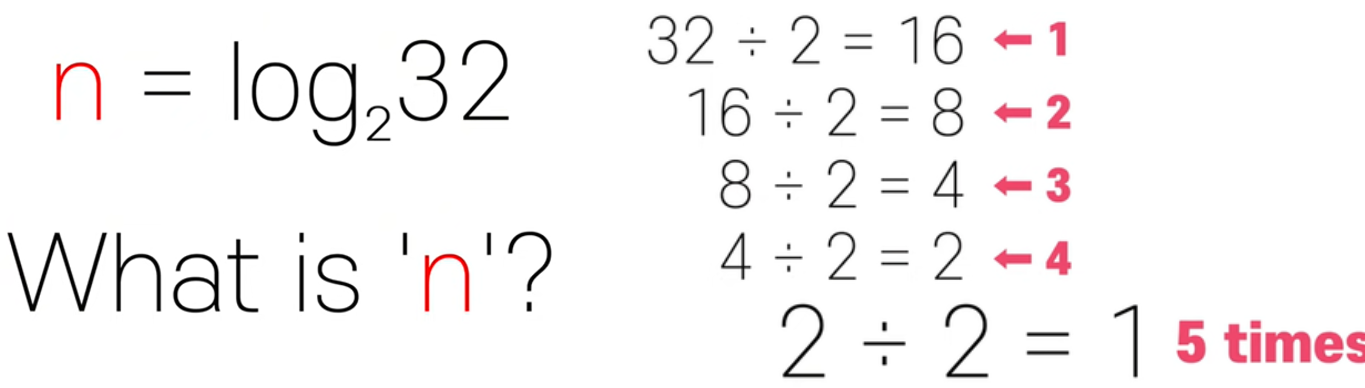
우리가 찾는 것은 몇 번을 나눠야 하는지 이다.
32를 2로 몇번을 나눠야 1이 나올까?
5번을 나눠야 1이 나오게 된다.
32의 밑이 2인 로그는 5라는 것을 알 수 있다.
이를 보니 '이진 검색'이 생각난다.
'이진 검색'은 인풋을 일단 반으로 나누고 시작한다. 매번 스텝을 진행할 때 말이다.
따라서 "이진검색"의 시간복잡도는 O(log n)이다.
설명했다시피, 32의 밑이 2의 로그는 5인데 이 경우 Big O 특성상 밑 숫자는 사라진다.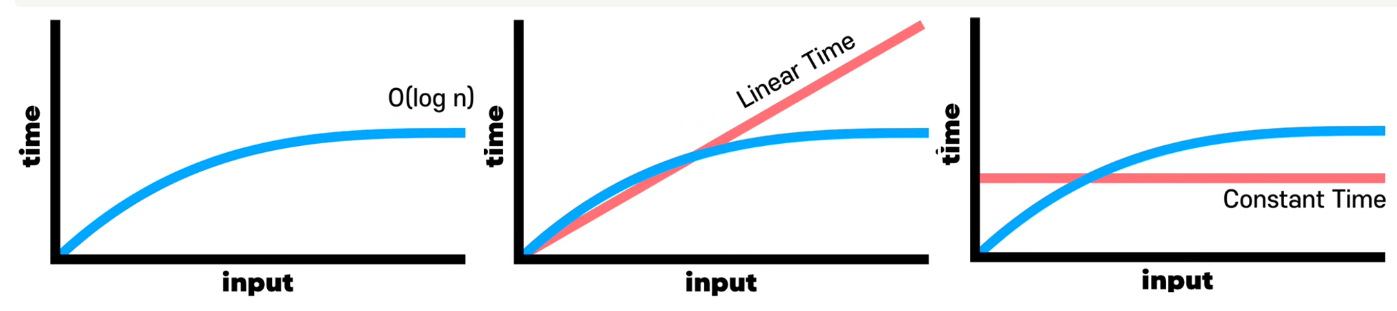
O(log n) 그래프의 모습은 다음과 같다.
선형 시간보다는 빠르고, 상수 시간보다는 느리다.
하지만 여기엔 트레이드 오프가 있다.
"이진검색은 정렬되지 않은 배열엔 사용할 수 없다." (정렬 필수)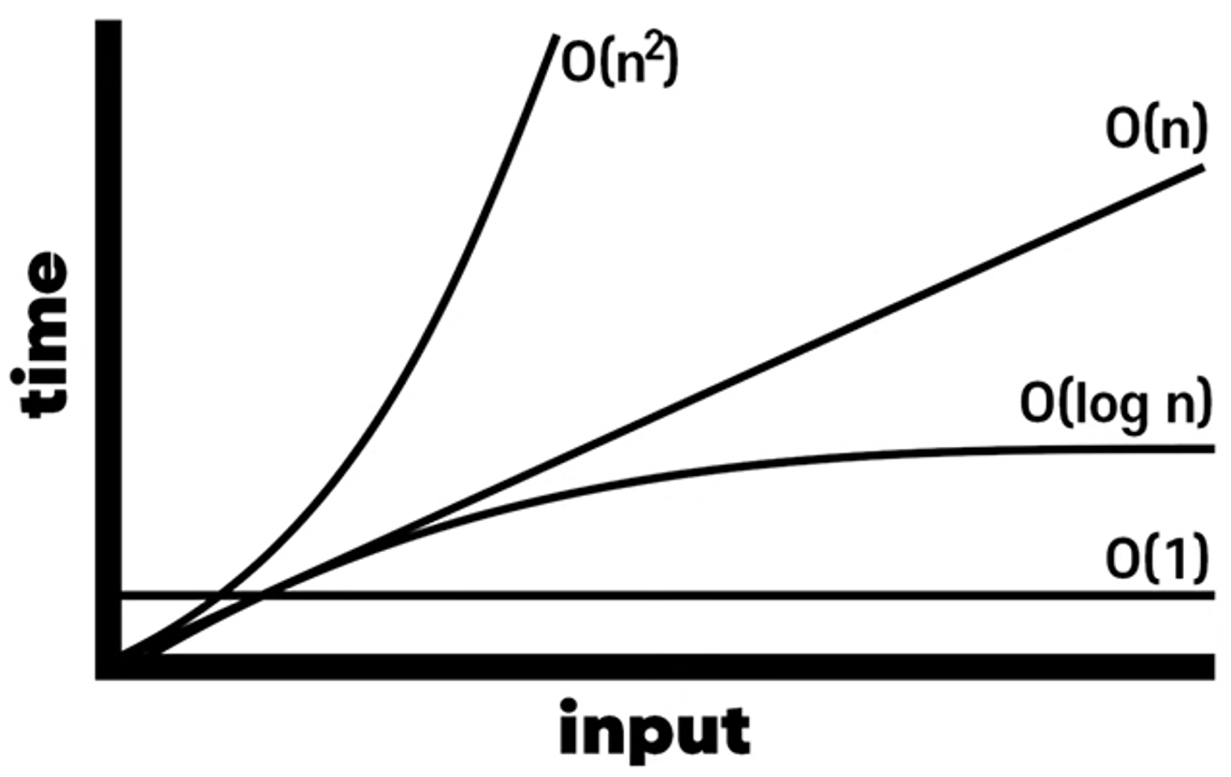
이 중 가장 선호되는건, 상수 시간(=O(1))이다.
인풋이 늘어도 변하지 않기 때문이다.
그 다음엔 로그 시간(=O(log n))이 좋고, 그 다음엔 선형 시간(=O(n))이 좋다.
그러나 지수 시간이나 이차 시간(=O(n^2))으로 가면 꽤 복잡해지게 된다.01. 두 배열 합치기
설명
오름차순으로 정렬이 된 두 배열이 주어지면 두 배열을 오름차순으로 합쳐 출력하는 프로그램을 작성하세요.입력
첫 번째 줄에 첫 번째 배열의 크기 N(1<=N<=100)이 주어집니다.
두 번째 줄에 N개의 배열 원소가 오름차순으로 주어집니다.
세 번째 줄에 두 번째 배열의 크기 M(1<=M<=100)이 주어집니다.
네 번째 줄에 M개의 배열 원소가 오름차순으로 주어집니다.
각 리스트의 원소는 int형 변수의 크기를 넘지 않습니다.출력
오름차순으로 정렬된 배열을 출력합니다.예시 입력 1
3
1 3 5
5
2 3 6 7 9예시 출력 1
1 2 3 3 5 6 7 9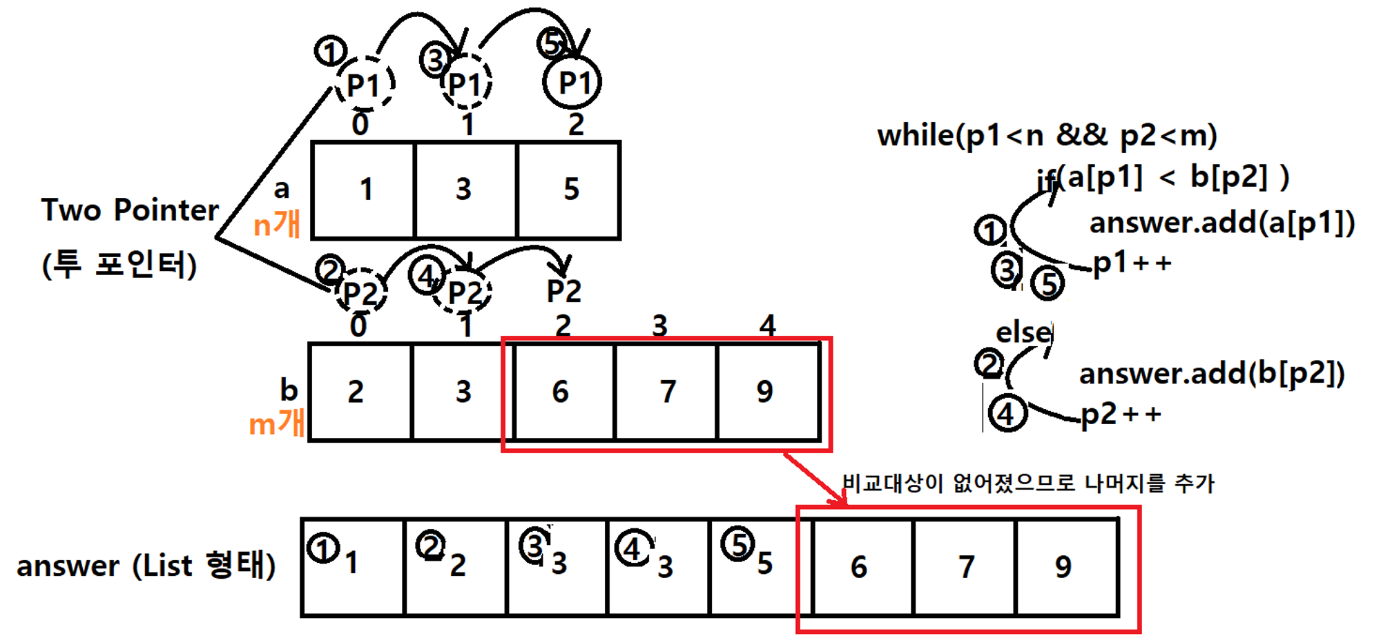
코드
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
// 두 배열 합치기
public class Main {
public List<Integer> solution(int n, int m, int[] a, int[] b) {
List<Integer> answer = new ArrayList<>();
int p1 = 0, p2 = 0;
//p1이 n과 동일한 숫자가 되거나, p2가 m과 동일한 숫자가 되면 while문 빠져나감
while (p1 < n && p2 < m) {
//후위연산자, add 한 후 p1값 1증가
if (a[p1] < b[p2]) answer.add(a[p1++]);
else answer.add(b[p2++]);
}
//p1이 아직 n보다 작은 상태
while(p1<n) answer.add(a[p1++]);
//p2가 아직 m보다 작은 상태
while(p2<m) answer.add(b[p2++]);
return answer;
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = kb.nextInt();
}
int m = kb.nextInt();
int[] b = new int[m];
for (int i = 0; i < m; i++) {
b[i] = kb.nextInt();
}
for (int x : T.solution(n, m, a, b)) System.out.print(x + " ");
}
}02. 공통원소 구하기
설명
A, B 두 개의 집합이 주어지면 두 집합의 공통 원소를 추출하여 오름차순으로 출력하는 프로그램을 작성하세요.입력
첫 번째 줄에 집합 A의 크기 N(1<=N<=30,000)이 주어집니다.
두 번째 줄에 N개의 원소가 주어집니다. 원소가 중복되어 주어지지 않습니다.
세 번째 줄에 집합 B의 크기 M(1<=M<=30,000)이 주어집니다.
네 번째 줄에 M개의 원소가 주어집니다. 원소가 중복되어 주어지지 않습니다.
각 집합의 원소는 1,000,000,000이하의 자연수입니다.출력
두 집합의 공통원소를 오름차순 정렬하여 출력합니다.예시 입력 1
5
1 3 9 5 2
5
3 2 5 7 8예시 입력 1
2 3 5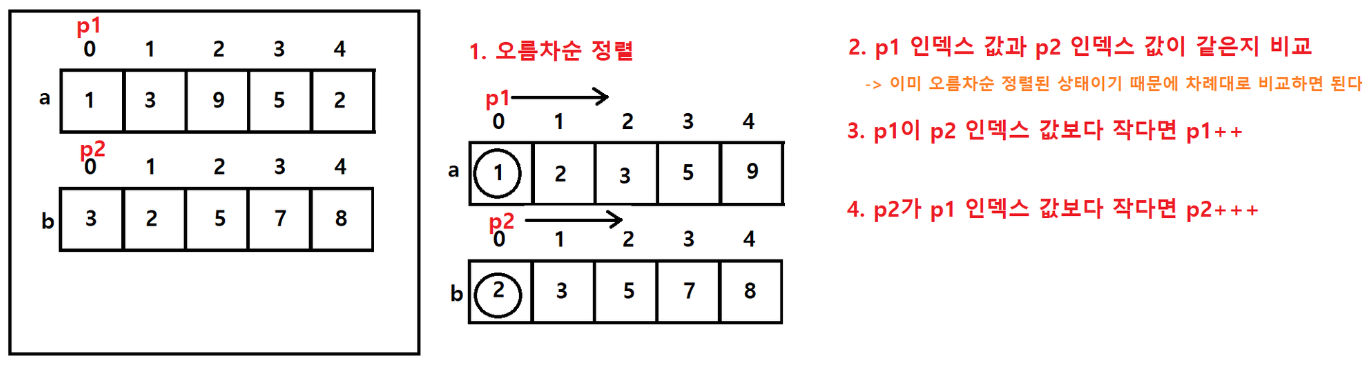
코드
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
//공통원소 구하기
public class Main {
public List<Integer> solution(int n, int m, int[] a, int[] b) {
List<Integer> answer = new ArrayList<>();
//오름차순 정렬 (a와 b 각각에 오름차순 정렬로 저장이 되어버림)
Arrays.sort(a);
Arrays.sort(b);
int p1 = 0, p2 = 0;
while (p1 < n && p2 < m) {
if(a[p1] == b[p2]) {
answer.add(a[p1++]);
p2++;
} else if (a[p1] < b[p2]) p1++;
else p2++;
}
return answer;
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = kb.nextInt();
}
int m = kb.nextInt();
int[] b = new int[m];
for (int i = 0; i < m; i++) {
b[i] = kb.nextInt();
}
for (int x : T.solution(n, m, a, b)) {
System.out.print(x + " ");
}
}
}03. 최대 매출
설명
현수의 아빠는 제과점을 운영합니다. 현수 아빠는 현수에게 N일 동안의 매출기록을 주고 연속된 K일 동안의 최대 매출액이 얼마인지 구하라고 했습니다.
만약 N=10이고 10일 간의 매출기록이 아래와 같습니다. 이때 K=3이면
12 1511 20 2510 20 19 13 15
연속된 3일간의 최대 매출액은 11+20+25=56만원입니다.
여러분이 현수를 도와주세요.입력
첫 줄에 N(5<=N<=100,000)과 K(2<=K<=N)가 주어집니다.
두 번째 줄에 N개의 숫자열이 주어집니다. 각 숫자는 500이하의 음이 아닌 정수입니다.출력
첫 줄에 최대 매출액을 출력합니다.예시 입력 1
10 3
12 15 11 20 25 10 20 19 13 15예시 입력 1
56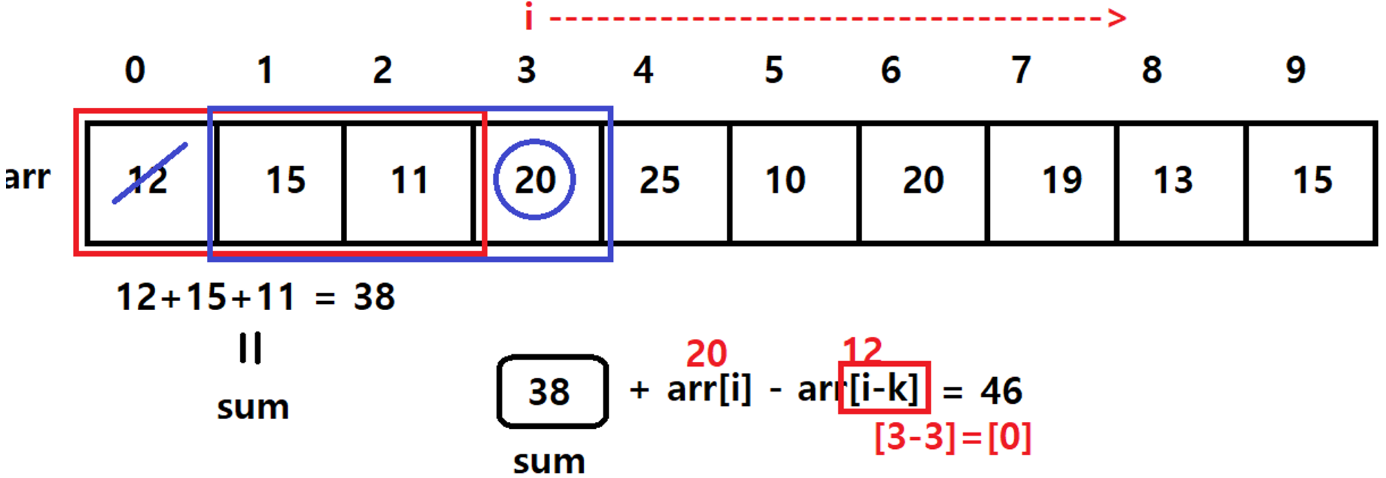
이를 "Sliding window" 라고 한다.코드
import java.util.Scanner;
// 최대 매출
public class Main {
public int solution(int n, int k, int[] arr) {
int answer = 0, sum = 0;
for (int i = 0; i < k; i++) {
sum += arr[i];
}
answer = sum;
for (int i = k; i < n; i++) {
sum += arr[i] - arr[i - k];
answer = Math.max(sum, answer);
}
return answer;
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
int k = kb.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = kb.nextInt();
}
System.out.println(T.solution(n, k, arr));
}
}04. 연속 부분수열
설명
N개의 수로 이루어진 수열이 주어집니다.
이 수열에서 연속부분수열의 합이 특정숫자 M이 되는 경우가 몇 번 있는지 구하는 프로그램을 작성하세요.
만약 N=8, M=6이고 수열이 다음과 같다면
1 2 1 3 1 1 1 2
합이 6이 되는 연속부분수열은 {2, 1, 3}, {1, 3, 1, 1}, {3, 1, 1, 1}로 총 3가지입니다.입력
첫째 줄에 N(1≤N≤100,000), M(1≤M≤100,000,000)이 주어진다.
수열의 원소값은 1,000을 넘지 않는 자연수이다.출력
첫째 줄에 경우의 수를 출력한다.예시 입력 1
8 6
1 2 1 3 1 1 1 2예시 출력 1
31차 풀이 코드
package section3;
import java.util.Scanner;
//연속 부분수열
public class ExampleFour {
public int solution(int n, int m, int[] arr) {
int answer = 0, sum = 0;
**for (int i = 0; i < n; i++)** {
sum += arr[i];
**for (int j = i + 1; j < n; j++)** { **//이중 for문을 돌게 되면 시간복잡도가 O(N^2) 이다.**
sum += arr[j];
if (sum == m) {
answer++;
sum = 0;
break;
} else if (sum > m) {
sum = 0;
break;
}
}
}
return answer;
}
public static void main(String[] args) {
ExampleFour T = new ExampleFour();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
int m = kb.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = kb.nextInt();
}
System.out.println(T.solution(n,m,arr));
}
}이중 for문을 돌게 되면 시간복잡도가 O(N^2) 이다.
여기서 입력에서 줬던 조건을 되돌아 보자.
"첫째 줄에 N(1≤N≤100,000), M(1≤M≤100,000,000)이 주어진다."
만약 N이 100,000 (십만) 그리고 M이 100,000,000 (1억) 이라고 가정해보자.
N값이 M값보다 현저히 작은 숫자를 차지하여 누적해 갈 때 스텝 수는 헤아릴 수 없이 거대해져 시간 복잡도가 굉장히 비효율적이다.
=> O(n^2) 으로는 연산이 불가능하다.Two pointers, Sliding window 는 O(n^2)으로 접근하기 쉽겠지만 O(n)으로 접근해야 한다.
최종 코드
import java.util.Scanner;
//연속 부분수열
public class Main {
public int solution(int n, int m, int[] arr) {
int answer = 0, sum = 0, lt = 0;
for (int rt = 0; rt < n; rt++) {
sum += arr[rt];
//여기서 sum은 lt부터 rt까지의 합이다.(최초 rt와 lt는 동일 인덱스 번호이기 때문)
if(sum==m) answer++;
//lt는 sum이 m보다 크거나 같을때 인덱스의 값을 sum에서 빼고, 인덱스 번호를 +1한다.
/**
* ex >만약 배열이 1 1 1 1 5라고 가정했을 때, sum은 9이다. lt의 0번 인덱스 값을 빼면 sum은 8이 되고, lt 인덱스 번호는 1번이다.
* 여전히 sum은 8로 6보다 크므로 lt 값을 빼고, 인덱스 번호를 +1 해주는 작업을 반복해야 된다.
* 그러므로 lt를 변경하는 작업을 여러번 할 수 있으므로 while문을 작성해야 한다.
*
*/
while (sum >= m) {
//lt는 후위연산자
sum -= arr[lt++];
if(sum==m) answer++;
}
}
return answer;
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
int m = kb.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = kb.nextInt();
}
System.out.println(T.solution(n,m,arr));
}
}05. 연속된 자연수의 합
설명
N입력으로 양의 정수 N이 입력되면 2개 이상의 연속된 자연수의 합으로 정수 N을 표현하는 방법의 가짓수를 출력하는 프로그램을 작성하세요.
만약 N=15이면
7+8=15
4+5+6=15
1+2+3+4+5=15
와 같이 총 3가지의 경우가 존재한다.입력
첫 번째 줄에 양의 정수 N(7<=N<1000)이 주어집니다.출력
첫 줄에 총 경우의 수를 출력합니다.예시 입력 1
15예시 출력 1
3코드-1 (선형검색 (Linear Search))
import java.util.Scanner;
//연속된 자연수의 합 (경우의 수)
//연속 부분수열 과 유사!!
public class Main{
public int solution(int n) {
int answer = 0, sum = 0, lt = 1;
for (int rt = 1; rt < n; rt++) {
sum += rt;
if (sum == n) {
answer++;
}
while (sum >= n) {
sum -= lt++;
if(sum == n) {
answer++;
}
}
}
return answer;
}
public static void main(String[] args) {
MainT = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
System.out.println(T.solution(n));
}
}코드-2 (이진검색(Binary Search))
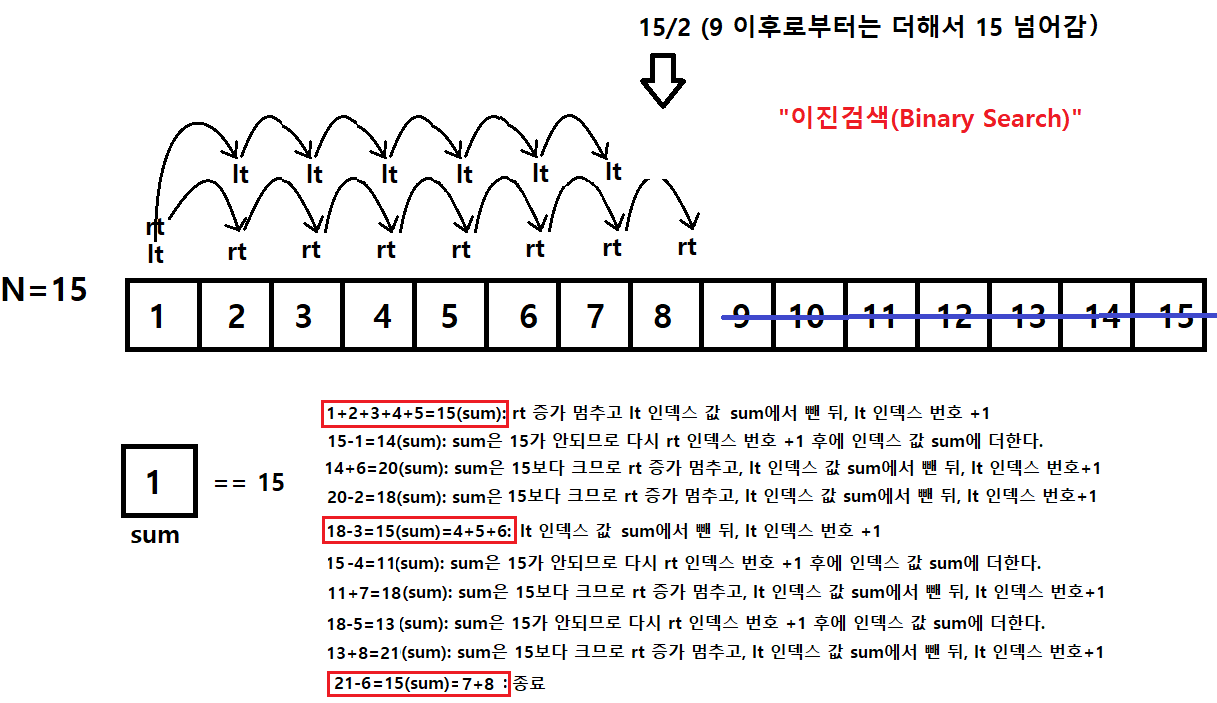
import java.util.Scanner;
//연속된 자연수의 합 (경우의 수)
//연속 부분수열 과 유사!!
public class Main {
public int solution(int n) {
int answer = 0, sum = 0, lt = 0;
int m = n / 2 + 1; //실제론 1부터 세지만 lt, for문의 i가 0으로 초기화 되어있기 때문에
int[] arr = new int[m]; //정렬된 배열
//arr에 대입한 후
for (int i = 0; i < m; i++) arr[i] = i + 1;
for (int rt = 0; rt < m; rt++) {
//arr의 값을 조건에 맞게 sum에 대입
sum += arr[rt];
if (sum == n) answer++;
while(sum>=n){
sum -= arr[lt++];
if(sum==n) answer++;
}
}
return answer;
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
System.out.println(T.solution(n));
}
}코드-3 (수학적 방법)
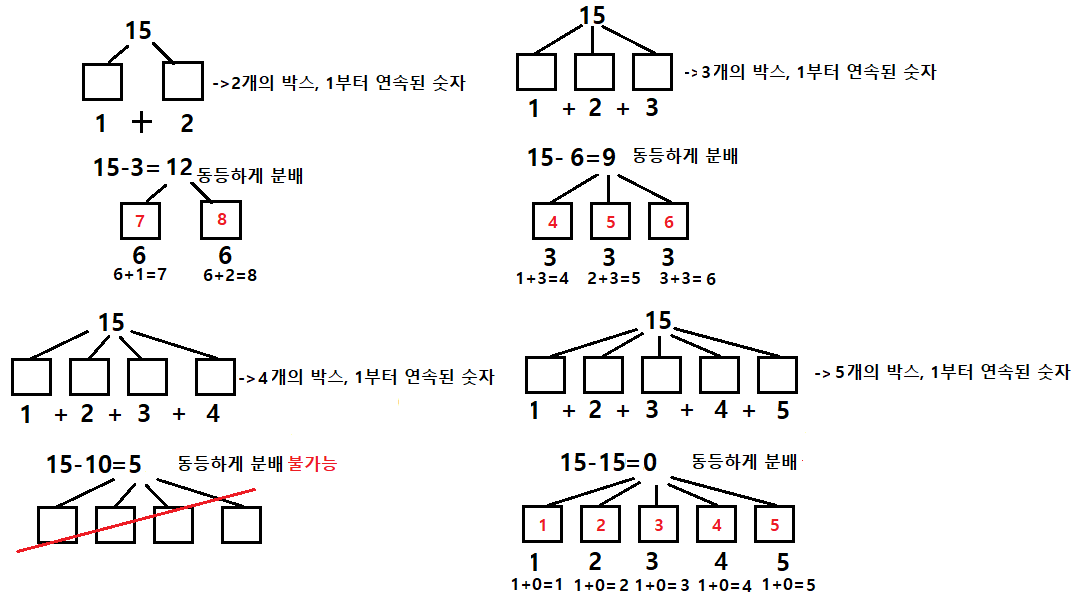
import java.util.Scanner;
//연속된 자연수의 합 (경우의 수)
public class Main{
public int solution(int n) {
int answer = 0, cnt = 1;
//n이 15라면 14로 -1
n--;
while (n > 0) {
//첫번째 while문에서 cnt가 2로 증가
cnt++;
//14인 n은 -2하여 12가 된다 (=while문 전에 1빼고, while문 안에서 2를 뺐다.)
n=n-cnt;
//n이 cnt로 나눴을때 나머지가 0이라는 것은 "연속된 자연수가 15가 된다는 것"
if (n % cnt == 0) {
answer++;
}
}
return answer;
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
System.out.println(T.solution(n));
}
}코드를 보면 그림과 달리 n이 -1 차이나고, cnt가 +1 차이나는 것을 확인할 수 있다.
하지만 이는 문제를 야기하지 않고 "동등하게 분배" 시에 그림과 동일 숫자라면 코드 흐름은 동일한 프로세스로 진행된다.06. 최대 길이 연속부분수열
설명
0과 1로 구성된 길이가 N인 수열이 주어집니다. 여러분은 이 수열에서 최대 k번을 0을 1로 변경할 수 있습니다. 여러분이 최대 k번의 변경을 통해 이 수열에서 1로만 구성된 최대 길이의 연속부분수열을 찾는 프로그램을 작성하세요.
만약 길이가 길이가 14인 다음과 같은 수열이 주어지고 k=2라면
1 1 0 0 1 1 0 1 1 0 1 1 0 1
여러분이 만들 수 있는 1이 연속된 연속부분수열은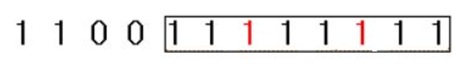
이며 그 길이는 8입니다.입력
첫 번째 줄에 수열의 길이인 자연수 N(5<=N<100,000)이 주어집니다.
두 번째 줄에 N길이의 0과 1로 구성된 수열이 주어집니다.출력
첫 줄에 최대 길이를 출력하세요.예시 입력 1
14 2
1 1 0 0 1 1 0 1 1 0 1 1 0 1예시 출력 1
8
코드
import java.util.Scanner;
//최대 길이 연속부분수열
public class Main {
public int solution(int n, int k, int[] arr) {
int answer = 0, cnt = 0, lt = 0; //left
//right
for (int rt = 0; rt < n; rt++) {
if (arr[rt] == 0) cnt++;
//cnt는 k보다 크면 안된다.
while (cnt > k) {
//lt 인덱스 값이 0이되면 cnt는 -1
if(arr[lt] == 0) cnt--;
//if문을 만날 때까지 lt를 증가
lt++;
}
//최종 1이 연속된 길이는 마지막에 대입시켜준다.
answer = Math.max(answer, rt - lt + 1);
}
return answer;
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
int k = kb.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = kb.nextInt();
}
System.out.println(T.solution(n,k,arr));
}
}