0722
문제 설명
어느 학교에 페인트가 칠해진 길이가 n미터인 벽이 있습니다. 벽에 동아리 · 학회 홍보나 회사 채용 공고 포스터 등을 게시하기 위해 테이프로 붙였다가 철거할 때 떼는 일이 많고 그 과정에서 페인트가 벗겨지곤 합니다. 페인트가 벗겨진 벽이 보기 흉해져 학교는 벽에 페인트를 덧칠하기로 했습니다.
넓은 벽 전체에 페인트를 새로 칠하는 대신, 구역을 나누어 일부만 페인트를 새로 칠 함으로써 예산을 아끼려 합니다. 이를 위해 벽을 1미터 길이의 구역 n개로 나누고, 각 구역에 왼쪽부터 순서대로 1번부터 n번까지 번호를 붙였습니다. 그리고 페인트를 다시 칠해야 할 구역들을 정했습니다.
벽에 페인트를 칠하는 롤러의 길이는 m미터이고, 롤러로 벽에 페인트를 한 번 칠하는 규칙은 다음과 같습니다.
- 롤러가 벽에서 벗어나면 안 됩니다.
- 구역의 일부분만 포함되도록 칠하면 안 됩니다.
즉, 롤러의 좌우측 끝을 구역의 경계선 혹은 벽의 좌우측 끝부분에 맞춘 후 롤러를 위아래로 움직이면서 벽을 칠합니다. 현재 페인트를 칠하는 구역들을 완전히 칠한 후 벽에서 롤러를 떼며, 이를 벽을 한 번 칠했다고 정의합니다.
한 구역에 페인트를 여러 번 칠해도 되고 다시 칠해야 할 구역이 아닌 곳에 페인트를 칠해도 되지만 다시 칠하기로 정한 구역은 적어도 한 번 페인트칠을 해야 합니다. 예산을 아끼기 위해 다시 칠할 구역을 정했듯 마찬가지로 롤러로 페인트칠을 하는 횟수를 최소화하려고 합니다.
정수 n, m과 다시 페인트를 칠하기로 정한 구역들의 번호가 담긴 정수 배열 section이 매개변수로 주어질 때 롤러로 페인트칠해야 하는 최소 횟수를 return 하는 solution 함수를 작성해 주세요.
제한사항
- 1 ≤
m≤n≤ 100,000 - 1 ≤
section의 길이 ≤n- 1 ≤
section의 원소 ≤n - section의 원소는 페인트를 다시 칠해야 하는 구역의 번호입니다.
- section에서 같은 원소가 두 번 이상 나타나지 않습니다.
- section의 원소는 오름차순으로 정렬되어 있습니다.
- 1 ≤
입출력 예
n | m | section | result |
|---|---|---|---|
8 | 4 | [2, 3, 6] | 2 |
5 | 4 | [1, 3] | 1 |
4 | 1 | [1, 2, 3, 4] | 4 |
입출력 예 설명
입출력 예 #1
- 예제 1번은 2, 3, 6번 영역에 페인트를 다시 칠해야 합니다. 롤러의 길이가 4미터이므로 한 번의 페인트칠에 연속된 4개의 구역을 칠할 수 있습니다. 처음에 3, 4, 5, 6번 영역에 페인트칠을 하면 칠해야 할 곳으로 2번 구역만 남고 1, 2, 3, 4번 구역에 페인트칠을 하면 2번 만에 다시 칠해야 할 곳에 모두 페인트칠을 할 수 있습니다.
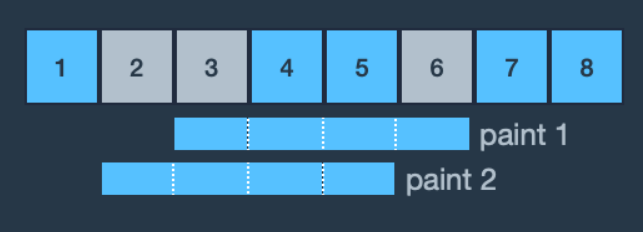2번보다 적은 횟수로 2, 3, 6번 영역에 페인트를 덧칠하는 방법은 없습니다. 따라서 최소 횟수인 2를 return 합니다.
입출력 예 #2
- 예제 2번은 1, 3번 영역에 페인트를 다시 칠해야 합니다. 롤러의 길이가 3미터이므로 한 번의 페인트칠에 연속된 3개의 구역을 칠할 수 있고 1, 2, 3번 영역에 페인트칠을 하면 한 번에 1, 3번 영역을 모두 칠할 수 있습니다.
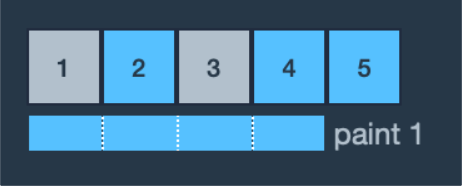따라서 최소 횟수인 1을 return 합니다.
입출력 예 #3
- 예제 3번은 모든 구역에 페인트칠을 해야 합니다. 롤러의 길이가 1미터이므로 한 번에 한 구역밖에 칠할 수 없습니다. 구역이 4개이므로 각 구역을 한 번씩만 칠하는 4번이 최소 횟수가 됩니다.
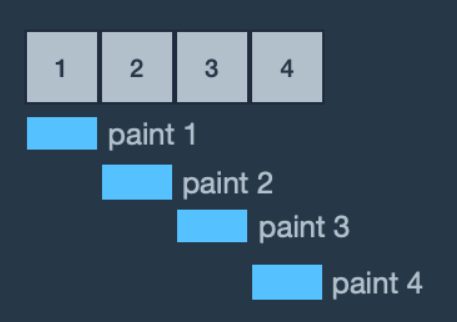따라서 4를 return 합니다.
풀이 방법
이 문제는 페인트가 벗겨진 곳을 최소한의 페인트질로 완전히 칠하는 문제입니다.
1. 나의 첫 번째 풀이
처음 저의 알고리즘은 다음과 같았습니다.
- 페인트가 벗겨진 시작부분부터 끝 부분까지의 길이를 구합니다.
- 만약 페인트가 벗겨진 부분의 길이가 페인트칠 한 번의 길이보다 작거나 같다면
1을 리턴하고 크다면 나머지값을 리턴하여 몫을 구합니다.
하지만 아래의 코드는 초반 실행결과에서는 문제가 없었지만 실행 후 제출을 하니 에러가 나며 통과되지 못 하였습니다.
그리고 곧 그 이유는 최솟값을 구하지 못하였기 때문이라는 결론을 내었습니다.
// 첫 번째 코드
class Solution {
public int solution(int n, int m, int[] section) {
int sec = section[section.length-1]-section[0]+1;
return sec/m+(sec <= m ? 1 : sec%m);
}
}2. 나의 두 번째 풀이(정답)
따라서 저는 알고리즘을 다음과 같이 수정하였습니다.
- 현재 벽의 숫자를 저장합니다.
- 칠해야 하는 벽의 숫자를 하나씩 가져옵니다.
- 만약 현재 벽에서 페인트를 칠했을 때 칠해야 하는 벽의 숫자보다 작다면 칠하는 숫자를
1증가시킨 후, 현재 벽을 현재 페인트를 칠해야 하는 벽의 숫자로 변경시킵니다.
말로만 들으니 잘 이해가 가지 않죠?
한 번 코드와 함께 이해해봅시다.
public int solution(int n, int m, int[] section) {
int answer = 1;
int start = section[0];n은 전체 벽의 길이를 의미합니다.
m은 페인트칠을 한 번 했을 때 칠해지는 칸 수를 의미합니다.
section은 페인트칠이 벗겨진 벽들을 담고 있습니다.
answer에는 칠해야하는 페인트질의 횟수의 최솟값을 넣을 것입니다.
무조건적으로 한 번은 페인트를 칠해야 하므로 1로 초기값을 주었습니다.
start에는 페인트칠을 시작할 기준 벽을 넣습니다.
처음이니 당연히 section[0]을 지정해줍니다.
for ( int item : section ) {
if ( start + m <= item ) {
answer++;
start = item;
}
}
return answer;이 문제의 핵심 부분인 해야하는 페인트칠의 최소 횟수를 구하는 부분입니다.
먼저 칠해야 하는 벽을 향상된 for문을 통해 각각을 item으로 가져옵니다.
만약 start + m이 item보다 작거나 같다면 페인트칠의 횟수를 1증가시킨 뒤 start를 item으로 다시 잡아줍니다.
한 번 실행 예시 1번을 가지고 코드를 다시 한 번 이해해봅시다.
answer은 초반에 1입니다. 미리 페인트칠이 한 번 되었다고 가정을 하는 것입니다.
start는 초반에 1입니다.
칠해야 하는 벽인 item은 2입니다.
01
start부터 m만큼 페인트칠을 하게 되었을 때 칠해야 하는 벽인 item보다 더 많이 칠해집니다.
즉, 2는 이미 칠해졌기 때문에 (answer의 초깃값이 1인 이유)
페인트칠은 건너뛰게 됩니다.
02
item은 그 다음으로 칠해야 하는 벽인 3으로 바뀝니다.
start부터 m만큼 페인트칠을 하게 되었을 때, 여전히 칠해야 하는 벽인 item보다 더 많이 칠해집니다.
이는 첫 번째로 칠한 페인트의 범위 내에 3이 들어가, 벽이 칠해졌다는 말입니다.
따라서 이번에도 페인트칠은 건너뛰게 됩니다.
03
마지막으로 item이 6으로 바뀝ㄴ디ㅏ.
start부터 m만큼 페인트칠을 하게 되었을 때, 이제는 start+m보다 6이 더 큽니다.
이는 아직 6번째 벽은 페인트가 칠해지지 않았다는 것이기 때문에 if문 안으로 들어가 페인트칠 횟수를 1증가시킨 뒤 기준값인 start를 item으로 변경해줍니다.
이렇게 문제가 해결되었습니다!
소스 코드
class Solution {
public int solution(int n, int m, int[] section) {
int answer = 1;
int start = section[0];
for ( int item : section ) {
if ( start + m <= item ) {
answer++;
start = item;
}
}
return answer;
}
}실행 결과
