회귀분석

회귀분석

• 회귀 분석은 실젯값과 예측값의 차이를 기반으로 한 지표들을 중심으로 성능평가지표가 발전
• 실젯값과 예측값의 차이를 구해서 이것들을 단순히 합하게 되면 +와 -가 섞여 오류를 상쇄할 수 있다.

MAE (Mean Absolute Error)

• 실젯값과 예측값의 차이를 절댓값으로 변환해 평균한 것
• 에러의 크기가 그대로 반영
• 이상치에 영향을 받는다.

MSE (Mean Squared Eroor)

• 실젯값과 예측값의 차이를 제곱해 평균한 것
• 실젯값과 예측값 차이의 면적 합을 의미
• 특이값이 존재하면 수치가 증가

RMSE (Root Mean Squared Error)

• 실젯값과 예측값의 차이를 제곱해 평균한 것에 루트를 씌운것
• 에러에 제곱을 하면 에러가 클수록 그에 따른 가중치가 높이 반영
• 손실이 기하급수적으로 증가하는 상황에서 실제 오류평균보다 값이 더 커짖 않도록 상쇄하기 위해 사용

MSLE (Mean Squared Log Error)

• 실젯값과 예측값의 차이를 제곱해 평균한 것에 로그를 적용한 것
• RMSE와 같이 손실이 기하급수적으로 증가하는 상황에서 실제 오류평균보다 값이 더 커지지 않도록 상쇄하기 위하여 사용

MAPE (Mean Absolute Percentage Error)

• MAE를 퍼센터로 변환한 것
• 오차가 예측값에서 차지하는 정도를 나타냄

import pandas as pd

boston = pd.read_csv("data/boston.csv", encoding='utf-8')
boston.head()

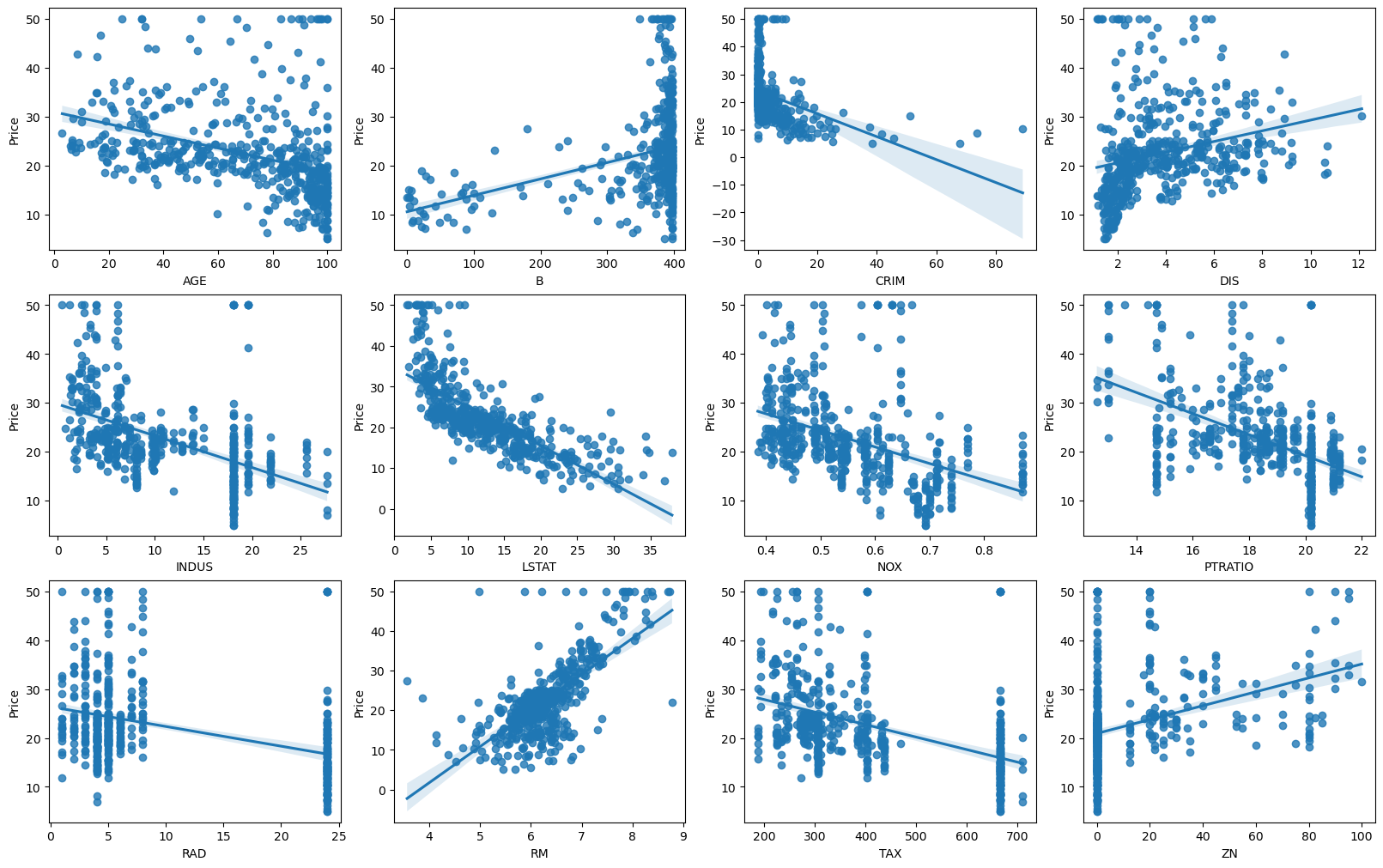
## 산점도와 선형 회귀직선 시각화

import matplotlib.pyplot as plt 
import seaborn as sns

fig, axs = plt.subplots(figsize=(16, 10), ncols = 4, nrows = 3,constrained_layout = True)
features = boston.columns.difference(['Price', 'CHAS'])

for i, feature in zip(range(12), features):
    row  = int(i/4)
    col = i%4
    sns.regplot(x = feature, y = boston['Price'], data=boston, ax=axs[row][col])

## 데이터 분할
from sklearn.model_selection import train_test_split

x = boston[['CRIM', 'ZN', 'INDUS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']].values
y = boston['Price'].values

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state = 42)

print("학습데이터세트 price 평균 :", y_train.mean())
print("평가데이터세트 price 평균 :", y_test.mean())

## 데이터 전처리 
## 비율, 농도, 개수 등 서로 다른 단위를 가진 연속형 자료
## Min-Max 방법으로 정규화 과정
from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()
x_train_sc = scaler.fit_transform(x_train)

## 모델 학습
## linearRegression(선형 회귀) 알고리즘
from sklearn.linear_model import LinearRegression
linear = LinearRegression()
linear.fit(x_train_sc, y_train)

from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.metrics import r2_score
import numpy as np

## predict()로 학습데이터를 예측한 값을 저장
pred_train = linear.predict(x_train_sc)

mae = mean_absolute_error(y_train, pred_train)
mse = mean_squared_error(y_train, pred_train)
rmse = np.sqrt(mse)
## 결정계수 출력
r2 = r2_score(y_train, pred_train)

print('MAE: {0: .5f}'.format(mae))
print('MSE: {0: .5f}'.format(mse))
print('RMSE: {0: .5f}'.format(rmse))
print('R2: {0: .5f}'.format(r2))

## 모델의 설명력은 74.5%로 양호하게 출력됨
## MAE를 통하여 pred_train, y_train은 평균 3.32 정도 차이를 보인다.

## 성능평가 및 예측값 저장
## x_test를 scaler.transform()에 입력하여 x_train과 같은 방식으로 Min-Max 정규화를 수행
## x_test_sc를 훈련된 모델에 입력해 예측값을 pred에 저장

x_test_sc = scaler.transform(x_test)
pred = linear.predict(x_test_sc) 

mae = mean_absolute_error(y_test, pred)
mse = mean_squared_error(y_test, pred)
rmse = np.sqrt(mse)
r2 = r2_score(y_test, pred)
print('MAE: {0: .5f}'.format(mae))
print('MSE: {0: .5f}'.format(mse))
print('RMSE: {0: .5f}'.format(rmse))
print('R2: {0: .5f}'.format(r2))

## pred와 y_test를 비교하여 선형 회귀 모델의 예측성능을 평가
## 모델의 설명력은 66.4%
## MAE를 통하여 pred와 y_test는 평균 3.23 정도의 차이를 보인다.