[혼공머신] 2주차_ k-최근접 이웃 회귀

💡 지도학습

① 분류 : 샘플을 몇 개의 클래스 중 하나로 분류 ex) 도미와 빙어

▶ "k-최근접 이웃 분류" 알고리즘

• KNeighborsClassifier 라는 사이킷런 클래스 이용
• 예측하려는 샘플에 가장 가까운 샘플 k개를 선택 (ex.3개)
• 샘플들의 클래스를 확인하여 다수 클래스를 새로운 샘플의 클래스로 예측(ex.△△□ 이면 샘플의 클래스는 △)

② 회귀 : 임의의 어떤 숫자를 예측 즉, 두 변수 사이의 상관관계를 분석하여 어떤 숫자를 예측하는 것. ex) 배달이 도착할 시간 예측, 내년 경제 성장률 예측

▶ "k-최근접 이웃 회귀" 알고리즘

• KNeighborsRegressor 라는 사이킷런 클래스 이용
• 이웃샘플의 타깃값의 평균을 예측 타깃값으로 사용
• 결정계수로 타깃의 평균정도를 예측하는지 확인(0에 가까우면 타깃의 평균정도이고 1에 가까우면 타겟에 가깝게 예측한 것.)
• 타깃값과 예측값의 평균 절댓값 오차 계산
• 과대/과소 적합인 경우 모델을 덜 복잡하게 또는 더 복잡하게 만들어서 해결.

1) 농어 길이와 무게 데이터 파악

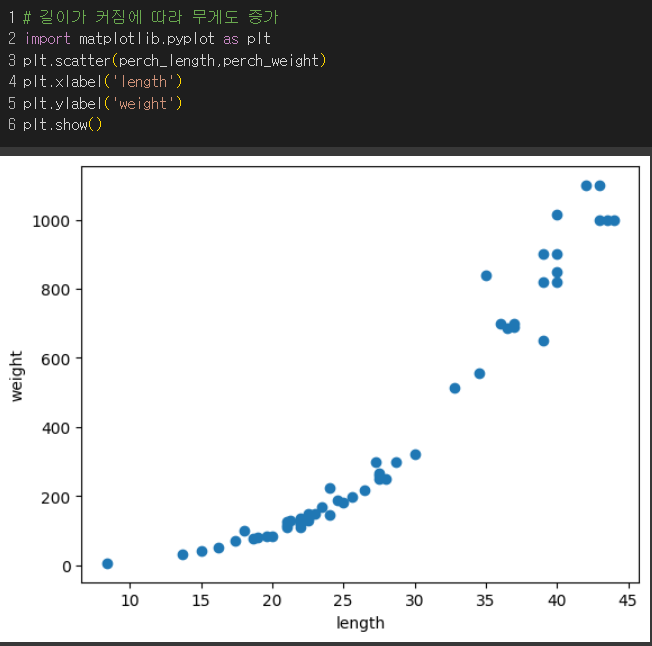
길수록 무거워짐!

2) train과 test set으로 나눈 후 사이킷런을 이용하기 위해 2차원 배열로 만들기

3) 모형 훈련 후 결정계수(점수)로 타깃의 평균정도를 예측하는지 확인

▶ 결정계수 = 1 - $\frac{(타깃-예측)^2의 합}{(타깃-평균)^2의 합}$

• 타깃의 평균 정도를 예측하면 분수가 1이 되어 결정계수가 0에 가까워짐.
• 예측이 타깃에 아주 가까워지면 분수가 0이 되어 결정계수가 1에 가까워짐. (good👍)
  
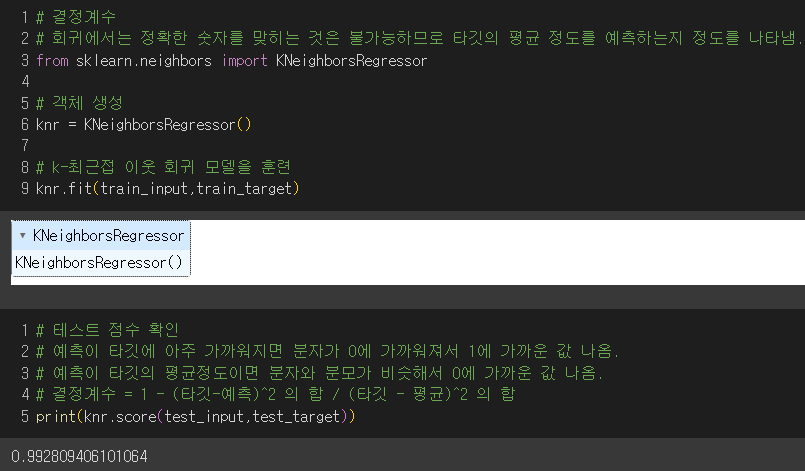
  결과 : 예측한 값이 타깃에 가까워서 결정계수가 높음.👍

4) 타깃과 예측한 값의 절댓값 오차를 평균하여 어느 정도 예측이 벗어났는지 알아보기

결과 : 예측한 값이 평균적을 19g정도 타깃값과 다르다.

✔️ 과대적합, 과소적합

• 과대적합 : 훈련 세트의 점수는 높은데 테스트 세트의 점수가 안 좋은 경우/ 훈련세트에만 잘 맞는 모델

→ 해결책 : 모델을 덜 복잡하게 만들면 됨.

• 과소적합 : 훈련 세트의 점수보다 테스트 세트의 점수가 높거나 두 점수 모두 너무 낮은 경우/ 모델이 너무 단순하여 훈련세트에서 적절하게 훈련되지 않은 경우/ 훈련세트와 테스트 세트의 크기가 작으면 일어날 수 있음.

→ 해결책 : 모델을 더 복잡하게 만들면 됨.

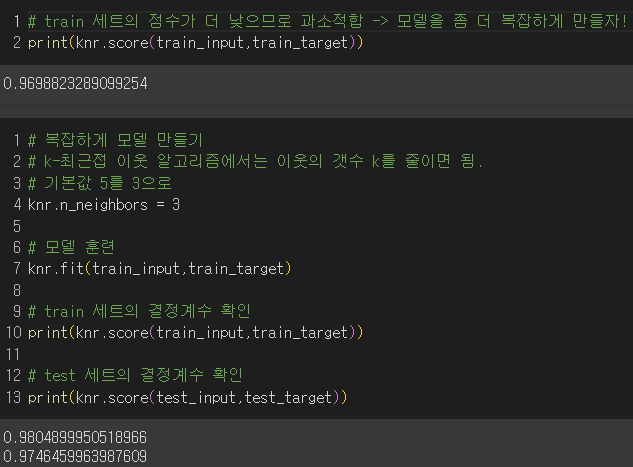
결과 : 최적의 k값을 찾는 방법은 5장에서!
이웃의 개수를 줄임으로써 모델을 더 복잡하게 만들어서 테스트 세트의 점수가 훈련 세트의 점수보다 낮아졌으므로 과소적합 문제 해결

미션

p.128 확인문제 2
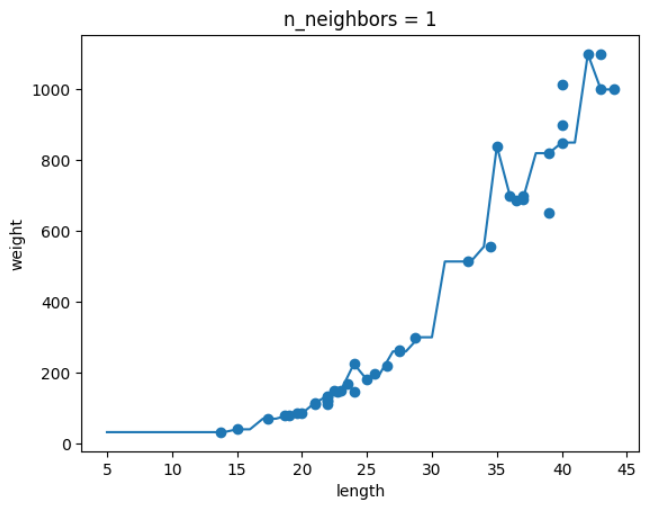
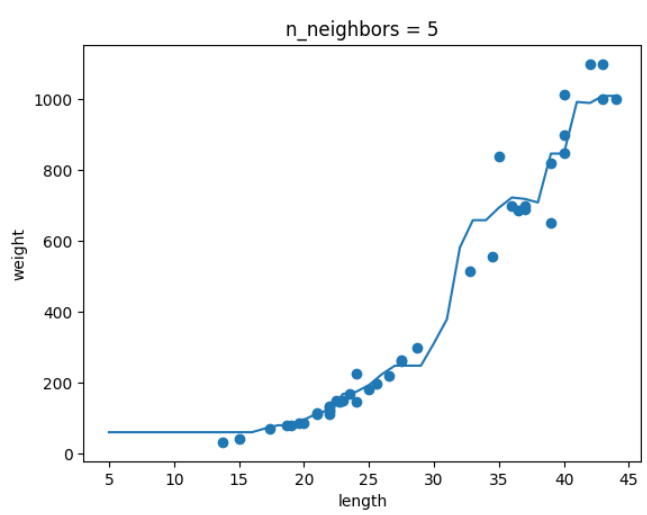
k-최근접 이웃 회귀 모델의 k값을 1,5,10으로 바꿔가면서 훈련하고, 농어의 길이를 5에서 45까지 바꿔가면서 예측을 만들어 그래프로 나타내기

• k=1 일때
  

• k=5 일때
  

• k=10 일때
  

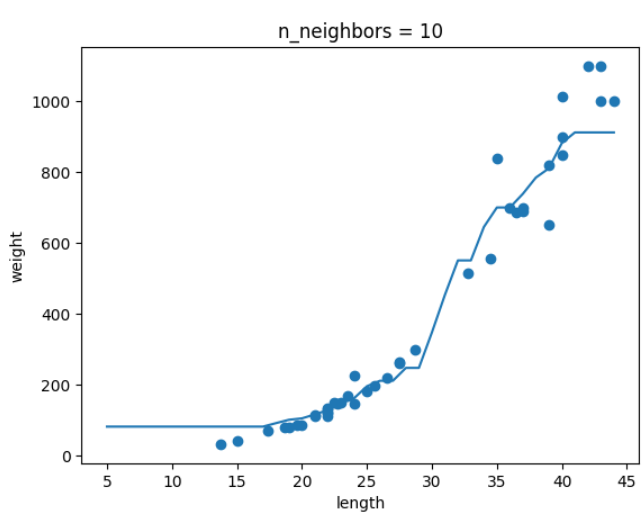
결론 : k가 커지면서 그래프가 smooth해지는 것을 보아 모델이 단순해지는 것을 알 수 있다.

👎 한계 : 훈련 세트 범위 밖의 값을 예측하지 못함.

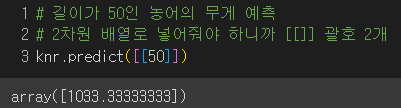
실제로 산점도에 표현해보니

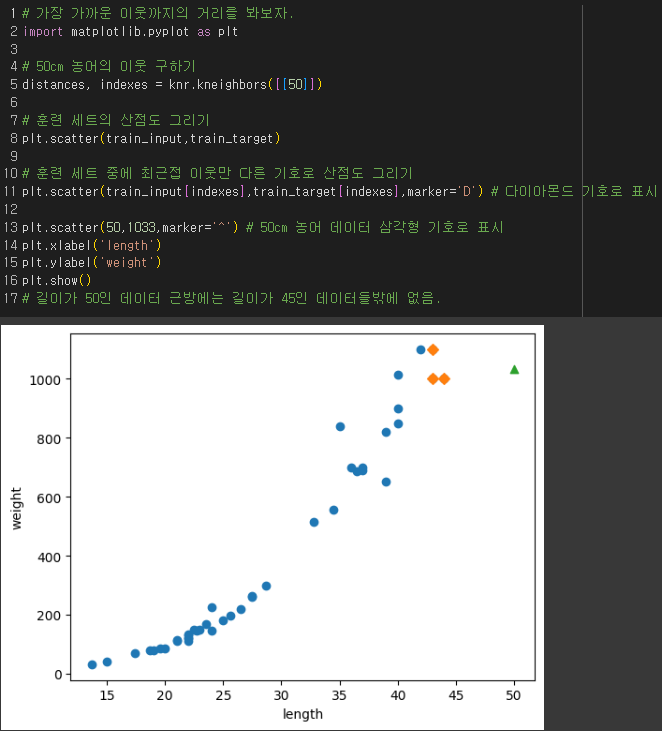
이웃 한 점들이 너무 동떨어져 있었고

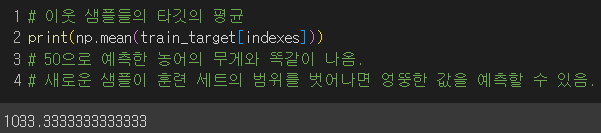
이웃한 샘플의 타깃값의 평균을 예측 타깃값으로 사용하다보니 길이가 50에서나 100에서나 똑같은 값을 출력해준 것.

→ 해결책 :

• 시간과 환경의 변화를 반영하여 새로운 데이터로 반복적으로 k-최근접 이웃 모델을 학습해줄것.
• 선형회귀 알고리즘 이용

▶ 선형회귀

• 특성이 하나일 때 그 특성을 가장 잘 나타낼 수 있는 직선을 찾는 알고리즘
• LinearRegression 클래스 이용
  
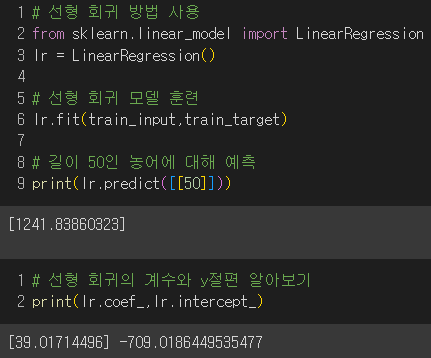
  최적의 모델 파라미터를 찾아 나온 회귀선 :

  무게 = 39 * 길이 - 709

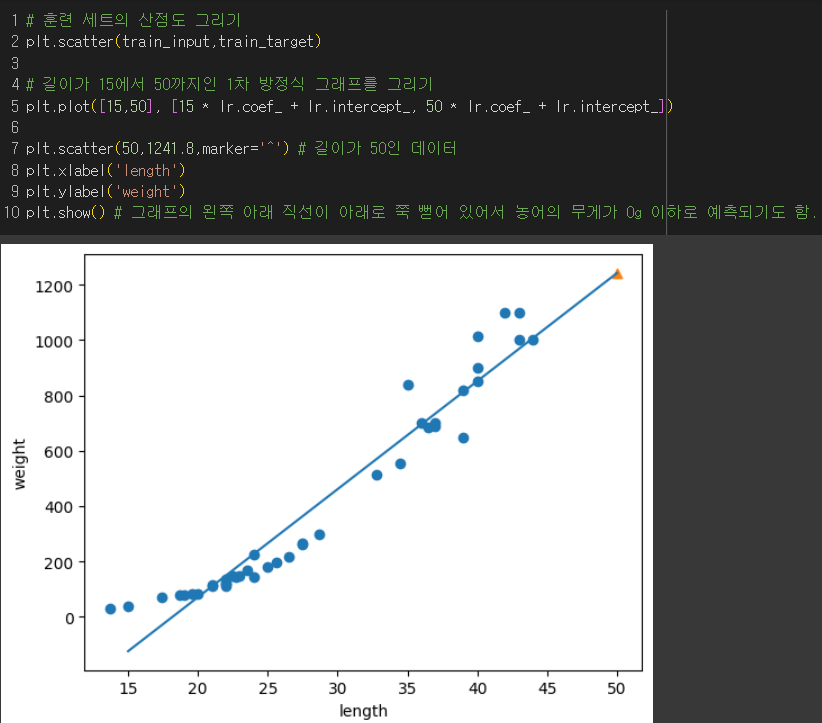
👎그래프의 왼쪽 끝부분을 보면 농어의 무게가 0g이하로 예측될 때도 있음.

👎과소적합의 문제도 있음.

→ 해결책 : 농어의 길이와 무게에 대한 산점도를 보면 왼쪽 아래 부분이 곡선에 가까우므로 최적의 곡선을 찾아보자.

▶ 다항회귀 : 다항식을 사용한 선형회귀
길이의 제곱항 추가 후 모델 훈련

주의점 :

• np.column_stack()은 튜플로 전달해야 해서 괄호를 2개써야함!
• 2차원으로 만들어진 데이터셋인지 확인

최적의 모델 파라미터를 찾아 나온 회귀선 :

무게 = 1.01 * 길이*길이 - 21.6 * 길이 +116.05

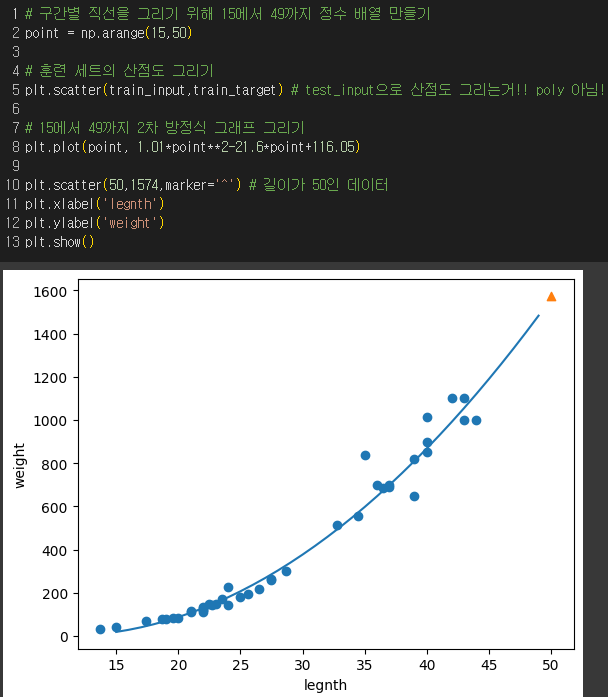
결과 : 훈련 세트보다 테스트 세트의 점수가 더 높게 나와서 과소적합이므로 모델을 더 복잡하게 하여 적합시켜봐야함!

→ 해결책 : 농어의 길이뿐만 아니라, 높이와 두께를 다항 회귀에 함께 적용해보자!

▶ 다중회귀 : 여러 개의 특성을 사용한 선형회귀
▶ 특성공학 : 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업
ex) 농어길이 * 농어높이

1) 판다스로 데이터프레임 가져온 후 넘파이로 변환 후 훈련세트와 테스트 세트로 나누기

2) PolynomialFeatures 클래스를 통해 각 특성을 제곱한 항을 추가하고 특성끼리 서로 곱한 항을 추가

• transform한 결과를 보면 각 성분끼리의 곱값과 제곱값이 들어가있는 걸 볼 수 있음.
  주의점 : 절편은 항상 값이 1인 특성과 곱해지는 계수이고 사이킷런은 자동으로 절편을 추가해주므로 1은 필요없음. → include_bias=False

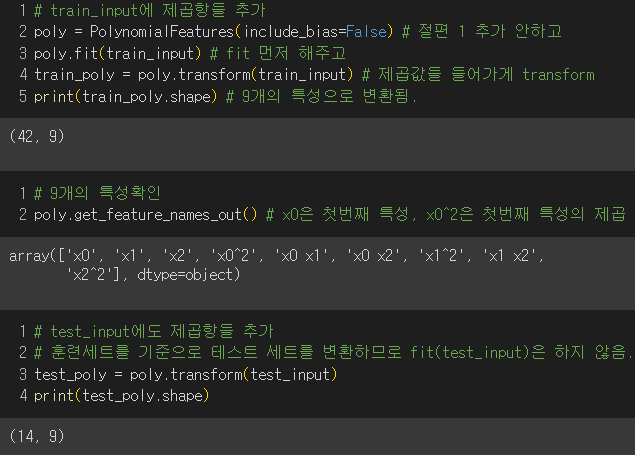
• 테스트 세트도 똑같이 진행해주면 됨!

3) 다중 회귀 모델 훈련

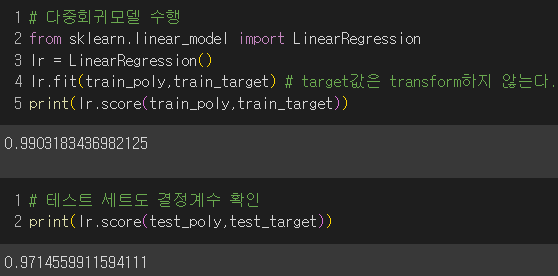
4) degree 매개변수를 통해 고차항의 최대개수 늘려보기

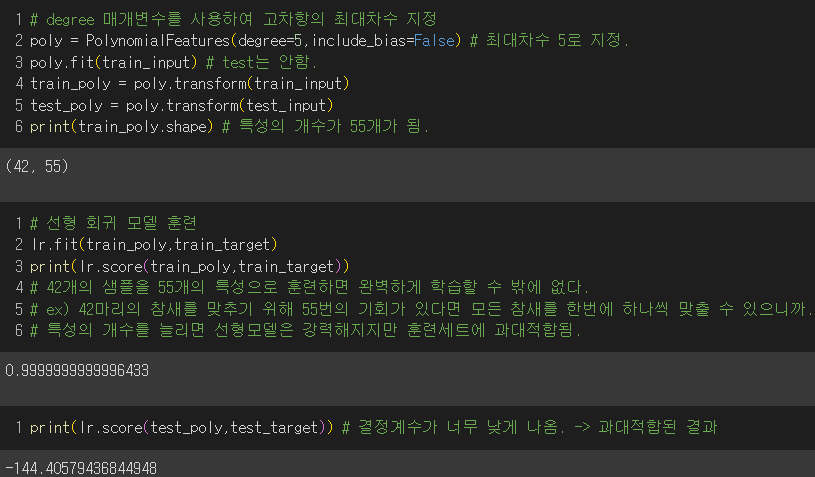
• 훈련세트에 과대적합되어 결정계수가 매우 낮게 나옴. 즉, 최대차수를 5로 지정하여 특성의 개수가 55개가 되었는데 훈련 세트의 샘플은 42개이므로 과대적합된 것.

▶ 규제 : 머신러닝 모델이 훈련 세트를 과도하게 학습하지 못하도록 하는 것.
ex) 선형회귀에서는 계수의 크기를 작게 하는것.

5) 곱해지는 계수의 값이 차이가 없도록 특성의 스케일을 정규화

6)
① 릿지 회귀 : 계수를 제곱한 값을 기준으로 규제를 적용

55개라는 많은 특성을 사용했는데도 과대적합되지 않았음.

alpha ↑ : 규제 강도 세지고 계수값을 더 줄이고 과소적합 되도록 유도
alpha ↓ : 계수를 줄이는 역할이 줄어들고 과대적합될 가능성 커짐.

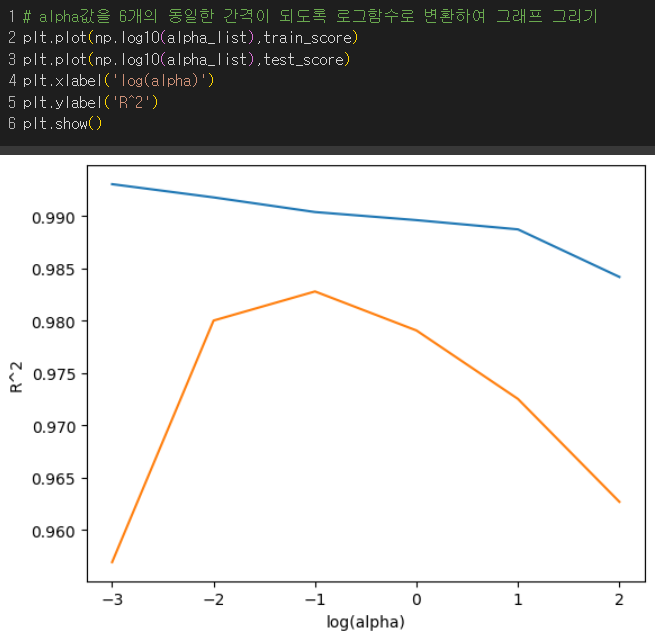
그래프에 6개의 동일한 간격의 값으로 나타나도록 log(alpha)를 x축으로 지정
결과 : (훈련세트가 파랑, 테스트 세트가 주황) 왼쪽에서는 과대적합, 오른쪽에서는 과소적합이며 두 그래프가 가장 가깝고 테스트 점수가 가장 큰 -1 즉, alpha가 0.1일때에 대해 모델을 훈련시켜보자.

👍

② 라쏘 회귀 : 계수의 절댓값을 기준으로 규제를 적용하며 계수의 크기를 아예 0으로 만들 수 있음.

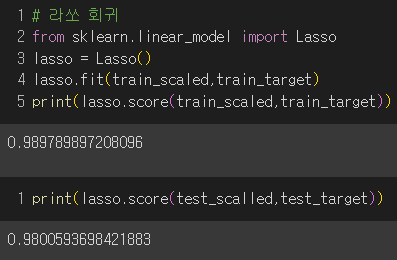
괜찮은 결과를 보여줬지만 alpha를 통해 규제 강도를 조절해보면

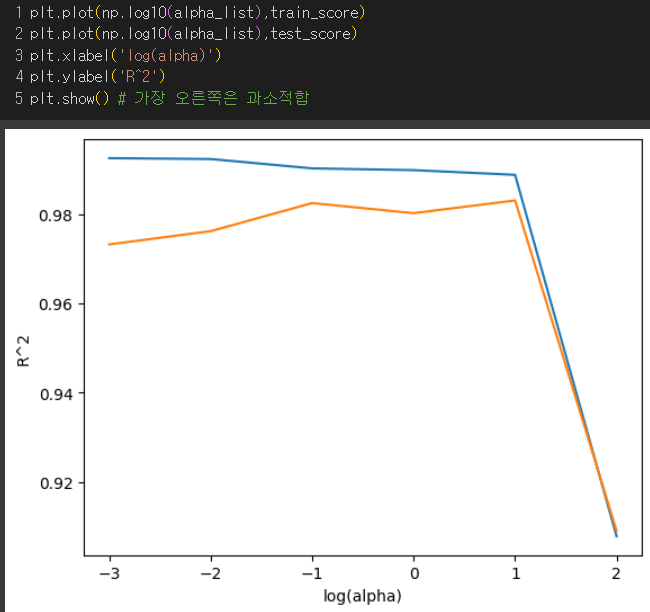
결과 : (훈련세트가 파랑, 테스트 세트가 주황) 왼쪽은 과대적합, 오른쪽은 점수가 크게 떨어지면서 과소적합 그러므로 라쏘에서 최적의 log(alpha)=1이므로 alpha = 10

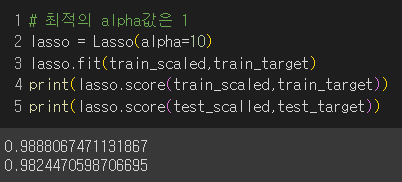
테스트 세트의 성능이 높아짐.

라쏘 모델의 계수 중 0인 것의 개수?

55개의 특성을 사용했는데 그 중 40개가 0이므로 15개의 특성만 사용함.
💡라쏘는 유용한 특성을 골라내는 데에도 쓰임!

선택미션

파라미터

• 모델 파라미터 : 머신러닝 모델이 학습 알고리즘을 통해 데이터를 추정 또는 학습한 파라미터/머신러닝 모델의 성능이 파라미터에 의해 결정됨.
  ex) 인공신경망의 가중치, SVM의 서포트 벡터, 선형 회귀에서의 결정계수, 데이터의 평균, 분산, 표준편차 등

• 하이퍼 파라미터 : 경험, 데이터의 특성 등을 고려하여 사용자가 설정한 값
  ex) k- 최근접 이웃 방법에서 최근접 이웃의 개수 k, 경사하강법에서 학습률, 에포크 수