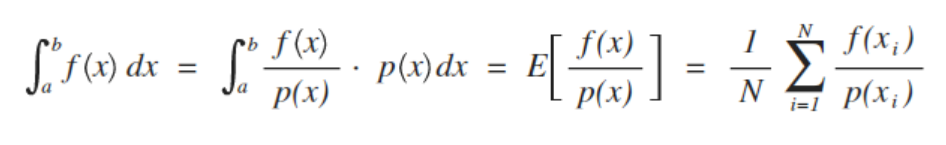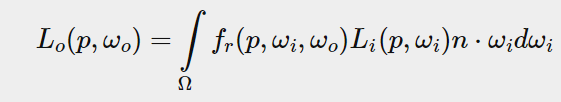적분

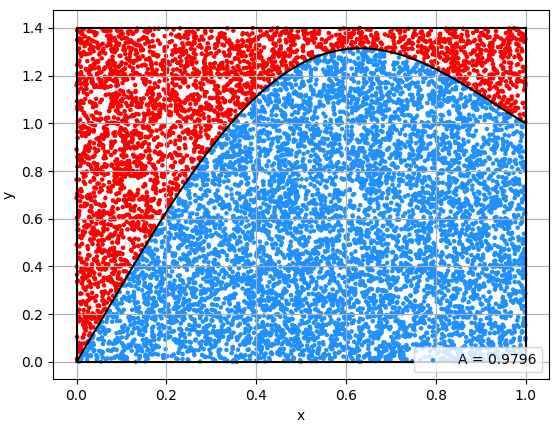
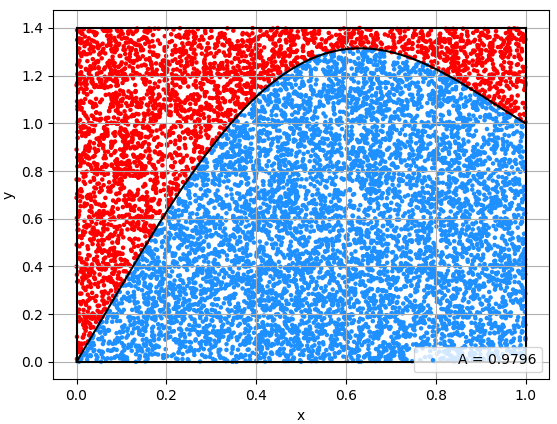
적분은 함수의 그래프가 이루는 면적을 계산하는 과정을 의미한다.

몬테 카를로 적분?

위키피디아 << 링크
몬테 카를로 적분은 간단히 정리하자면 확률이론을 이용해서 복잡한 식의 적분값을 근사하는 적분 방법이다. 왜 이름이 몬테-카를로 인지 궁금해서 위키를 읽어봤는데, 맨해튼 프로젝트에 이 적분 방식을 사용하던 수학자 니콜라스 메트로폴리스씨가 프랑스 모나코의 '몬테 카를로' 라는 도박도시의 이름에서 영감을 얻어 제안했다고 한다. 몬테 카를로 적분 = 확률로 적분값 맞추기, 도박 = 확률로 돈 따기 뭔가 적절한 이름인 것 같다.

공식

일반적인 적분을 확률 변수 $f(x)/p(x)$ 와 확률 $p(x)$의 곱으로 보고 몇개의 샘플을 뽑아서 확률변수 $f(x)/p(x)$의 평균을 이용해 적분을 근사한다.

그래픽스에서의 응용

PBR 렌더링이나 Ray Tracing에서는 모든 각에서 특정 Point에 들어오는 radiance와 그에 의해 특정 각으로 나가는 radiance가 위와 같은 적분 방정식으로 정의되어 있다. 이러한 적분값을 근사하는데 몬테 카를로 적분을 이용할 수 있다.

구분구적법과의 차이

근데 잘 생각해보면, 몬테카를로 적분말고도 컴퓨터가 사용할 수 있는 적분방식이 하나 더 있다. 구분 구적법이다. 이 방식 또한 특정 샘플 개수 만큼만으로 가로축을 분할해서 계산하면 적분값을 근사할 수 있다. 그렇다면, 그래픽스에서 몬테-카를로 방식을 굳이 써야 할까?

써야한다.. 다른 블로그 글에 따르면, 몬테 카를로 방식은 차원이 변화해도 오차값이 변함없지만, 구분구적법은 차원이 변화하면 오차가 차원에 지수적으로 증가한다고 한다. 3차원 이상부터 몬테-카를로 방식이 이점이 있다는데, 렌더링 방정식은 최소 3차이상의 방정식이니 몬테-카를로 방식을 쓰는 것이다.