개요
최근 그래픽스 공부를 열심히 하는 중인데, 렌더링 알고리즘에 쓰이는 BRDF의 의미를 어느정도 이해했다고 판단해서 정리용으로 이 글을 작성한다.
BRDF?
BRDF는 렌더링 방정식에 쓰이는 항이다.
BRDF는 Bidirectional Reflectance Distribution Function의 약자이다. 다음 자료는 PBR의 반사 방정식이다.
이 항이 BRDF다. 이 반사 방정식에 대해서도 할 말이 많지만, 그건 다음 글에서 작성하기로 하고 이 글에서는 일단 BRDF함수인 에만 집중해서 보겠다.
BRDF의 입력과 출력
BRDF는 function으로 끝나는 단어이니 당연히 함수라고 할 수 있다. 함수의 특징은 특정 인풋을 받으면 그에 해당하는 아웃풋을 뱉는다는 것을 우리는 이미 알고 있다.
BRDF는 인풋으로 (빛을 받는 좌표), (입사각), (반사각)을 받고 아웃풋으로 점에 각도의 빛을 쏘였을 때 각도로 얼마나 빛이 반사되는지가 결과값으로 나온다. 정확히 말하자면 입사각에 대해서 해당 반사각으로 반사될 확률이 나온다. 확률에 대한 분포가 반환되기 때문에 distribution function이 이름에 포함되어있다.
PBR에서 BRDF를 쓰는 이유
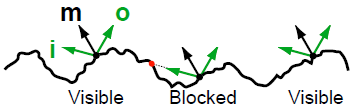
PBR(Physically Based Rendering)에서는 현실을 표방한 렌더링을 추구한다. 따라서 빛이 반사되는 것 또한 현실적으로 계산을 할 필요가 있다.
현실에서의 빛의 반사를 생각해보자, 거울과 같은 재질은 빛을 거의 완전히 반사시켜서 보여주지만 나무판자 같은 재질은 빛을 거의 반사하지 않는다. 또한 금속인 것은 딱 보면 뭔가 금속처럼 보인다. 그 이유는 표면이 거친정도(Roughness),금속인 정도(metalness), 미세면 그림자같은 물리적 요소 때문이다. BRDF는 함수내에서 이 3가지 물리법칙을 고려해서 물리적인 반사효과를 계산하기 때문에 PBR에서 사용된다.
BRDF의 실제 예(Cook-Torrance BRDF)
Cook-Torrance BRDF는 cook이라는 사람이랑 torrance라는 사람이 열심히 노력해서 만든 BRDF다.
는 입사된 빛 중에서 반사되는 빛 에너지, 는 입사된 빛 중에서 굴절되는 빛 에너지이다.
는 diffuse빛 계산을 위한 상수고 는 specullar빛 계산을 위한 함수이다. 이때 diffuse빛 계산을 위해 상수를 때려넣는 이유는 real-time에 실행하기 위해 계산을 간소화한 것이다. 다른 BRDF에서는 diffuse계산에 다른 함수를 쓰기도 한다고 한다. 하지만 상수를 때려넣는 것도 충분히 물리적으로 효과적인 계산을 할 수 있다고 한다.
cook-torrance식을 자세히 보자, 각 변수의 의미는 다음과 같다.
: Normal istribution Function (roughness값에 의한 반사 분포)
: resnel Equation(다른 각도로 봤을 때 달라지는 반사 정도)(금속성과 관련이 큼)
: eometry Function(미세면 그림자)
: 빛이 나가는 각도
: 빛이 들어온 각도
: 법선벡터
분모: 에너지 보존을 위해 나눠주는 수치
이 식에 사용되는 D,F,G는 여러가지 버전이 있을 수 있다. 어떤 사람은 계산속도를 중시해서 만들것이고 어떤 사람은 물리적으로 사실적인가를 중시해서 만들것이기 때문이다. 이 글에서는 Unreal Engine4에서 채택한 D,F,G를 조금 더 분석해보겠다. D는 Trowbridge-Reitz GGX,F는 Fresnel-Schlick approximation, G는 Smith's Schlick-GGX이다.
D : Trowbridge-Reitz GGX
이 함수는 3가지 값을 인풋으로 받는다.
: 법선 벡터
: half way벡터(참고)
: roughness수치
그리고 아웃풋은 specular빛의 분포를 나타낸다.

roughness값이 클수록 highlight되는 영역이 넓어지면서 희미해짐을 확인 할 수 있다.
F : Fresnel-Schlick approximation
일단 프레넬 방정식의 개념을 알아보자.
우리는 물 표면을 볼 때 가까운 물은 바닥까지 잘보이고 먼 물은 거울처럼 반사되어 보이는 것을 본능적으로 알고있다. 이 현상이 발생하는 이유는 빛은 다른 매질과 충돌할 때 일정 비율은 굴절이되고 일정 비율은 반사가 되는데, 입사각에 따라서 그 굴절과 반사의 비율이 달라지기 때문이다. 때문에, 입사각이 작은 가까운 물은 굴절이 많이 발생하는 것이고 입사각이 큰 먼 물은 반사가 많이 발생하는 것이다. 이 현상이 발생하는 근본적인 이유는 빛의 편광과 관련되어 있는데, 거기까지는 보지 않겠다. 중요한 것은 입사각에 따라 반사,굴절의 정도가 달리지는 현상이 존재하고 이를 표현한 것이 프레넬 방정식이라는 것이다.
프레넬 방정식은 직접 계산하기에 매우 복잡해서 PBR에서는 근사화한 버전을 사용한다(Schlick approximation).
이 함수는 3가지 인풋을 받는다.
: half way벡터
: view 벡터
: 매질의 기본 반사율
그리고 아웃풋은 프레넬 방정식에 의해 정의되는 반사율이 된다.
G : Smith's Schlick-GGX
Geometry함수는 미세면의 그림자를 나타내는 함수다. 형태는 다음과 같다.
이 함수는 3가지 인풋을 받는다.
: 법선 벡터
: view 벡터
: roughness값의 remapping(direct light,IBL등 경우에 따라 다름)
그리고 아웃풋은 얼마나 미세면 그림자가 져있는지가 나온다.

결론
BRDF는 특정 입사각과 반사각에 대해서 빛이 반사되는 정도에 대한 분포를 나타내는 함수이며, 세부적으로는 Normal Distribution Function, Fresnel Function, Geometry Function의 곱으로 정의되어 있다.
BRDF는 PBR의 핵심이며 구현자의 의도에 따라 여러가지 버전이 존재한다.




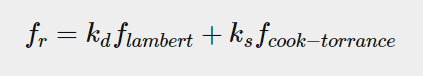
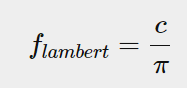
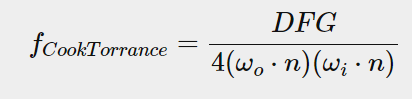



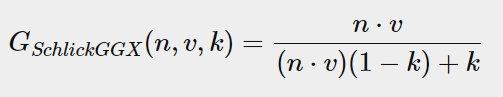
그래픽스는 독학이 거의 불가한 분야인데 출처가 하나도 남아잇지 않네요