Medium
You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).
DAG의 노드 개수를 나타내는 양의 정수 n이 주어집니다.
You are also given a 2D integer array edges, where edges[i] = [fromi, toi] denotes that there is a unidirectional edge from fromi to toi in the graph.
또한, 2차원 정수 배열 edges가 주어지는데, 여기서 edges[i] = [fromi, toi]는 그래프 내에서 fromi에서 toi로의 단방향 간선이 존재함을 나타냅니다.
Return a list answer, where answer[i] is the list of ancestors of the ith node, sorted in ascending order.
answer 배열을 반환하는데, 여기서 answer[i]는 ith 노드의 조상 노드 배열이며, 오름차순으로 정렬되어 있습니다.
A node u is an ancestor of another node v if u can reach v via a set of edges.
u 가 간선 집합에 의해 다른 노드 v 에 도달할 수 있다면 노드 u는 노드 v 의 조상입니다.
Example 1:
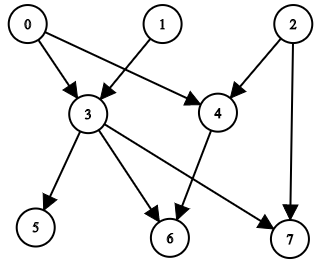
Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.
Example 2:
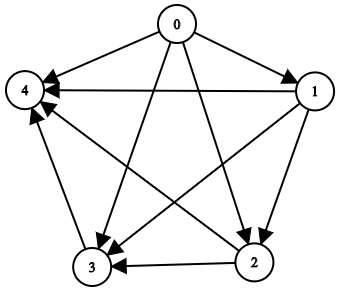
Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Output: [[],[0],[0,1],[0,1,2],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.
Constraints:
1 <= n <= 10000 <= edges.length <= min(2000, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi <= n - 1fromi != toi- There are no duplicate edges.
- The graph is directed and acyclic.
- dfs를 돌며 부모 노드 기록
- 이미 다른 부모노드에 의해 방문되어 기록된 노드에 대해서는 새로운 부모들만 기록하고 dfs 중지
처음에는 위와 같이 생각하고, 코드를 작성했습니다.
처음으로 작성된 코드입니다.
class Solution {
public:
void dfs(vector<vector<int>>& graph, vector<set<int>>& listOfAncestors, set<int>& parents, int currentNode) {
parents.insert(currentNode);
for (int child: graph[currentNode]) {
if (listOfAncestors[child].empty()) {
dfs(graph, listOfAncestors, parents, child);
} else {
for (int i = 0; i < listOfAncestors.size(); i++) {
if (listOfAncestors[i].find(child) != listOfAncestors[i].end()) {
listOfAncestors[i].insert(parents.begin(), parents.end());
}
}
}
listOfAncestors[child].insert(parents.begin(), parents.end());
}
parents.erase(currentNode);
}
vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
vector<vector<int>> graph(n);
for (auto& edge: edges) {
graph[edge[0]].push_back(edge[1]);
}
vector<set<int>> listOfAncestors(n);
for (int i = 0; i < n; i++) {
if (listOfAncestors[i].empty()) {
set<int> parents;
dfs(graph, listOfAncestors, parents, i);
}
}
vector<vector<int>> result(n);
for (int i = 0; i < n; i++) {
result[i] = vector<int>(listOfAncestors[i].begin(), listOfAncestors[i].end());
}
return result;
}
};위 코드를 제출하니 매우 느린 Runtime을 가진다는 것을 알게 되었습니다.
![[Pasted image 20240127164211.png]]
"근본적으로 비효율적인 알고리즘을 생각해냈구나.." 라고 생각하고 여러 가지 최적화를 해보다가, Solution을 참고했습니다.
class Solution {
public:
vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
vector<vector<int>> ans(n), graph(n);
for (auto& e : edges)
graph[e[0]].push_back(e[1]);
for (int i = 0; i < n; i++)
dfs(i, i, ans, graph);
return ans;
}
void dfs(int x, int curr, vector<vector<int>>& ans,
vector<vector<int>>& graph) {
for (auto& ch : graph[curr])
if (ans[ch].size() == 0 || ans[ch].back() != x) {
ans[ch].push_back(x);
dfs(x, ch, ans, graph);
}
}
};위 코드에서 dfs는 다음과 같이 동작합니다.
1. 그래프의 자식 노드에 대해서, 처음 방문했거나 ans[ch](기록된 조상의 맨 뒤 원소)가 x가 아닐 때 ans[ch]의 맨 뒤에 x를 추가해줍니다.
2. dfs를 재귀적으로 호출해줍니다.
그러면 1번 예제에 대해서 아래와 같이 동작하게 됩니다.
dfs(0, 0, ans, directChild)
-> ans[3] = [0]
-> dfs(0, 3, ans, directChild)
-> ans[5] = [0]
-> dfs(0, 5, ans, directChild)
-> 5번의 자식 노드가 없으므로 dfs(0, 5, ans, directChild) 함수 종료
-> dfs(0, 6, ans, directChild)
-> ans[6] = [0]
-> 6번의 자식 노드가 없으므로 dfs(0, 6, ans, directChild) 함수 종료
-> dfs(0, 7, ans, directChild)
-> ans[7] = [0]
-> 7번의 자식 노드가 없으므로 dfs(0, 7, ans, directChild) 함수 종료
-> ans[4] = [0]
-> dfs(0, 4, ans, directChild)
-> ans[6].back == 0 이므로 기록되지 않습니다.
dfs(1, 1, ans, directChild)
-> ans[3] = [1]
-> dfs(1, 3, ans, directChild)
-> ans[5] = [0, 1]
-> dfs(1, 5, ans, directChild)
-> 5번의 자식 노드가 없으므로 dfs(1, 5, ans, directChild) 함수 종료
-> dfs(1, 6, ans, directChild)
-> ans[6] = [0, 1]
-> 6번의 자식 노드가 없으므로 dfs(1, 6, ans, directChild) 함수 종료
-> dfs(1, 7, ans, directChild)
-> ans[7] = [0, 1]
-> 7번의 자식 노드가 없으므로 dfs(1, 7, ans, directChild) 함수 종료
dfs(2, 2, ans, directChild)
-> ans[4] = [0, 2]
-> dfs(2, 4, ans, directChild)
-> ans[6] = [0, 2]
-> dfs(2, 6, ans, directChild)
-> 6번의 자식 노드가 없으므로 dfs(2, 6, ans, directChild) 함수 종료
-> ans[7] = [0, 1, 2]
-> dfs(2, 7, ans, directChild)
-> 7번의 자식 노드가 없으므로 dfs(2, 7, ans, directChild) 함수 종료
dfs(3, 3, ans, directChild)
-> ans[5] = [0, 1, 3]
-> dfs(3, 5, ans, directChild)
-> 5번의 자식 노드가 없으므로 dfs(3, 5, ans, directChild) 함수 종료
-> dfs(3, 6, ans, directChild)
-> ans[6] = [0, 1, 3]
-> 6번의 자식 노드가 없으므로 dfs(3, 6, ans, directChild) 함수 종료
-> dfs(3, 7, ans, directChild)
-> ans[7] = [0, 1, 3]
-> 7번의 자식 노드가 없으므로 dfs(3, 7, ans, directChild) 함수 종료이런 식으로 진행이 되는데, 모든 노드에 대해서 dfs를 돌기는 하지만 vector를 사용해 삽입에 O(1)의 시간이 걸린다는 점과 정렬을 해주지 않아도 된다는 점이 좋아보였습니다.
저의 경우에는 Set 자료형을 사용했기 때문에 삽입/삭제에 O(logN)의 시간이 걸렸고, 이미 방문한 노드를 만났을 경우에는 추가적으로
1. 반복문(O(N))을 돌면서 Set 안에서 child가 있는지 찾고(O(logN)) 원소들을 삽입해주었기 때문에 dfs 안에서도 O(N*logN + logN) = O(N*logN)의 추가적인 시간이 필요했고
2. Set을 Vector로 변환해주는 것이 필요했습니다.
하지만 위의 방법은 모든 노드에 대해서 dfs로 탐색하지만(정확히 말하면 같은 자식 노드를 탐색하지는 않지만) 큰 수정 없이 O(N * (N + E)) 정도의 작은 시간복잡도로 마무리했고, 저는 계산해보니 O(N * (N * (N * logN) + E)) 정도의 끔찍한 시간복잡도를 만들어내었던 것 같습니다.
모든 노드에 대해 dfs를 돌지 않기 위해 다른 방식을 구상했던 것인데 해당 방식이 오히려 제 코드를 더 엉망으로 만들고 있었다는 것이 인상깊습니다..
이런 제 생각이 다른 분들께도 도움이 되었으면 좋겠습니다. 긴 글 읽어주셔서 정말 감사합니다.