2876. Count Visited Nodes in a Directed Graph
Hard
There is a directed graph consisting of n nodes numbered from 0 to n - 1 and n directed edges.
0부터 n-1까지, n개의 방향이 있는 edge로 구성된 방향 그래프가 있다.
You are given a 0-indexed array edges where edges[i] indicates that there is an edge from node i to node edges[i].
index가 0부터 시작하는 배열이 주어지고 각 edges[i]는 node i로부터 node edges[i]로 가게 된다.
Consider the following process on the graph:
그래프에서 다음과 같은 과정을 생각해보자.
-
You start from a node
xand keep visiting other nodes through edges until you reach a node that you have already visited before on this same process. -
노드
x에서 시작해, 이미 방문한 다른 노드를 만날 때까지 edge들을 통해 다른 노드를 계속 방문합니다.
Return an array answer where answer[i] is the number of different nodes that you will visit if you perform the process starting from node i.
node i로부터 시작해 다른 노드를 얼마나 방문할 수 있는지를 answer[i]에 담고 answer 배열을 반환해라.
Example 1:
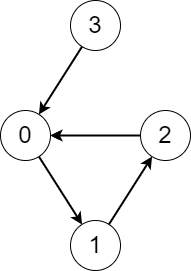
Input: edges = [1,2,0,0]
Output: [3,3,3,4]
Explanation: We perform the process starting from each node in the following way:
- Starting from node 0, we visit the nodes 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 3.
- Starting from node 1, we visit the nodes 1 -> 2 -> 0 -> 1. The number of different nodes we visit is 3.
- Starting from node 2, we visit the nodes 2 -> 0 -> 1 -> 2. The number of different nodes we visit is 3.
- Starting from node 3, we visit the nodes 3 -> 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 4.
Example 2:
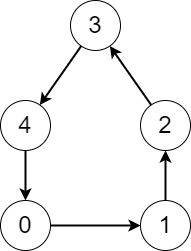
Input: edges = [1,2,3,4,0]
Output: [5,5,5,5,5]
Explanation: Starting from any node we can visit every node in the graph in the process.
Constraints:
n == edges.length2 <= n <= 1050 <= edges[i] <= n - 1edges[i] != i
처음에 아래와 같은 접근 방법을 취했습니다.
- dfs로 그래프를 탐색합니다.
- cycle이 있는 경우, cycle을 돈 후에 cycle의 길이를 해당 node에 기록해줍니다.
- cycle이 없는 곳은 cycle을 만났을 때부터, 거꾸로 +1을 해주며 기록해줍니다.
처음으로 구현한 코드입니다.
class Solution {
public:
vector<int> countVisitedNodes(vector<int>& edges) {
int edgesLength = edges.size();
vector<int> result(edgesLength, -1);
vector<int> currentPath(edgesLength, -1);
for (int i = 0; i < edgesLength; i++) {
if (result[i] != -1) continue;
int nodeIndex = i, length = 0;
fill(currentPath.begin(), currentPath.end(), -1);
while (1) {
currentPath[nodeIndex] = length;
nodeIndex = edges[nodeIndex];
length++;
// cycle을 발견했을 때
if (currentPath[nodeIndex] > -1) {
int cycleLength = length - currentPath[nodeIndex];
currentPath[nodeIndex] = length;
for (int j = 0; j < edgesLength; j++) {
if (currentPath[j] == -1 || result[j] != -1) continue;
if (currentPath[j] >= length - cycleLength) {
result[j] = cycleLength;
} else {
result[j] = length - currentPath[j];
}
}
break;
}
// 이미 지나친 노드를 발견했을 때
if (result[nodeIndex] != -1) {
currentPath[nodeIndex] = length;
for (int j = 0; j < edgesLength; j++) {
if (result[j] != -1 || currentPath[j] == -1) continue;
result[j] = result[nodeIndex] + -(currentPath[j] - length);
}
break;
}
}
}
return result;
}
};-> Time limit exceeded가 발생했습니다.
저는 그 이유를 edgesLength만큼 도는 반복문이 가장 크다고 보고, 해당 부분을 줄여주기 위해서 해당 지나간 노드의 index와 해당 노드를 지나갈 때까지 걸린 length를 같이 기록해주었습니다. tuple 자료형을 이용했습니다.
두 번째 구현된 코드입니다.
class Solution
{
public:
static int isDuplicated(vector<tuple<int, int>> currentPath, int index)
{
if (currentPath.size() == 1)
return -1;
for (const auto &tup : currentPath)
{
int first = std::get<0>(tup);
if (first == index)
return get<1>(tup);
}
return -1;
}
vector<int> countVisitedNodes(vector<int> &edges)
{
int edgesLength = edges.size();
vector<int> result(edgesLength, -1);
vector<tuple<int, int>> currentPath;
for (int i = 0; i < edgesLength; i++)
{
if (result[i] != -1)
continue;
int nodeIndex = i, length = 0;
currentPath.clear();
while (1)
{
currentPath.push_back(make_tuple(nodeIndex, length));
nodeIndex = edges[nodeIndex];
length++;
int duplicatedPathLength = isDuplicated(currentPath, nodeIndex);
if (duplicatedPathLength != -1)
{
int cycleLength = length - duplicatedPathLength;
for (const auto &tup : currentPath)
{
int tupleIndex = get<0>(tup);
int tupleLength = get<1>(tup);
if (tupleLength >= length - cycleLength)
{
result[tupleIndex] = cycleLength;
}
else
{
result[tupleIndex] = length - tupleLength;
}
}
break;
}
if (result[nodeIndex] != -1)
{
for (const auto &tup : currentPath)
{
int tupleIndex = get<0>(tup);
int tupleLength = get<1>(tup);
result[tupleIndex] = result[nodeIndex] + -(tupleLength - length);
}
break;
}
}
}
return result;
}
};tuple을 사용하니 예상치 못한 곳에서 문제가 발생했습니다. 중복이 있는지 탐색하는 곳에서 기존의 O(1)과 다르게 O(N)의 시간 복잡도가 필요로 해졌습니다. 또한, node의 개수가 최대일 때, 기존보다 많은 오버헤드(vector의 크기를 계속해서 늘려주면서 데이터를 복사해주고 옮겨주는 행동이 필요함)가 발생했습니다.
-> 940번째, 10만개 데이터셋에서 Memory Limit Exceeded 발생했습니다.
그 후, tuple을 사용하지 않고 unordered_map을 사용하게 자료구조를 변경해주었습니다.
unordered_map을 사용한, 마지막으로 구현된 코드입니다.
class Solution {
public:
vector<int> countVisitedNodes(vector<int>& edges) {
int edgesLength = edges.size();
vector<int> result(edgesLength, -1);
unordered_map<int, int> visited; // 노드와 깊이를 저장
for (int i = 0; i < edgesLength; i++) {
if (result[i] != -1) continue;
int nodeIndex = i, length = 0;
visited.clear();
while (nodeIndex != -1) {
if (visited.find(nodeIndex) != visited.end()) {
int cycleStart = visited[nodeIndex];
int cycleLength = length - cycleStart;
for (const auto& p : visited) {
if (p.second >= cycleStart) {
result[p.first] = cycleLength;
} else {
result[p.first] = length - p.second;
}
}
break;
}
if (result[nodeIndex] != -1) {
for (const auto& p : visited) {
result[p.first] = result[nodeIndex] + length - p.second;
}
break;
}
visited[nodeIndex] = length;
nodeIndex = edges[nodeIndex];
length++;
}
}
return result;
}
};
푸는데 다른 문제들보다 시간을 많이 썼지만, 그만큼 시간복잡도와 공간복잡도, 자료구조에 대해 많은 생각을 해볼 수 있어서 좋았던 문제였습니다.
한 가지 더 생각해보아야할 점은, 제가 생각한 로직의 시간/공간복잡도가 평균수준이라는 것입니다. 상위권의 시간 복잡도를 가진 코드들을 보았을 때 로직이 크게 다르지 않은 것 같은데 어떤 부분들을 최적화 할 수 있는지 다시 살펴보아야겠습니다.
궁금하신 점이나 여쭈어볼 것이 있으시면 댓글로 남겨주시면 감사하겠습니다.