백준 1005 ACM Craft (Gold 3)

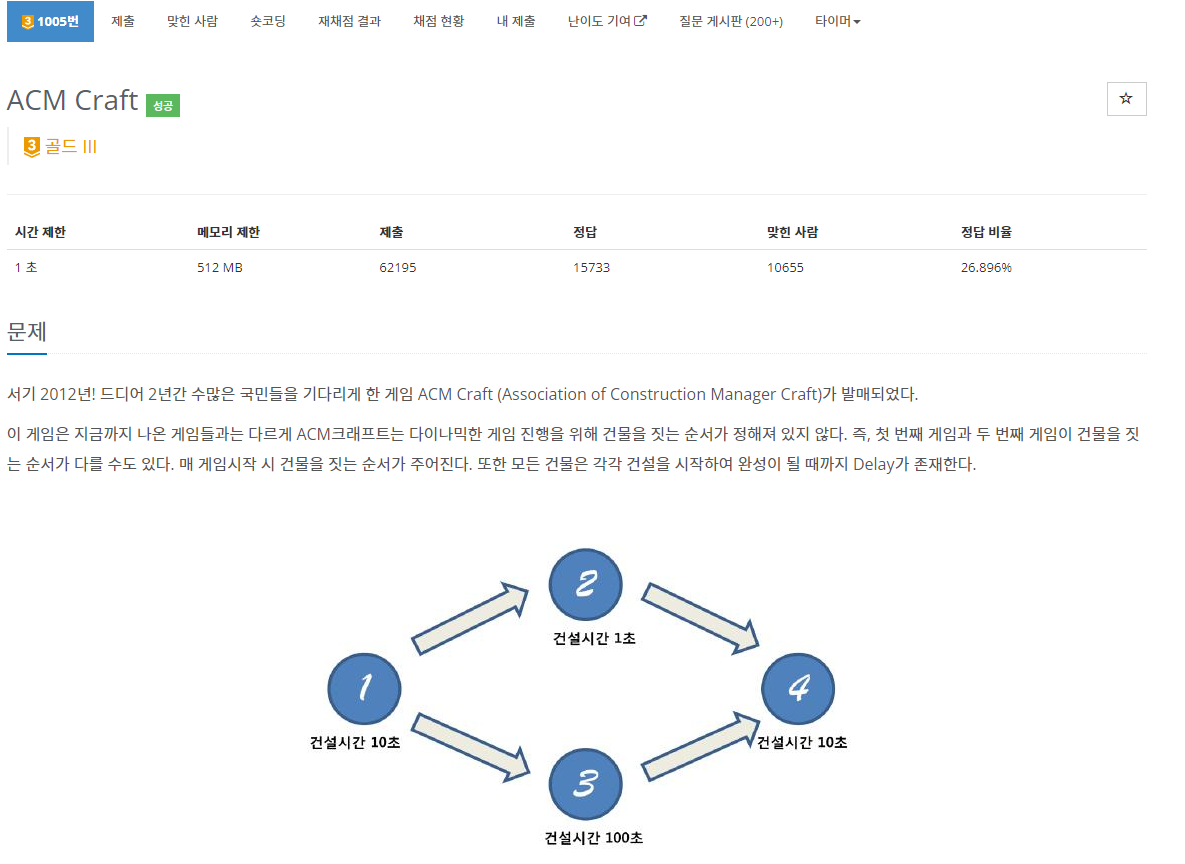
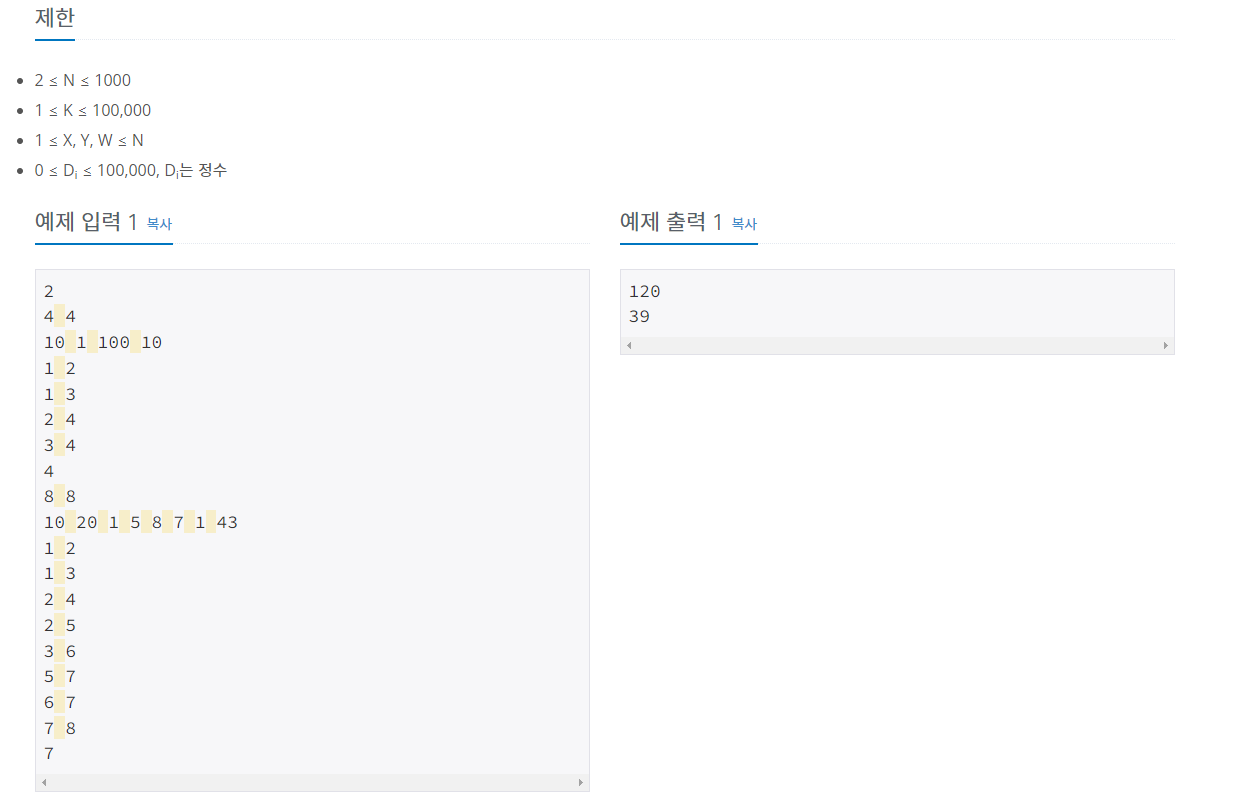
문제 설명

전략

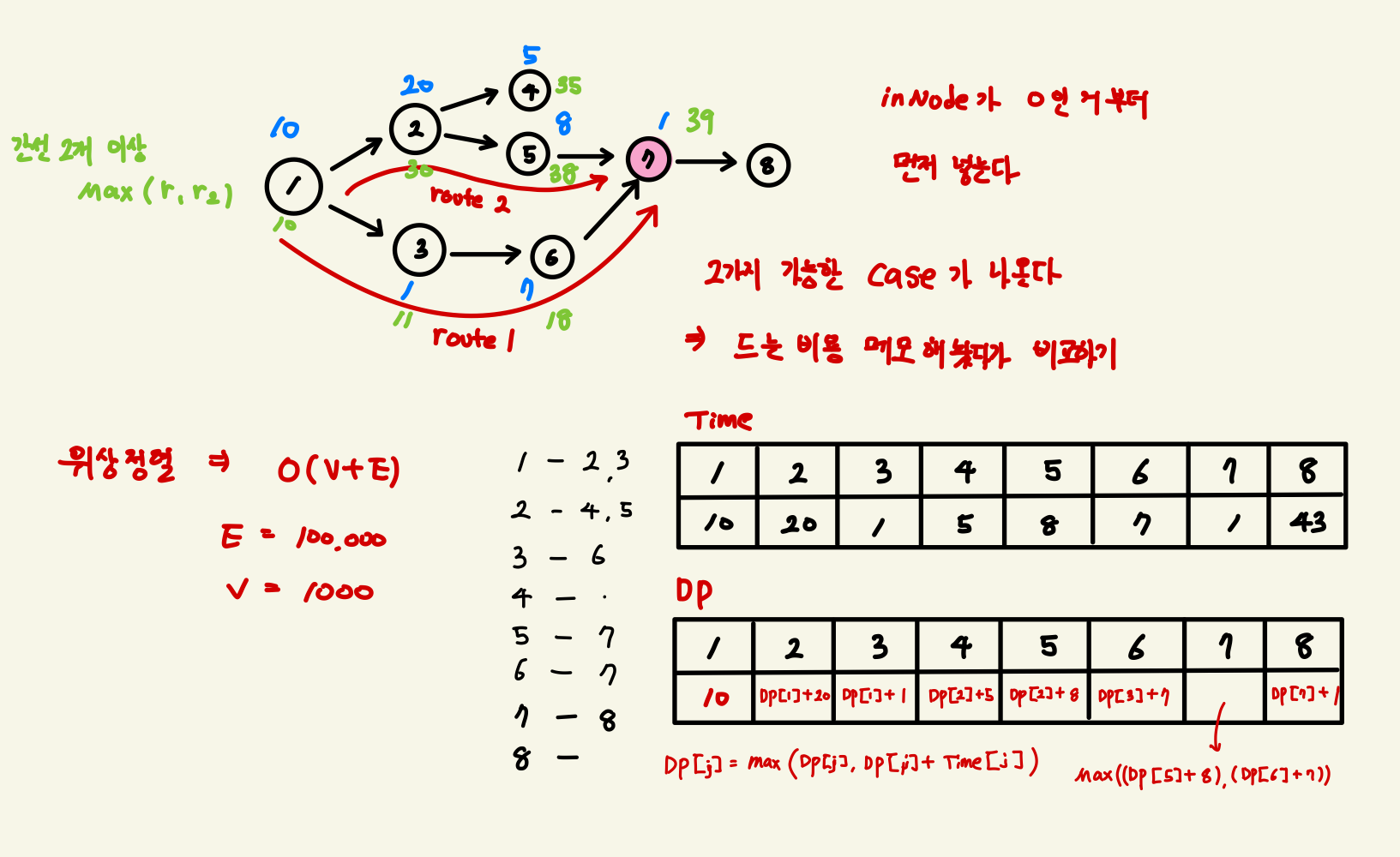
• 문제에서 지어야 하는 건물을 짓기 위해선 이전에 꼭 지어져야 하는 건물이 있다는 것은 위상정렬의 개념으로 접근해야한다

• 위의 그림과 같이 7번 건물을 짓기 위한 그래프를 그려보면 경로가 2개 이상 존재하는 경우가 있다 -> 일반적으로 1개의 경로만 찾으면 되는 위상정렬과는 다름

• 1. 모든 경로를 다 저장해놨다가 비교하는 Brute Force의 방법이 있고
• 2. 이전에 지어야 하는 건물이 지어지는데 걸리는 최대 시간을 계속 저장해나가는 DP적 접근이 가능하다

• 경로의 수가 많아지고 길어진다면 전자의 경우에 저장해야하는 메모리와 시간복잡도가 크게 증가한다. -> DP적 접근이 필요함

정답코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Deque;
import java.util.LinkedList;
import java.util.StringTokenizer;

public class Main {
	static int TC, N, K, W;
	static int[] building; // 각 건물을 짓는데 걸리는 시간
	static int[] dp;
	static int[] inNode;
	static ArrayList<ArrayList<Integer>> Adjacent;
	static StringBuilder sb = new StringBuilder();
	static Deque<Integer> dq;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());

		TC = Integer.parseInt(st.nextToken());

		for (int t = 0; t < TC; t++) {
			st = new StringTokenizer(br.readLine());
			N = Integer.parseInt(st.nextToken());
			K = Integer.parseInt(st.nextToken());
			building = new int[N + 1];
			dp = new int[N + 1];
			inNode = new int[N + 1];
			dq = new LinkedList<>();

			st = new StringTokenizer(br.readLine());

			// 건물 짓는 시간 초기화
			for (int i = 1; i < N + 1; i++) {
				building[i] = Integer.parseInt(st.nextToken());
			}

			// 인접 리스트 초기화
			Adjacent = new ArrayList<ArrayList<Integer>>();
			for (int i = 0; i < N + 1; i++) {
				Adjacent.add(new ArrayList<Integer>());
			}

			for (int i = 0; i < K; i++) {
				st = new StringTokenizer(br.readLine());
				int start = Integer.parseInt(st.nextToken());
				int end = Integer.parseInt(st.nextToken());

				Adjacent.get(start).add(end);

				// 들어오는 간선 추가
				inNode[end]++;
			}

			st = new StringTokenizer(br.readLine());
			W = Integer.parseInt(st.nextToken());
			
			
			for (int i = 1; i < N + 1; i++) {
				// 들어오는 간선이 없을 때
				if (inNode[i] == 0) {
					//위상정렬 queue에 넣어주고 
					dq.add(i);
					//초기 dp값은 자기 자신번호 건물을 짓는 시간
					dp[i] = building[i]; 
				}
			}
				
			while (!dq.isEmpty()) {				
				int now = dq.poll();
				for (int i = 0; i < Adjacent.get(now).size(); i++) {
					int nextNode = Adjacent.get(now).get(i);
					//현재 건물을 짓기 위해서 자신과 이전에 가장 늦게지어지는 건물 + 자기 건설시간을 비교해서 최댓값
					dp[nextNode] = Math.max(dp[nextNode], dp[now]+building[nextNode]);
					inNode[nextNode]--;
					if(inNode[nextNode]==0)dq.add(nextNode);
				}
			}
			
			sb.append(dp[W]).append('\n');
		}
		System.out.println(sb);
	}
}