프로그래머스 Lv.2 미로 탈출

문제설명

1 x 1 크기의 칸들로 이루어진 직사각형 격자 형태의 미로에서 탈출하려고 합니다. 각 칸은 통로 또는 벽으로 구성되어 있으며, 벽으로 된 칸은 지나갈 수 없고 통로로 된 칸으로만 이동할 수 있습니다.

통로들 중 한 칸에는 미로를 빠져나가는 문이 있는데, 이 문은 레버를 당겨서만 열 수 있습니다. 레버 또한 통로들 중 한 칸에 있습니다.

따라서, 출발 지점에서 먼저 레버가 있는 칸으로 이동하여 레버를 당긴 후 미로를 빠져나가는 문이 있는 칸으로 이동하면 됩니다. 이때 아직 레버를 당기지 않았더라도 출구가 있는 칸을 지나갈 수 있습니다. 미로에서 한 칸을 이동하는데 1초가 걸린다고 할 때, 최대한 빠르게 미로를 빠져나가는데 걸리는 시간을 구하려 합니다.

미로를 나타낸 문자열 배열 maps가 매개변수로 주어질 때, 미로를 탈출하는데 필요한 최소 시간을 return 하는 solution 함수를 완성해주세요. 만약, 탈출할 수 없다면 -1을 return 해주세요.

제한사항

• 5 ≤ maps의 길이 ≤ 100, 5 ≤ maps[i]의 길이 ≤ 100
  
  
• maps[i]는 다음 5개의 문자들로만 이루어져 있습니다.
  S : 시작 지점
  E : 출구
  L : 레버
  O : 통로
  X : 벽
  
  
• 시작 지점과 출구, 레버는 항상 다른 곳에 존재하며 한 개씩만 존재합니다.
  출구는 레버가 당겨지지 않아도 지나갈 수 있으며, 모든 통로, 출구, 레버, 시작점은 여러 번 지나갈 수 있습니다.

입출력 예

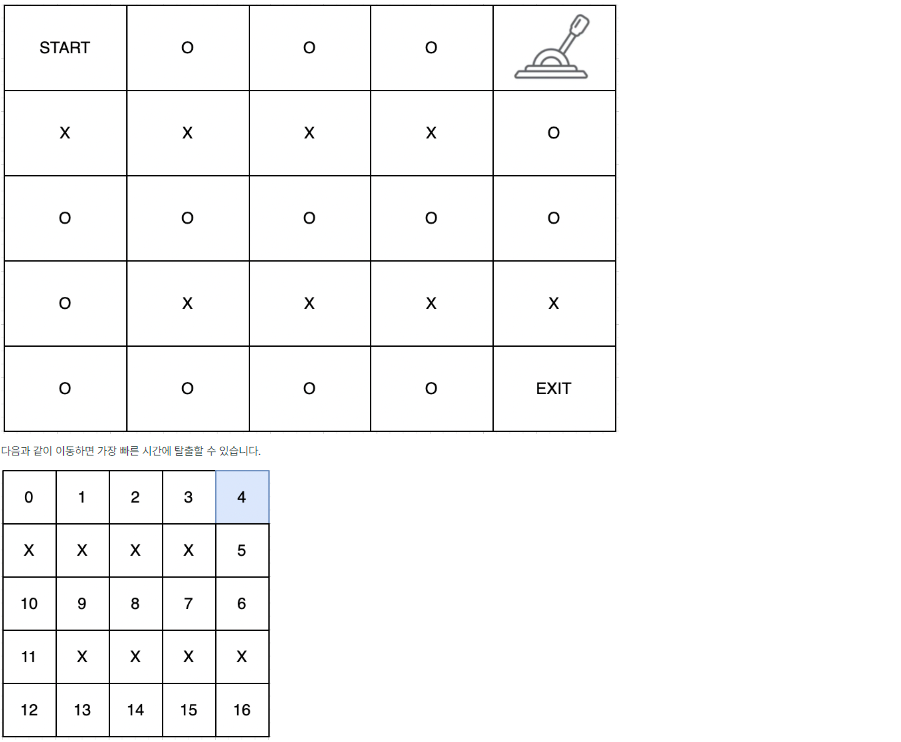
정답코드

import java.util.Queue;
import java.util.LinkedList;

class Node{
    
    int x;
    int y;
    int depth;
    
    Node(int x, int y, int depth){
        this.x = x;
        this.y = y;
        this.depth = depth;
    }
}


class Solution {
    static char [][] map;
    static int N = 0;
    static int M = 0;
    static int startX = 0;
    static int startY = 0;
    static int leverX = 0;
    static int leverY = 0;
    static int endX = 0;
    static int endY = 0;
    static int answer = 0; 
    static int [] dx = {-1,1,0,0};
    static int [] dy = {0,0,-1,1};
    
    public int solution(String[] maps) {
        
        N = maps.length;
        M = maps[0].length();
        
        map = new char[N][M]; 
        
        for(int i = 0; i < N; i++){
            String input = maps[i];
            for(int j = 0; j < M; j++){
                map[i][j] = input.charAt(j);
                if(input.charAt(j) == 'S'){
                    startX = i;
                    startY = j;
                }
                else if(input.charAt(j) == 'L'){
                    leverX = i;
                    leverY = j;
                }
                else if(input.charAt(j) == 'E'){
                    endX = i;
                    endY = j;
                }
            }
        }
        
        int StoL = bfs(startX,startY,'L');
        if(StoL == -1)return -1;
        answer+=StoL;
        
        int LtoE = bfs(leverX,leverY,'E');
        
        if(LtoE == -1)return -1;
        else{
            System.out.println(LtoE);
            return answer+=LtoE;
        }

    }
    
    public static int bfs(int Bx, int By,  char c){
        
        Queue<Node>queue = new LinkedList<>();
        Node nd = new Node(Bx,By,0);
        queue.offer(nd);
        boolean [][] visited = new boolean[N][M];
        visited[Bx][By] = true;
        
        
        while(!queue.isEmpty()){ 
            Node nowNode = queue.poll();
            int x = nowNode.x;
            int y = nowNode.y;
            int depth = nowNode.depth;
            if(map[x][y] == c)return nowNode.depth;
            
            for(int i = 0; i < 4; i++){
                int nx = x+dx[i];
                int ny = y+dy[i];
                
                if(nx<0||ny<0||nx>=N||ny>=M||map[nx][ny]=='X'||visited[nx][ny])continue;
                
                Node newNode = new Node(nx,ny,depth+1);
                queue.offer(newNode);
                visited[nx][ny] = true;
            }
        }
        
        return -1;
    }
}

피드백

최단거리 문제는 BFS를 이용하는데 굳이 Depth별로 할 필요가 없다면 일반적인 버전으로 풀자, 그리고 distance를 직접 안 새고 visited에 한번에 처리해서 visited[nx][ny] = visited[x][y]+1 식으로도 가능 걸린시간 40분, 난이도 : 4/10