프로그래머스 Lv.2 요격 시스템

문제 설명

A 나라가 B 나라를 침공하였습니다. B 나라의 대부분의 전략 자원은 아이기스 군사 기지에 집중되어 있기 때문에 A 나라는 B 나라의 아이기스 군사 기지에 융단폭격을 가했습니다.

A 나라의 공격에 대항하여 아이기스 군사 기지에서는 무수히 쏟아지는 폭격 미사일들을 요격하려고 합니다. 이곳에는 백발백중을 자랑하는 요격 시스템이 있지만 운용 비용이 상당하기 때문에 미사일을 최소로 사용해서 모든 폭격 미사일을 요격하려 합니다.

A 나라와 B 나라가 싸우고 있는 이 세계는 2 차원 공간으로 이루어져 있습니다. A 나라가 발사한 폭격 미사일은 x 축에 평행한 직선 형태의 모양이며 개구간을 나타내는 정수 쌍 (s, e) 형태로 표현됩니다. B 나라는 특정 x 좌표에서 y 축에 수평이 되도록 미사일을 발사하며, 발사된 미사일은 해당 x 좌표에 걸쳐있는 모든 폭격 미사일을 관통하여 한 번에 요격할 수 있습니다. 단, 개구간 (s, e)로 표현되는 폭격 미사일은 s와 e에서 발사하는 요격 미사일로는 요격할 수 없습니다. 요격 미사일은 실수인 x 좌표에서도 발사할 수 있습니다.

각 폭격 미사일의 x 좌표 범위 목록 targets이 매개변수로 주어질 때, 모든 폭격 미사일을 요격하기 위해 필요한 요격 미사일 수의 최솟값을 return 하도록 solution 함수를 완성해 주세요.

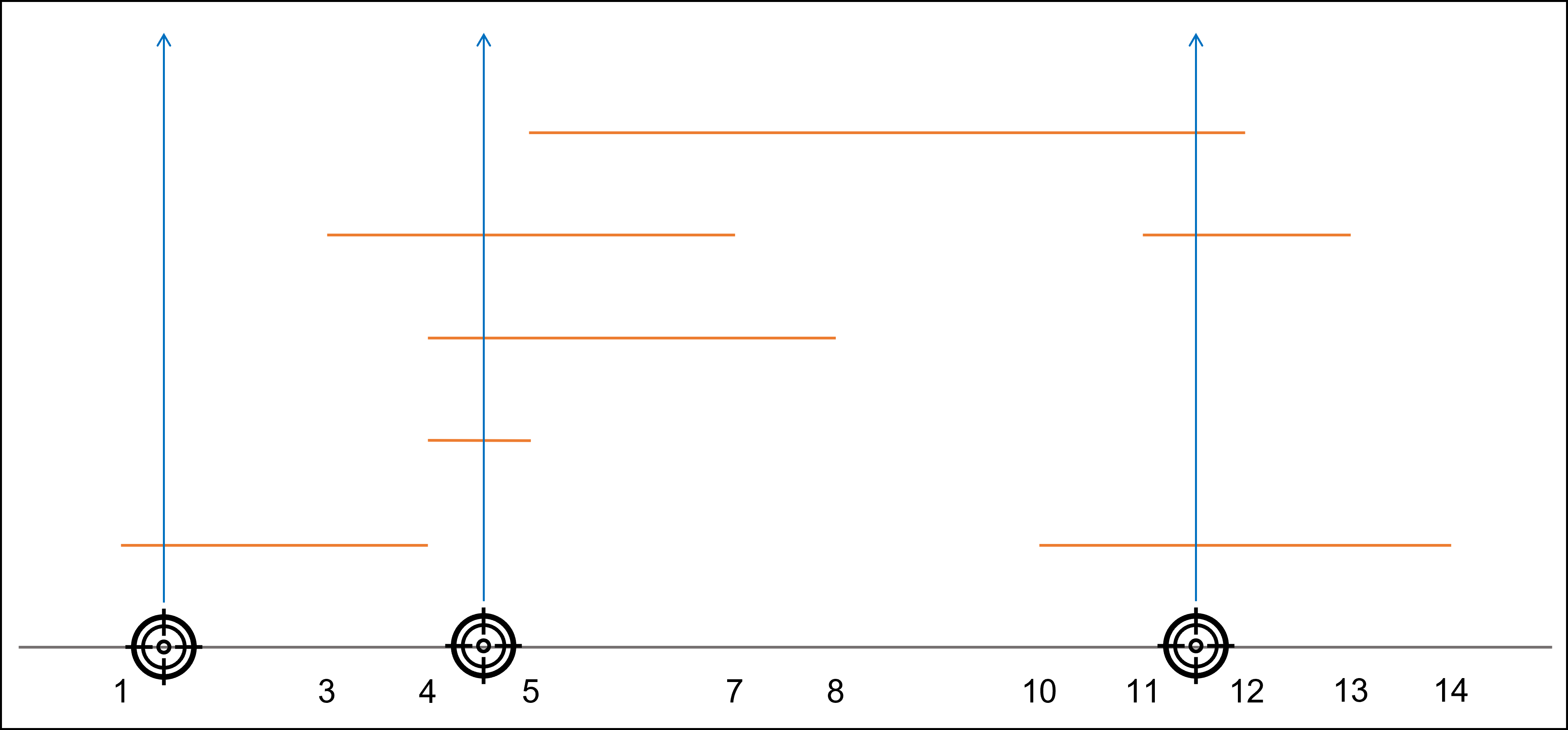
제한 사항

1 ≤ targets의 길이 ≤ 500,000
targets의 각 행은 [s,e] 형태입니다.
이는 한 폭격 미사일의 x 좌표 범위를 나타내며, 개구간 (s, e)에서 요격해야 합니다.
0 ≤ s < e ≤ 100,000,000

입출력 예

정답코드

import java.util.*;

class missile implements Comparable<missile> {
    int start;
    int end; 
    
    public missile(int start, int end){
        this.start = start;
        this.end = end;
    }
    
    public int compareTo(missile m){
        if(this.start != m.start)return this.start - m.start;
        return this.end - m.end;
    }
    
}


class Solution {
    public int solution(int[][] targets) {
        int answer = 0;
        
        PriorityQueue<missile>pq = new PriorityQueue<>();
        
        //시작 순서가 빠른 순으로, 같다면 끝나는 지점이 빠른 순으로
        for(int i = 0; i < targets.length; i++){
            missile m = new missile(targets[i][0],targets[i][1]);
            pq.add(m);
        }
        
        
        int end = -1; 
        
        while(!pq.isEmpty()){
            missile m = pq.poll(); 
            
            //다음 미사일의 시작 지점이 앞의 끝 지점을 넘는다면 새로운 미사일로 요격해야한다
            if(m.start >= end){
                answer++;
                end = m.end;
                continue;
            }
            
            //미사일 길이의 끝이 짧은 걸로 업데이트 이전 미사일로 요격은 가능 but 끝지점이 줄어든다
            if(m.end < end){
                end = m.end;
            }
            
        }
        
        return answer;
    }
}

백준에 회의실 배정문제와 비슷한 그리디 문제. 딱 보자마자 그리디 인 것을 눈치채야한다. 전형적인 유형이긴 함 난이도 6/10 걸린시간 1시간 10분