Deadline Scheduling

Deadline Scheduling

• 문제 정의
  • N개의 일들이 있다. $J_{1}, J_{2},, ... J_{n}$으로 정의한다.
  • 각각의 일 $J_{i} = (D_{i}, P_{i})$
    • $D_{i}$ = 적어도 일이 들어가야 하는 시간(Deadline)
    • $P_{i}$ = 이득(Profit)
  • 일을 넣을 수 있는 슬롯이 있다.
  • 각각의 슬롯은 하나의 일만 들어갈 수 있다.
  • 가장 최고의 이득을 얻으려면 어떻게 배열해야 하는가?
• 예시 : ${(2,2), (1,3), (1,1)}$
  • $\square\square\square\square\square$
  • 1번 슬롯에는 $(1,3),(1,1), (2,2)$이 들어갈 수 있고 2번 슬롯에는 $(2,2)$ 하나만 들어갈 수 있다. 이 경우 1번 슬롯에 $(1,3)$을 넣고, 2번 슬롯에 $(2,2)$를 넣는 경우가 최고의 이득이다.

가정

• 슬롯의 개수는 N보다 작다.(deadlines≤N)
  • 슬롯의 개수가 N보다 커봤자 쓸모가 없음. 어차피 일이 없기 때문에...
• 일들은 이득이 줄어드는 형태(nonincreasing)로 정렬된다.
  • 문제 풀이를 쉽게 하기 위해서 앞에서부터 Profit이 높은 순으로 정렬한다.
• 자신의 Deadline 뒤쪽에 일이 나오는 경우가 없다.
  • Deadline 뒤쪽의 일이 나온다는 말은 일이 들어가야 하는 시간을 지난 것과 동일함. 다시 말해 이득이 0인 것과 마찬가지임.

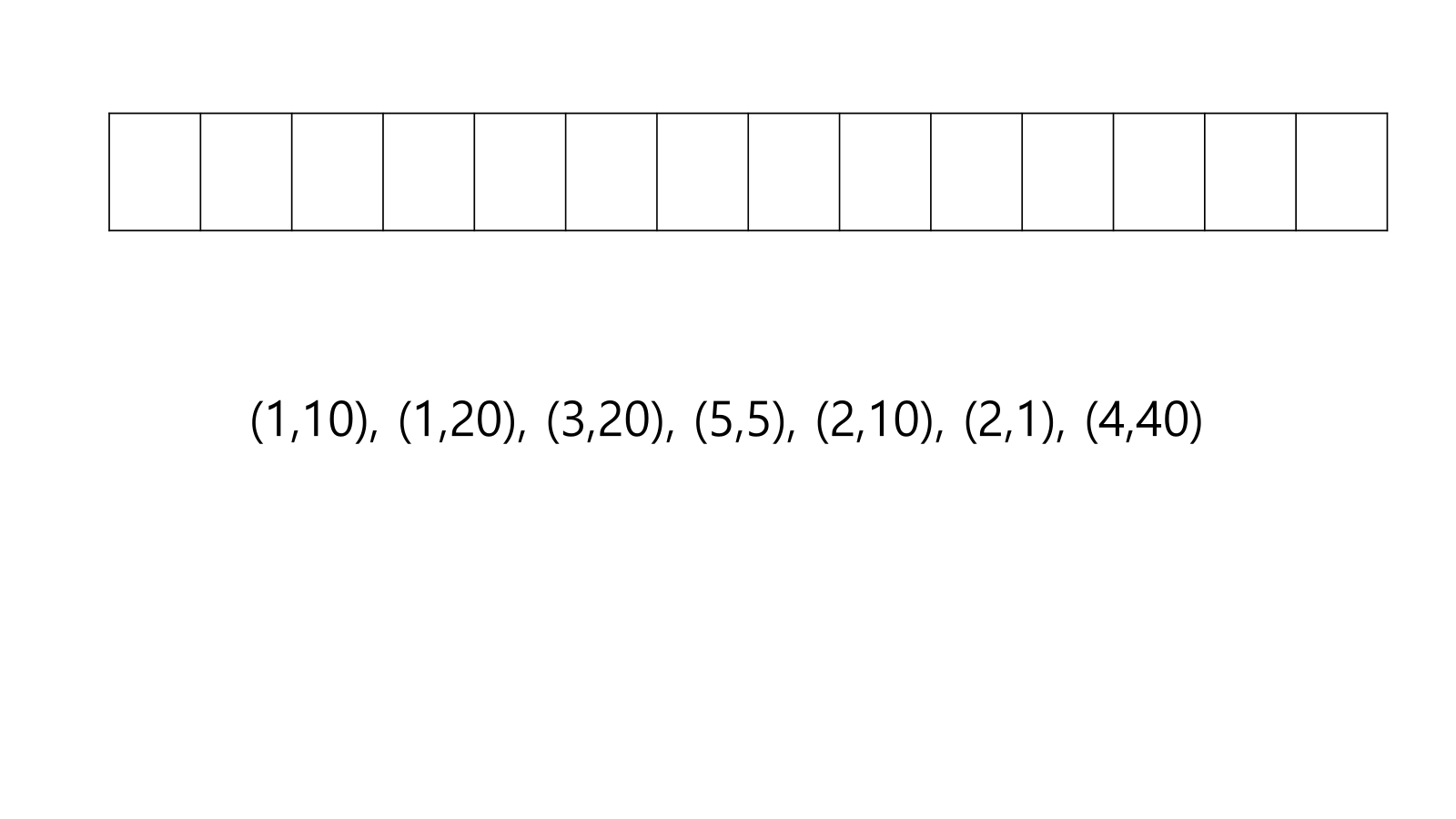
Intuition/Algorithm

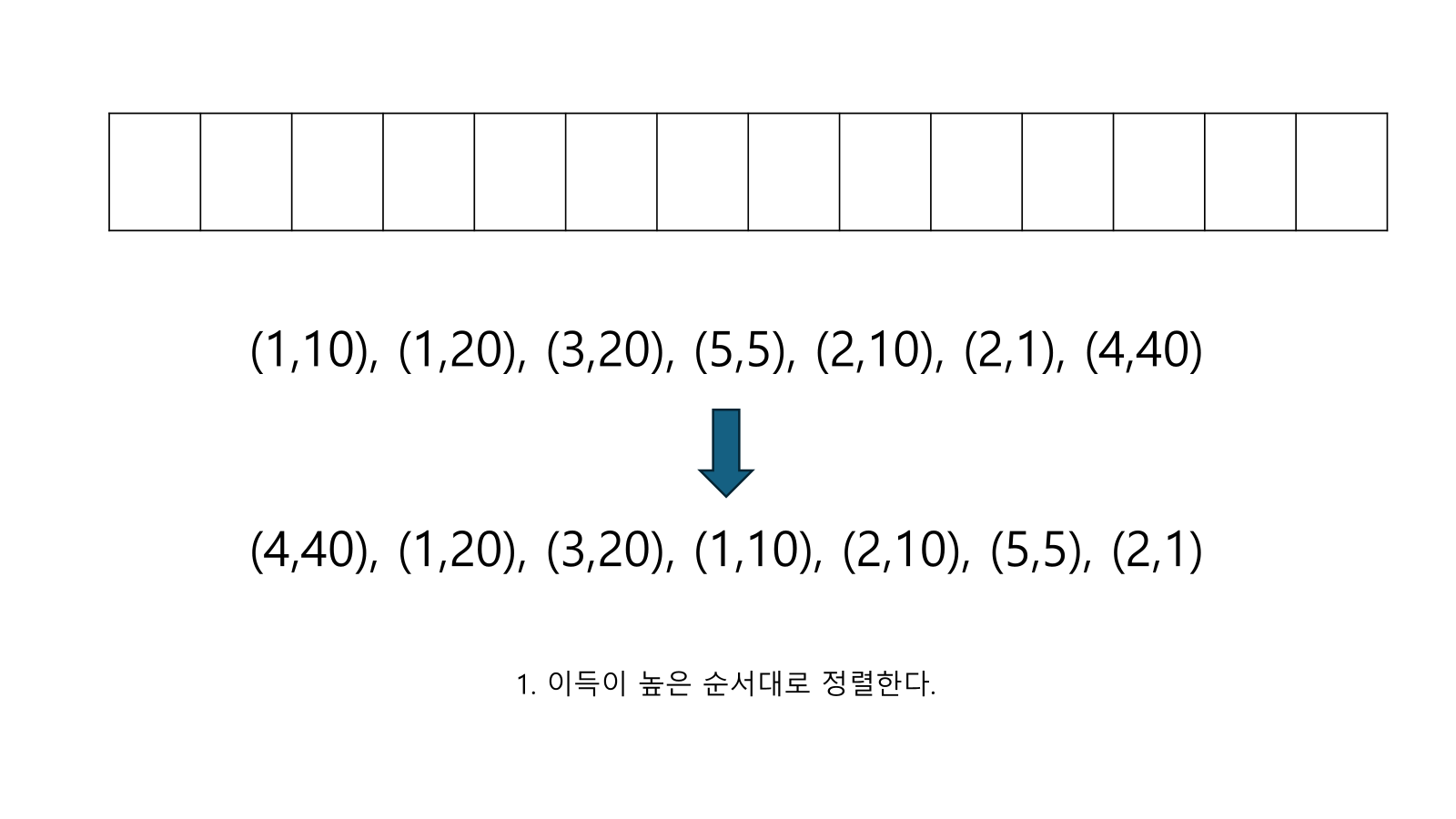
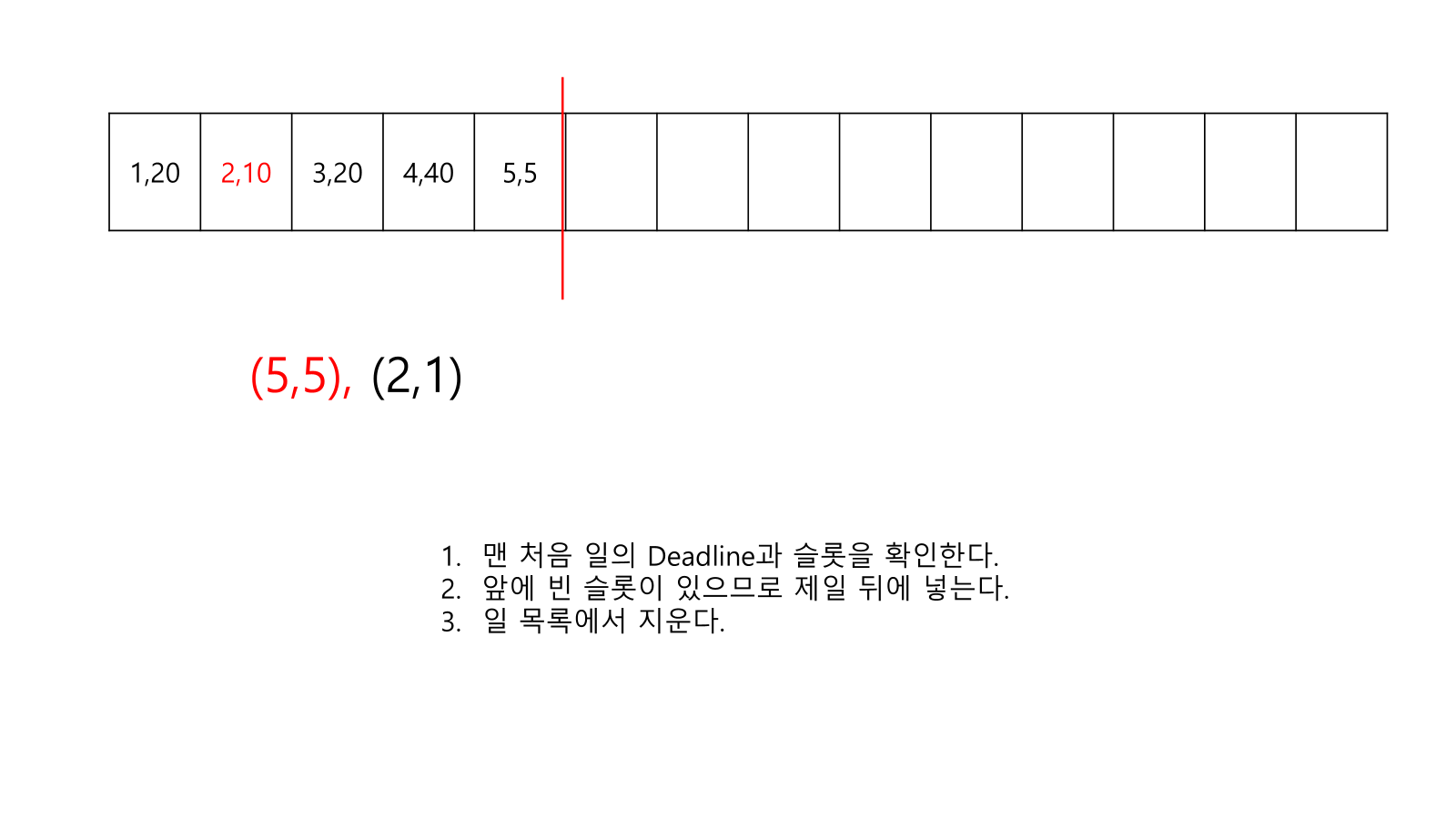
• 이득이 높은 순서대로 넣는다. 이를 위해서 정렬을 한다.
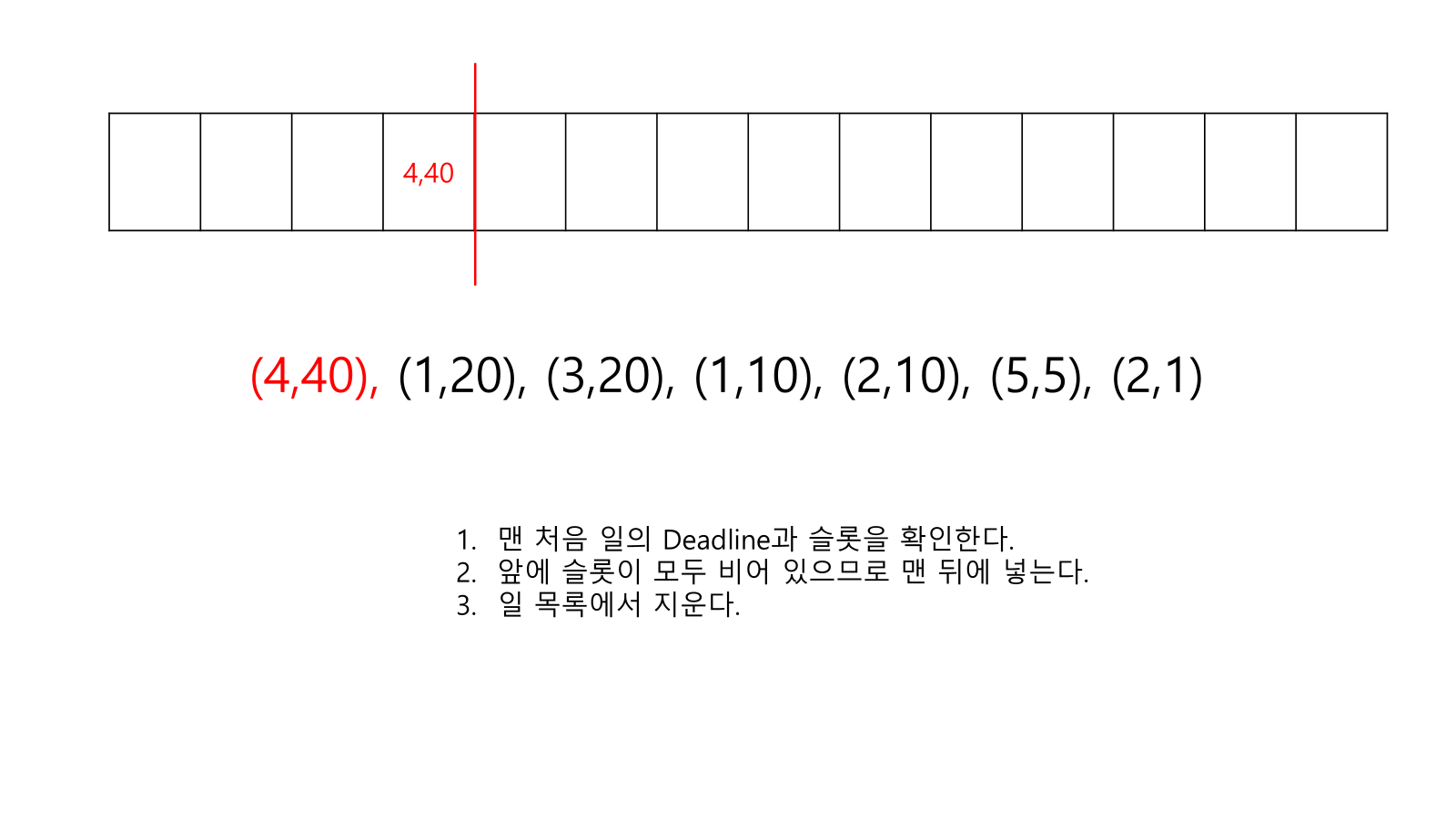
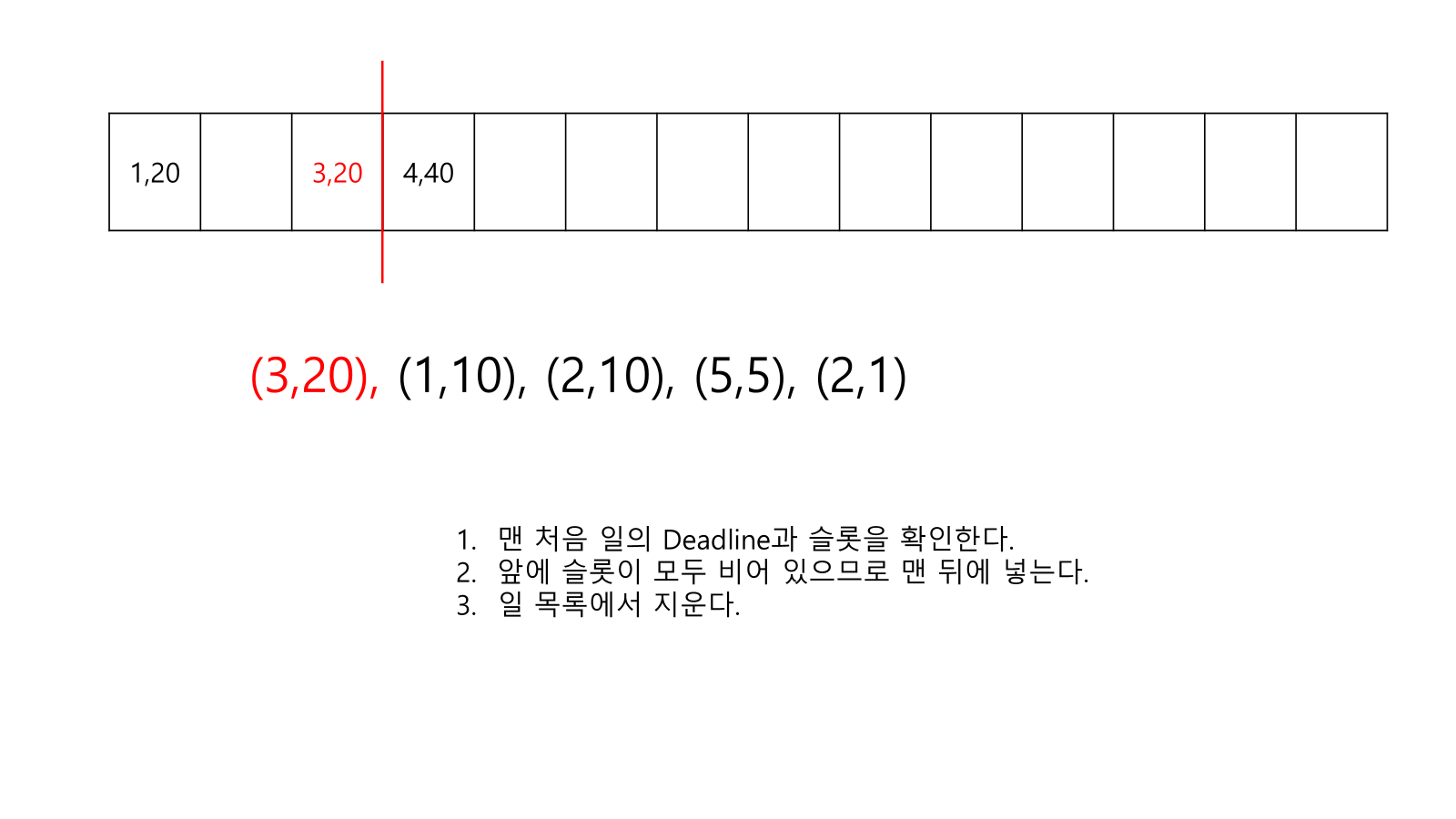
• 빈 슬롯이 여러개가 있으면 최대한 뒤쪽에 넣는다.
  
  
  
  
  
  
  
  
  

Correctness

• 이 알고리즘을 따르는 슬롯을 $A$, 정답을 $S$라고 부르자.
• Invariant : $J_{i}$까지 본 후, 알고리즘 $A$가 정답 $S$가 같은지 확인한다.
  • j ≤ i일때, $J_{i}$가 $A$에 있으면 $S$에도 있어야하며 반대도 동일하다.
  • 더 나아가, $J_{i}$는 $A$와 $S$의 동일한 위치에 있어야 한다.

Proof of Invariant

• Base) $i=0$이면 공허참이다.
• Step) $i$번째에 Invariant가 참이면 $i+1$번째에도 참이다.
• Step은 두가지 case로 나뉜다.
  • $J_{i+1}$을 $A$에 추가하지 않음.
  • $J_{i+1}$을 $A$에 추가함

$J_{i+1}$을 $A$에 추가하지 않음.

• $J_{i+1}$가 $A$에 추가되지 않는다는 말은 $J_{i+1} = (D_{i+1}, P_{i+1})$에서 $A$의 $D_{i+1}$ 앞에 있는 슬롯들은 모두 다른 $J$로 차있다는 뜻임.
• invariant에 따라 이전의 $A$와 $S는$ 같으므로, $S$의 $D_{i+1}$ 앞에 있는 슬롯들은 모두 다른 $J$로 차 있음.
• 그러므로 $J_{i+1}$가 $S$에 나오려면 Deadline의 뒤에 나올 수 밖에 없고, 이는 불가능 하므로 $S$에 $J_{i+1}$는 추가되지 않음.
• 그러므로 invarient가 여전히 성립함
  

$J_{i+1}$을 $A$에 추가함

먼저, $J_{i+1}$을 $A$에 추가했다는 소리는 $J_{i+1} = (D_{i+1}, P_{i+1})$에서 $A$의 $D_{i+1}$ 앞에 있는 슬롯들 중 하나 이상이 비어있었다는 소리임.
여기서 $J_{i+1}$를 $X$ 번째 자리에 배치했다고 가정함.

• S안에 $J_{i+1}$이 없으면
  • S의 $X$번째 자리가 비어있다 : S가 정답인 것에 모순됨. 왜냐하면 S는 최적화된 값을 내놓아야 하는데, 이렇게 되면 A가 S보다 좋은 결과를 만들어내므로 S의 X번째 자리는 비어있을 수 없음.
  • S의 $X$번째 자리가 다른 $J$로 차있다 : 이 알고리즘에서 profit은 높은 순서대로 나오므로 S의 $X$번째 자리는 더 좋은 $J_{i+1}$로 바뀌게 됨.
    
• S안에 $J_{i+1}$이 있으면
  • S의 $X$번째 자리는 $J_{i+1}$이다. : A=S를 자동으로 만족함.
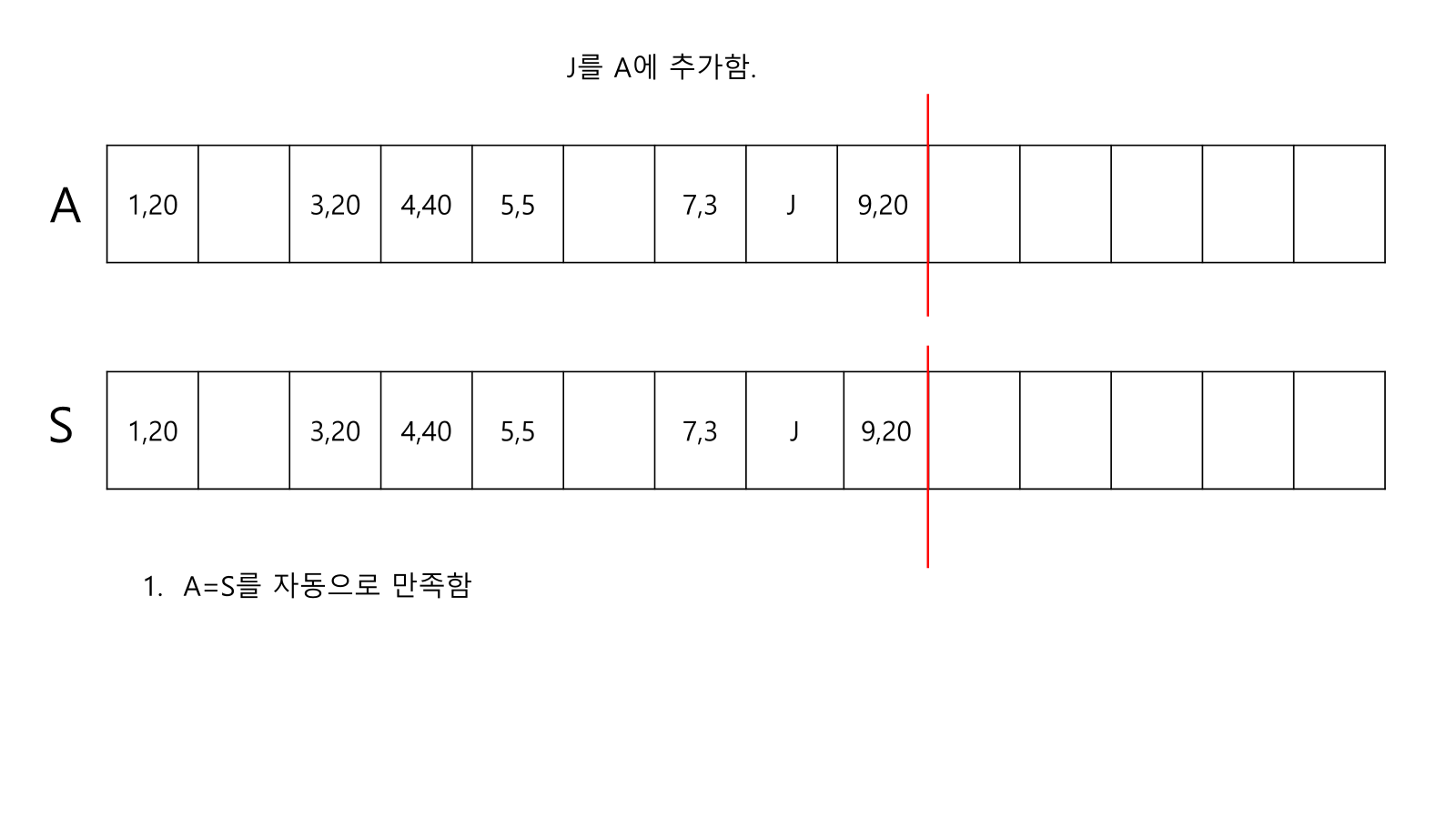
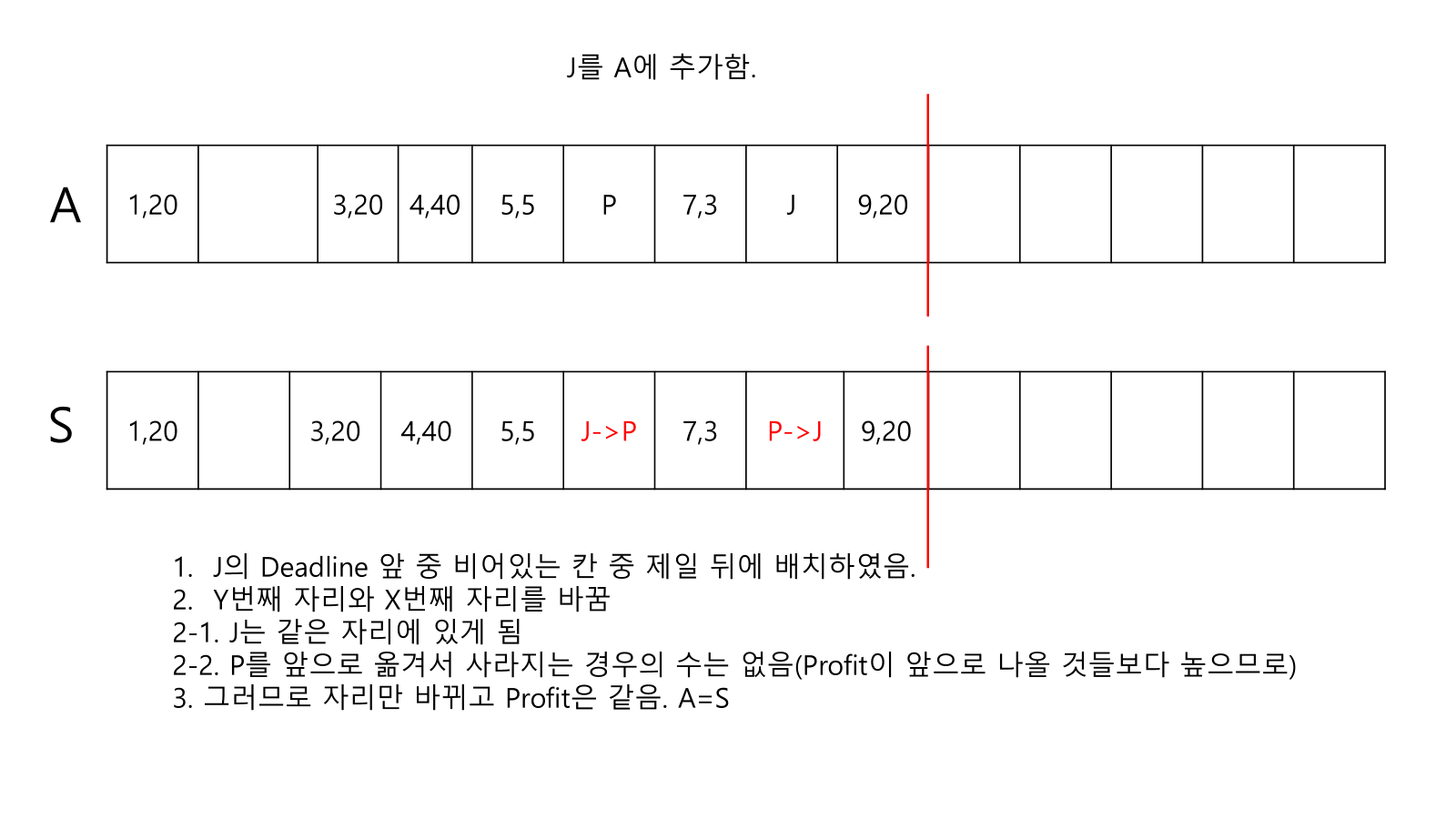
  • $Y < X$일 때, S의 $Y$번째 자리는 $J_{i+1}$이다. : X와 Y의 일을 바꾼다. 자리만 바뀌고 Profit은 동일하므로 A=S임.
    
  • $Y > X$일 때, S의 $Y$번째 자리는 $J_{i+1}$이다. : 이 경우 $X$와 $Y$사이는 꽉 차있다. 그러면 $Y$는 Deadline을 벗어나게 되므로 불가능함.

성능

• 그냥 알고리즘을 따라가면 $O(N^2)$가 나오게 된다.
• Balanced Tree를 사용하면 성능을 올릴 수 있다.
  • 모든 슬롯에 Deadline에 따라서 일을 넣고 정렬한다.
  • 살아있는 칸들 중 $D_{i}$ 이하에 있는 일 중 제일 큰 $D_{i}$를 찾아서 넣는다. 만약 같다면 값이 큰 것을 넣는다.
  • $O(NlogN)$