Shotest Path

Shotest Path

Shortest Path(최단 경로)는 가중치가 있는 그래프에서 어떤 정점에서 다른 정점으로 이동하기까지 가장 짧은 가중치의 합으로 목적지에 도달하는 방법을 찾기 위한 전략이다.

Dijkstra Algorithm

Algorithm Dijkstra(G, n, v0, Dmin)
- For u ∈ V do Dmin(u) <- g(v0, u)
- R <- {v0} //Dmin(v) is Red for Red Nodes
- While |R| < n do
  - Among nodes not in R, find u with smallest dmin(u)
  - R <- R ∪ {u}
  - For w not ∈ R do Dmin(w) <- min[Dmin(w), Dmin(u) + g(u,w)]
  - //Dmin(w) is Blue for Blue Nodes

Red Node / Blue Node

$R$(Red Node) : Shortest Path가 존재하는 노드
$B$(Blue Node) : Red Node의 인접 노드

$R$에 추가하는 노드는 $B$중 Path가 제일 작은 노드이다.

• $R$는 이미 정답이 나와있는 노드이다.
• $B$중 지금까지의 Path가 제일 작은 것을 $B_s$라고 하자.
  • $B_s$까지 가는 Path가 Shortest Path가 아니라고 해보자.
  • 이 말은 다른 Blue Node인 임의의 $B_i$를 거쳐서 $B_s$로 가야 한다는 의미이다.
  • 그러나 다른 $B_i$를 거치는 순간 Path는 늘어난다. 왜냐하면 $B_s$는 Path가 제일 작기 때문이다.
  • 그러므로 $B_s$까지 가는 Path는 Shortest Path이다.
• $B_s$를 $R$에 추가한다.
• Shortest Path를 갱신한다.
• 반복한다.

$B$를 우선순위 큐로 구현한다. 이 때 우선순위 큐에 A에서 B로 간다는 메세지를 넣는다. 갱신을 편하게 하기 위해서이다.

Example

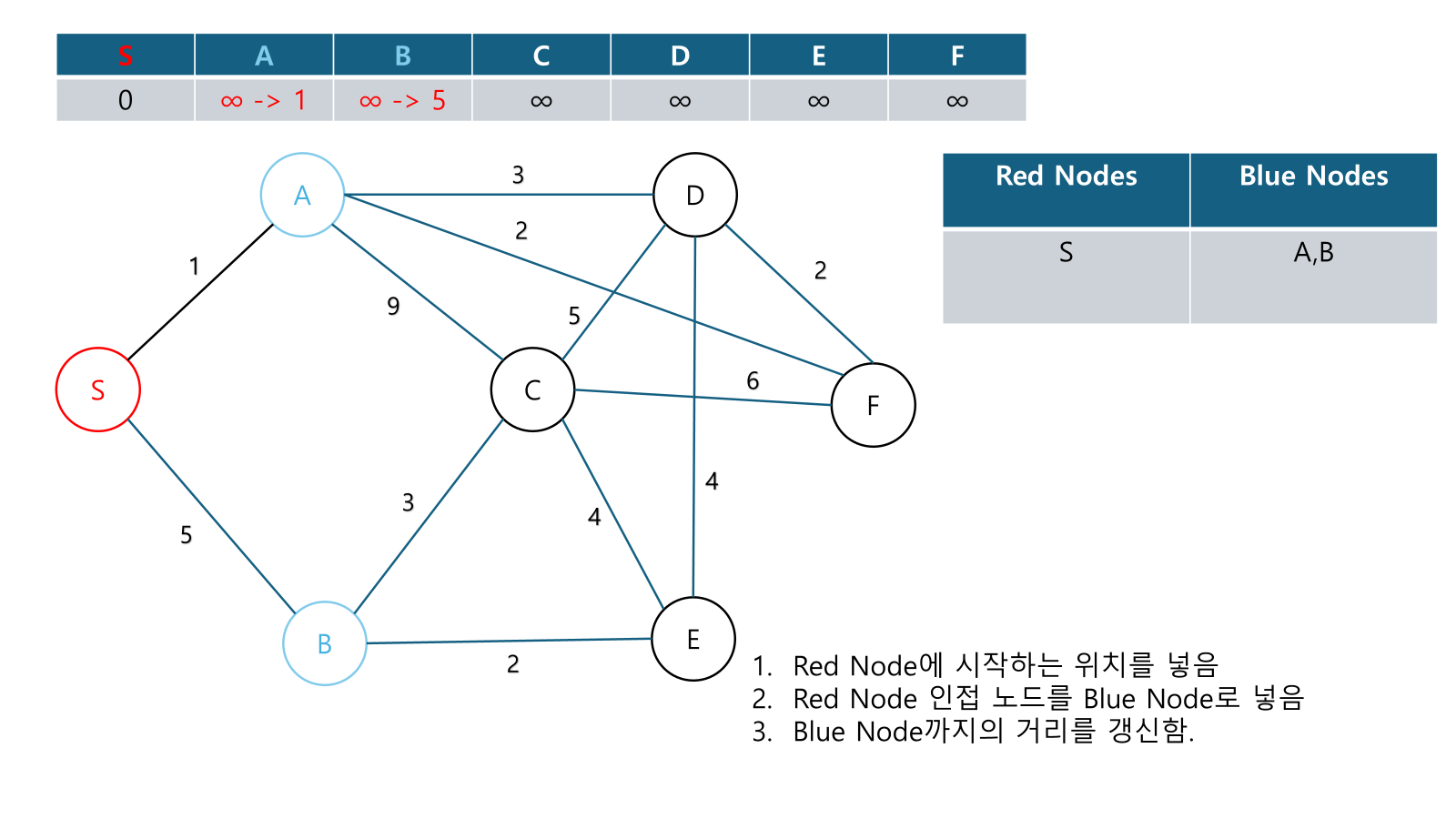
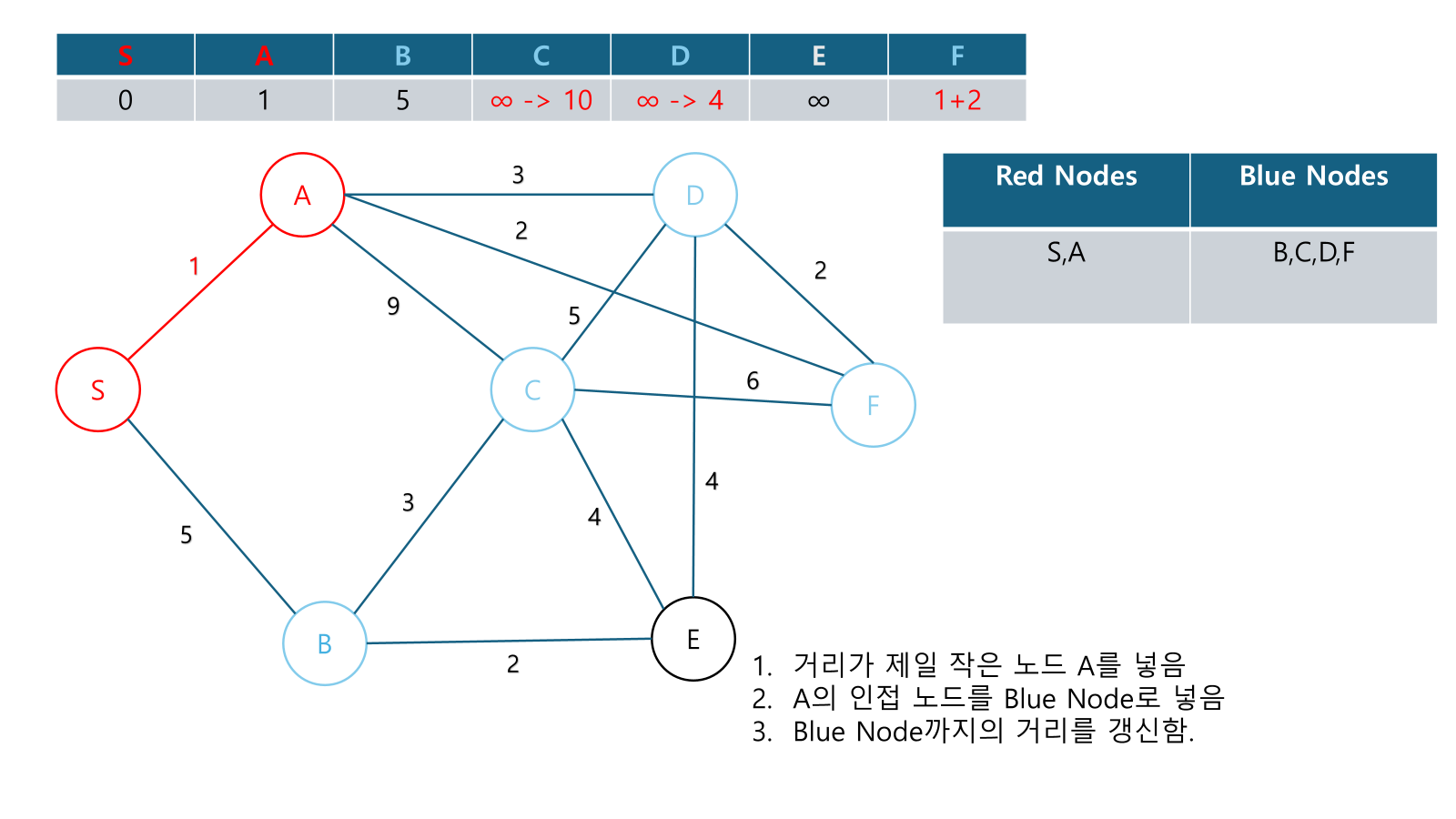
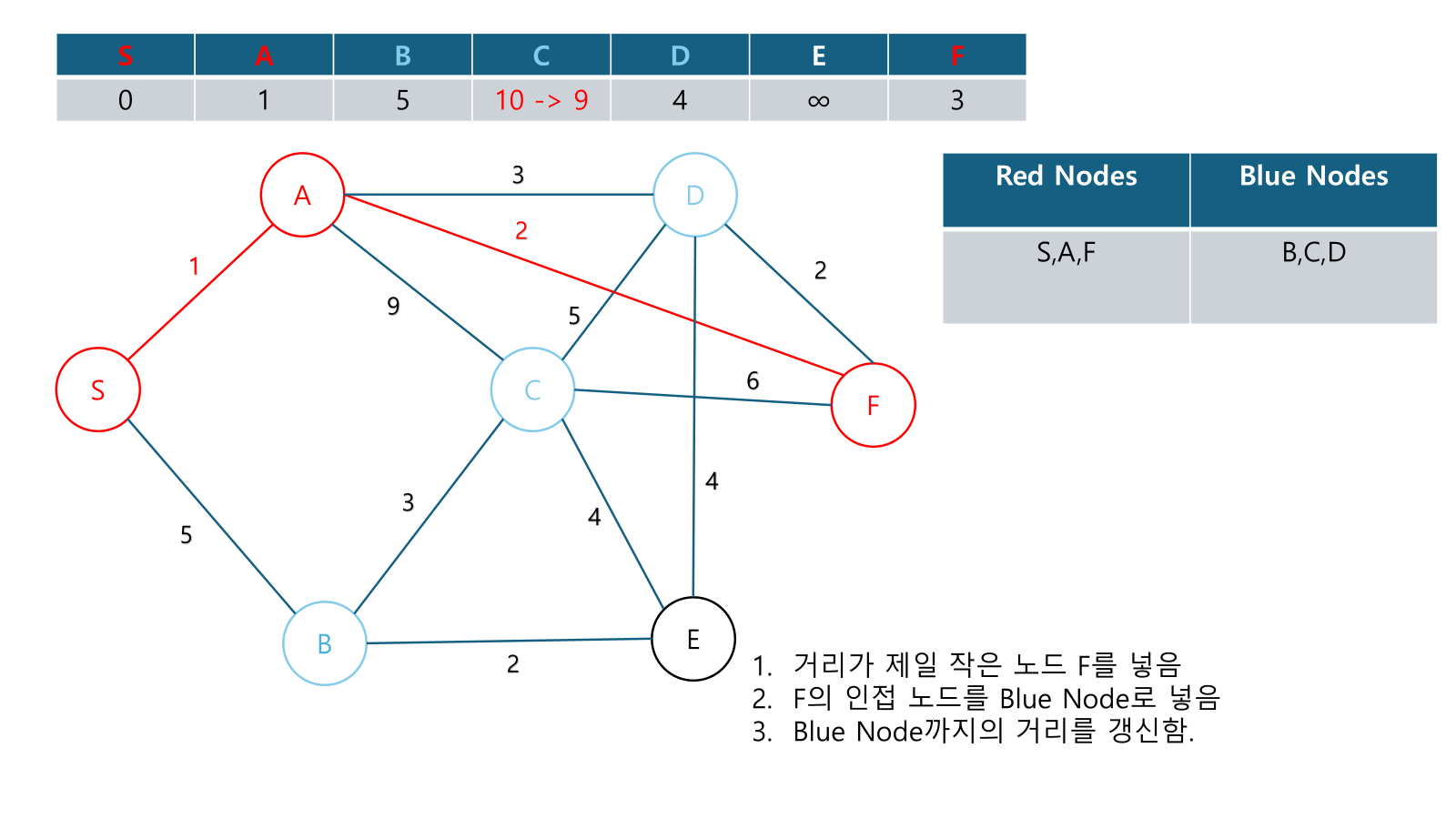
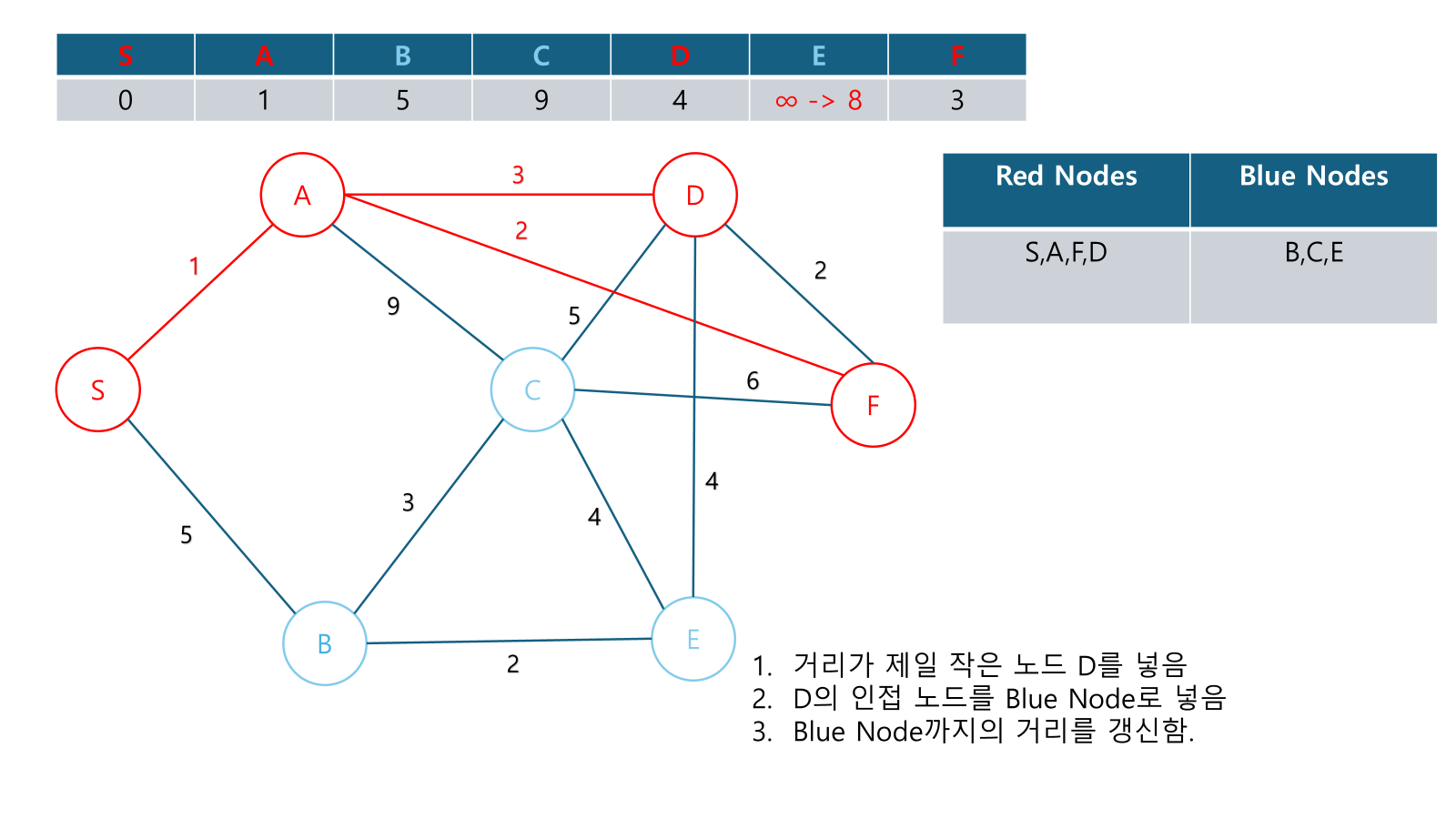
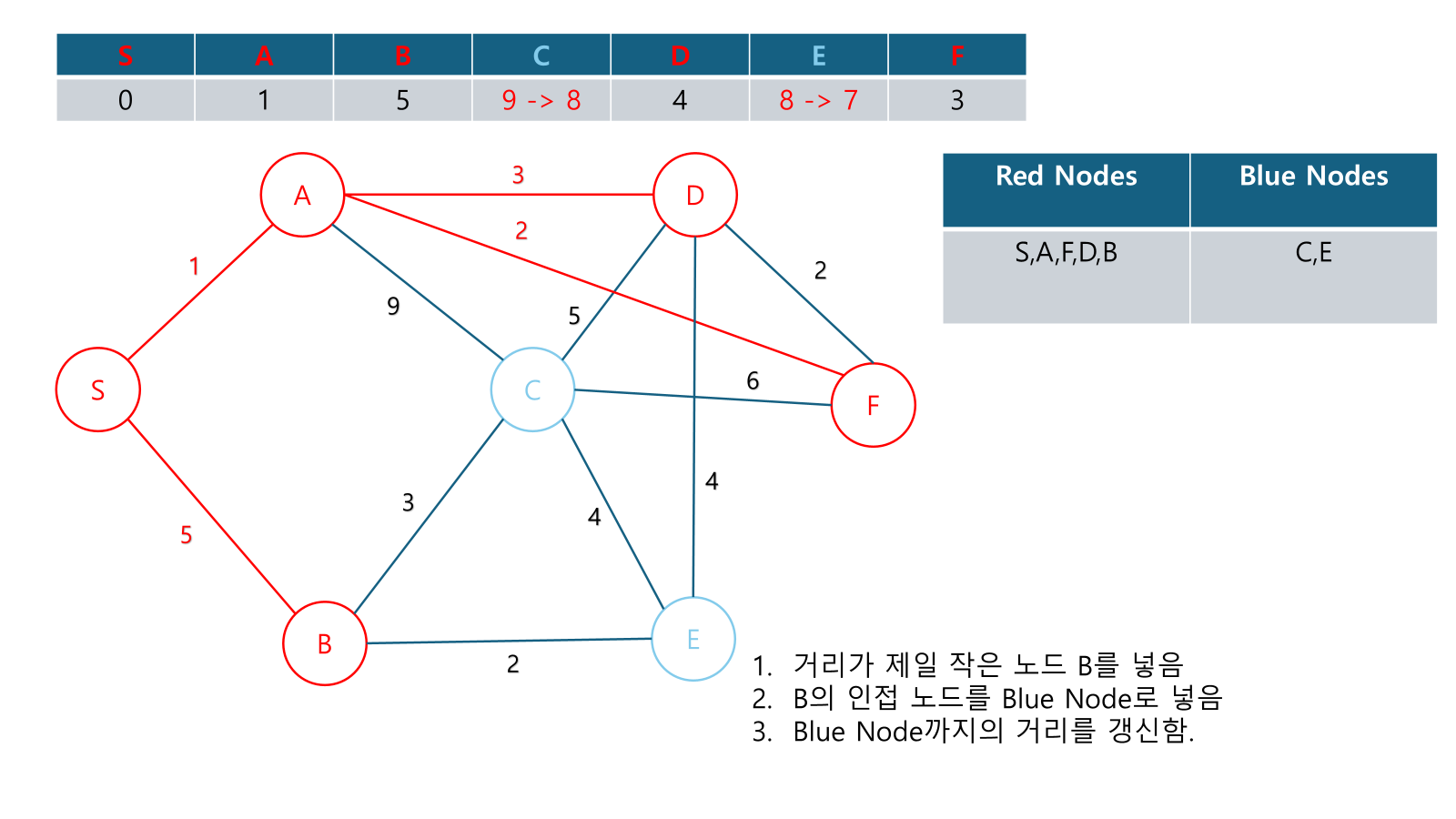
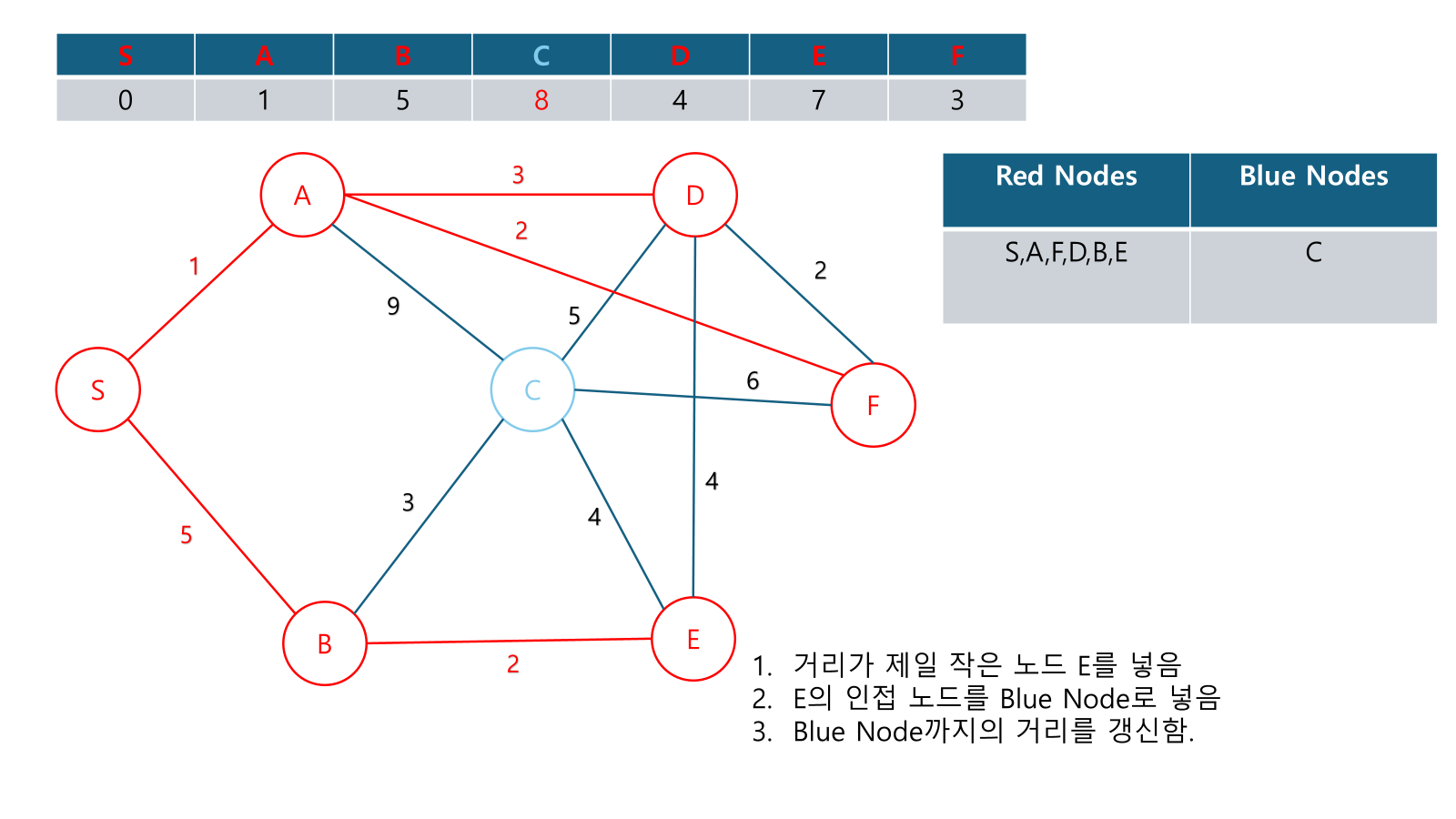
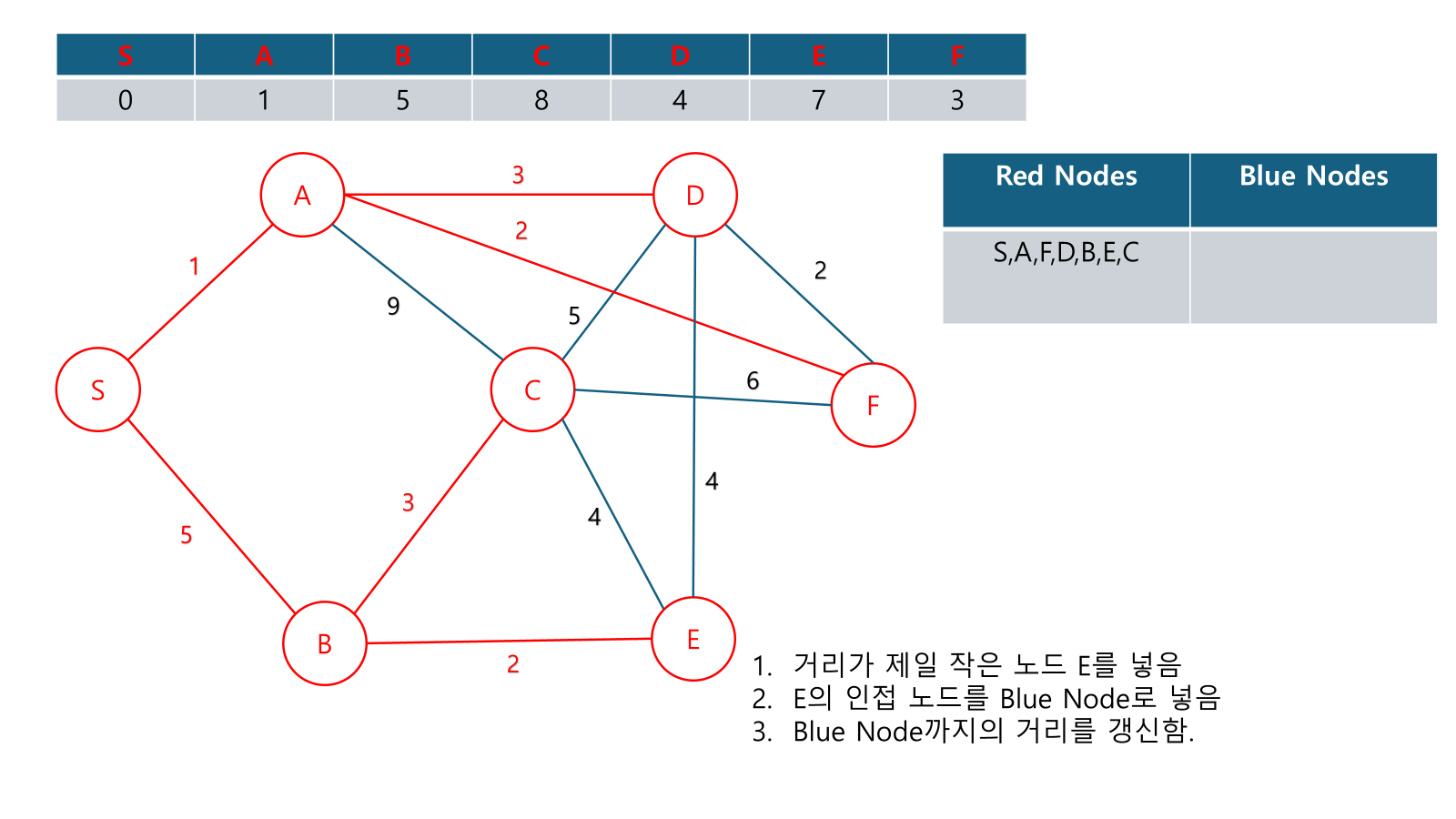
Alternate Explanations

As a Variations of BFS

BFS를 변형했다고 생각하면 됨. weight만큼 공간을 넣고 먼저 도착하는 거로 하기. 다만 구현에 문제가 있음

Select form Nearest to Furthest

다익스트라는 항상 작은 거 부터 큰 거로(가까운 거부터 먼 거로) 찾는다. 왜인가? 빨간 집합이 있고 vi와 그 뒤에 들어온 vi+1이 있다면

• $d_{i+1} > d_i$. 왜냐면 만약 $d_{i+1} < d_i$면 $v_{i+1}$이 v_i보다 빨리 들어가야 하기 때문.
• 또한 $d_{i+1}$의 값이 변하려면, $d_{i}$때문에 변했어야 하는데, $d_{i}+g(u,w)>=d_i$이기 때문에 성립
• 그 후 빨간 노드들과 파란 노드들 사이의 경계를 넘어오는 edge만 보면 됨 다른거는 볼 필요도 없음