Decoder와 Encoder

난1렙이요·2024년 10월 20일

컴퓨터 회로

목록 보기

15/15

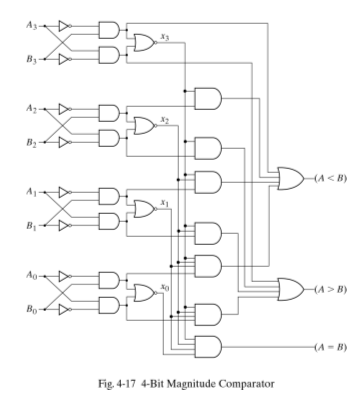
Magnitude Comparator

Magnitude Comparator는 숫자의 크기를 비교하는 회로다.
숫자 체계에서 MSB와 LSB가 있는데, MSB부터 순서대로 비교하여 숫자의 대소를 비교하는 장치이다.
$A = A_{3}A_{2}A_{1}A_{0}$
$B = B_{3}B_{2}B_{1}B_{0}$

$x_{i} = A_{i}B_{i} + A’_{i}B’_{i} = A_{i} \bigoplus B_{i}$

$(A=B)=x_{3}x_{2}x_{1}x_{0}$
$(A>B)=A_{3}B'_{3} + x_{3}A_{2}B'_{2} + x_{3}x_{2}A_{1}B'_{1} + x_{3}x_{2}x_{1}A_{0}B'_{0}$
$(A<B)=A_{3}B_{3} + x_{3}A'_{2}B_{2} + x_{3}x_{2}A'_{1}B_{1} + x_{3}x_{2}x_{1}A'_{0}B_{0}$

Decoder

옛날에 프린터는 출력기가 아닌 글자를 읽어내 복사하는 방식으로 쓰였다. 프린터가 이런 역할을 하려면 각각의 문자를 검출하는 과정이 필수였다. 문자를 검출하게 해주는 기계를 decoder라고 부른다.

decoder의 역할

$n-to-2^n$ decoder는 n-bit 입력에 대해 $2^n$ 의 출력을 내주는 기계이다. $2^n$ 의 출력 중 1이 되는 것은 오직 하나만 존재한다.

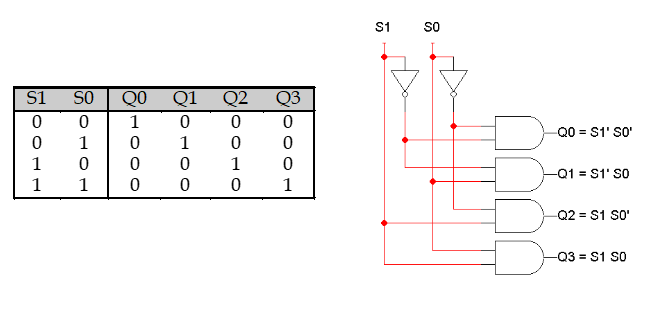
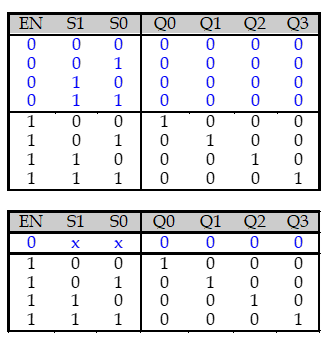
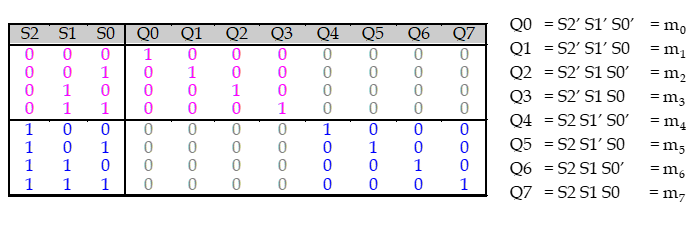
$2-to-4$ decoder는 2-bit입력에 대해 4개의 출력을 내주는 기계이다. 진리표는 다음과 같다.

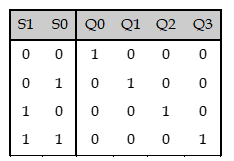
입력이 숫자 $i$ 라면, $Q_{i}$ 가 1이 된다(출력된다).
예시로, $S_{1}S_{0} = 10_{2}(+2)$ 에서 입력은 2이므로 $Q_{2}$ 는 1이 되며 나머지는 0이 된다.

모든 케이스에 대해 정리하면 다음과 같다.
$Q_{0} = S'_{1}S'_{0}$
$Q_{1} = S'_{1}S_{0}$
$Q_{2} = S_{1}S'_{0}$
$Q_{3} = S_{1}S_{0}$

그대로 회로로 옮기면 다음과 같은 회로가 만들어진다.

Enable inputs

Enable input은 회로를 동작시키겠다는 신호를 주는 입력이다. 만약 EN = 1이면 해당하는 decoder는 작동하며, EN = 0이면 decoder는 동작하지 않는다.

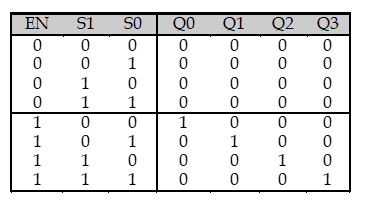
앞에서 배운 상관없음 기호를 통해 다음와 같이 진리표를 작성할 수 있다.

Blocks and abstraction

어려운 회로를 굳이 나타낼 필요 없이 Block으로 사용하면 편하다.

$EN, S_1, S_0$ 의 입력신호를 받는다.
$Q_3, Q_2, Q_1, Q_0$ 의 출력 신호를 보낸다.
순서를 바꾸면 안된다.

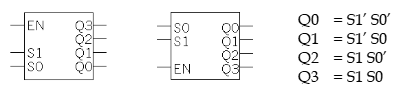
앞이 올바른 예, 뒤가 잘못된 예
또한 Block Symbol을 가지고 사용할 땐 기본적인 논리를 적어놔야 한다. 오른쪽이 기본적인 논리를 적어놓은 것이다.

Block을 사용하면 회로를 어렵게 말하지 않아도 연산을 수행할 수 있다. 다시 말하면 안이 어떻게 짜여져 있는지를 몰라도 사용할 수 있다. 함수의 역할을 하는 것이다. 이러한 특성때문에 재사용이 쉬워진다.

3-to-8 decoder

기본적인 골조는 같다.

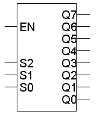
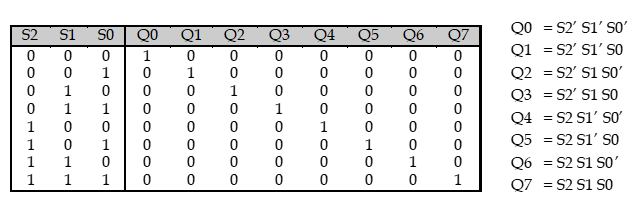
decoder는 복잡한 회로의 작은 부분을 담당하는 범용적인 회로이다. 이 decoder를 사용하면 모든 회로를 decoder로 표현할 수 있다. 이러한 특징때문에 minterm generators라고 불린다.

Design example : addition

Full Adder(전가산기)를 decoder로 설계해보자.

$X,Y,Z$ 3개의 input을 가진다.
$C,S$ 2개의 output을 가진다.
Full Adder의 진리표와 output에 대한 sum-of-minterm식을 아래와 같이 나타낼 수 있다.

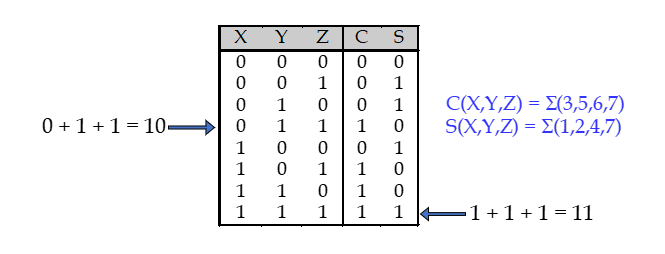
이를 통해 minterm들을 알아낼 수 있다. decoder의 각 output 신호에 맞게 연결하면 $C$ 과 $S$ 를 구현할 수 있다.

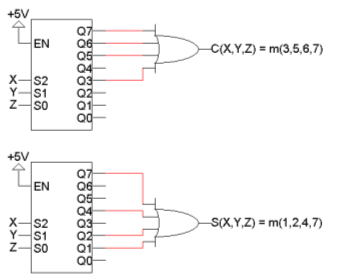
이 때 $+5V$ 를 통해 Enable input을 구현한다. 만약 $+5V$ 보다 많은 전압이 들어오면 활성화 된다. 다시말해 Enable input이 1이 된다.

위 그림에서 Decoder를 여러개 쓸 필요가 없다. 그러므로 Decoder를 하나로 줄이면 아래 그림과 같이 나온다.

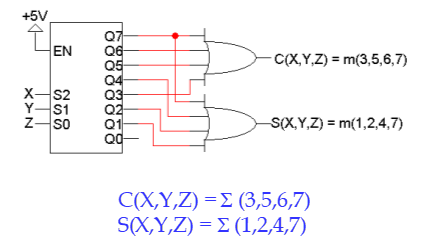
여기서 3-to-8 decoder를 사용하기보단 2-to-4 decoder를 2개 사용하여 구현하는 방법이 있다.

입력의 최상위인 $S_2$ 가 0이면 아래부분은 작동하지 않으며, $S_2$ 가 1이면 윗부분은 작동하지 않는다. 다시 말하면 $S_2$ 는 Enable input의 역할을 할 수 있다.

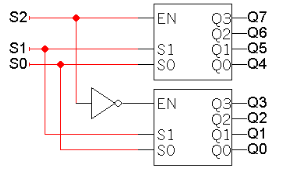
또한 mapping을 잘해줘야 한다. 3-to-8 decoder에서는 $S_2$ 가 2-to-4 decoder에서는 EN으로서 작동한다. 외부 회로와 내부 회로를 연결해 줄 때 잘못 연결하거나 구분해서 사용하지 않으면 안된다.

Encoder

decoder가 각각의 문자를 검출한다면 encoder는 검출된 결과물을 문자로 바꿔주는 역할을 한다. 다시 말하면 encoder는 decoder의 반대 개념이다.

encoder의 역할

$2^n-to-n$ encoder는 $2^n$ 입력에 대해 n-bit의 출력을 내주는 기계이다.

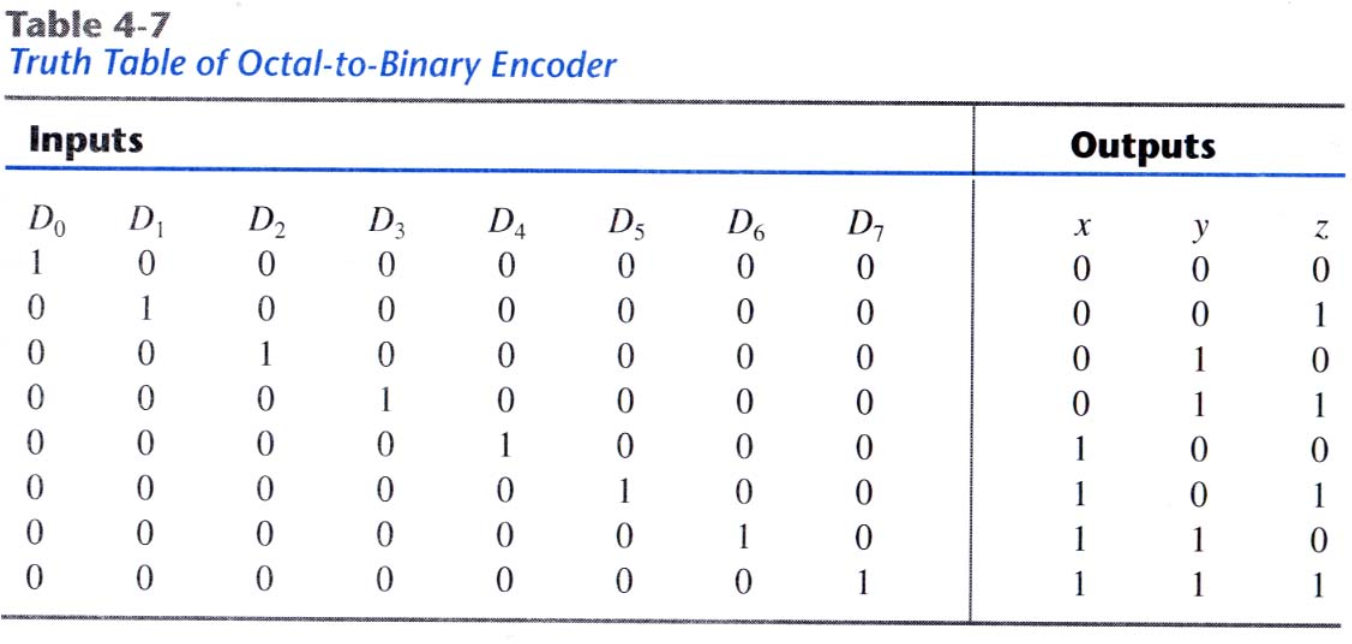
8진수-to-3진수 변환 encoder의 진리표는 다음과 같다. $3-to-8$ decoder의 정반대 역할을 한다.

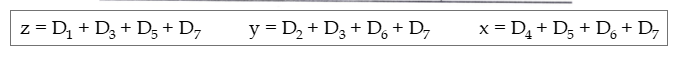
Ambiguity of Encoder

Encoder는 모호성을 가진다. Encoder는 입력으로 오직 하나의 1만 받았을 때 올바른 출력은 내지만, 만약 입력 중 1이 여러개거나 없으면 문제가 생길수 있다.

입력 중 1이 여러개 있는 경우에는 입력간에 우선순위를 두어서 1인 입력 중 우선순위에 따라서 출력을 낸다.
입력 중 1이 없으면 두 가지 방법이 있다.
- $D_0$ (맨 처음 입력)을 1로 만든다.
- $V$ 라는 신호를 두어서 모든 입력이 0이면 값을 출력하지 않는다.

Example

다음은 4-to-2 encoder이다.

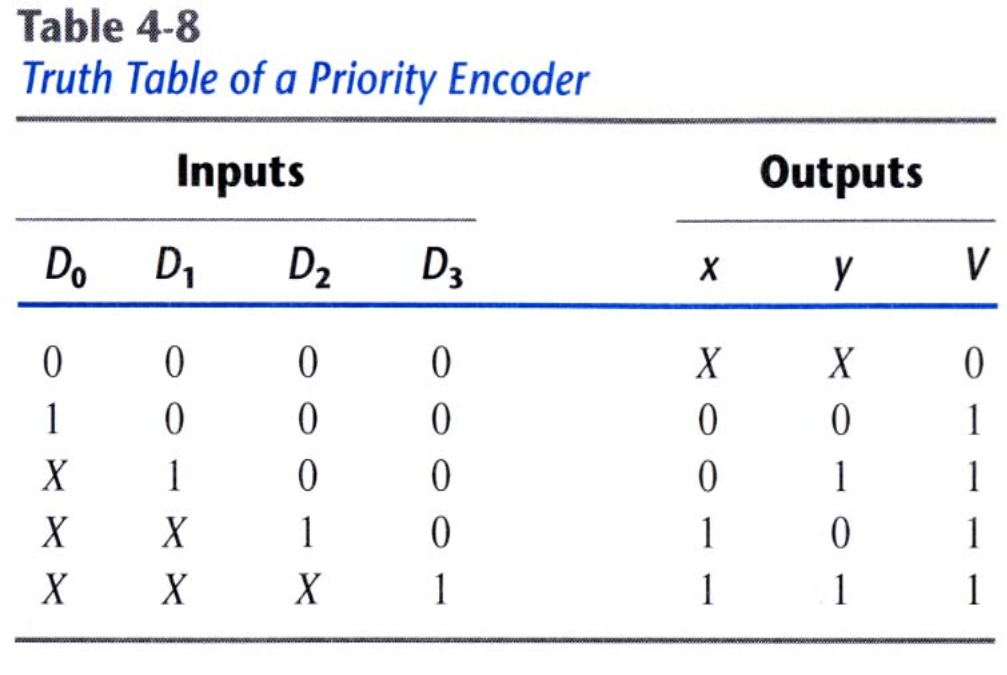
여기서 V를 통해서 모든 입력이 0이면 출력하지 않는 모습을 볼 수 있다.
또한 $D_0 < D_1 < D_2 < D_3$ 순으로 우선순위를 부여하는 모습을 볼 수 있다.

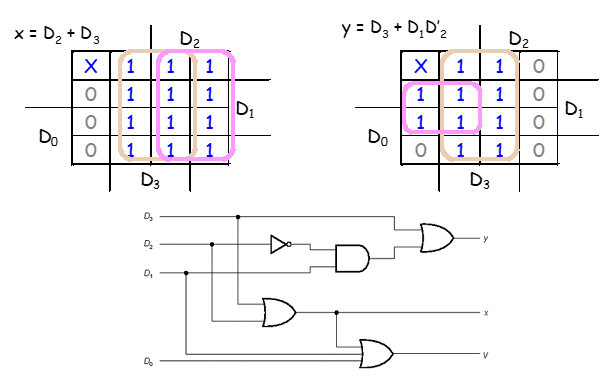
식을 정리하면 위와 같은 모습이 나온다.

인코딩과 디코딩

인코딩은 높은 차원의 자료를 낮게 만드는 효과가 있고, 디코딩은 낮은 차원의 자료를 높게 만드는 효과가 있다. 이를 통해 대용량 데이터에 대한 전달과 해석을 쉽게 할 수 있다.
만약 1920×1080 FHD모니터가 있다고 하자. 하나의 화소는 16-bit로 구성되어 있으며 30fps의 동영상을 재생한다고 하자. 필요한 데이터는 얼마나 될까?
먼저 1920x1080이므로 대략 화소가 $2 * 10^6$ 개가 필요하다. 그 후 화소 하나는 16-bit로 구성되어 있으므로 각각의 화소는 $2^{16}$ 의 데이터를 저장한다. 이 이미지를 30fps로 재생하므로 모두 합치면 1초에 $2 * 10^6 * 2^{16} * 30 = 3,932,160,000,000$ 이다... 어마어마하다. 당연히 이런 정보를 그냥 보낼 순 없으므로 많은 데이터를 인코딩을 통해 용량을 줄여주는 과정이 필요하다. 이 과정을 통해 줄여진 데이터를 디코딩을 통해 해석해줘야 하며 인코딩과 디코딩을 다른 방식으로 수행했다면 해석할 수 없으므로 같은 방식으로 수행해야한다. 이걸 수행하는 소프트웨어를 코덱(codec)이라고 부른다.