회로의 곱하기 연산

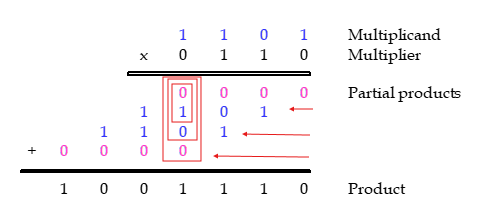
이진수의 곱하기 연산

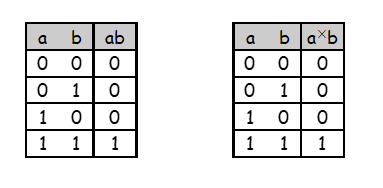
이진수의 곱하기 연산은 더하기 연산과 비슷하다. 그러므로 전가산기만 가지고 있으면 곱하기 또한 구현할 수 있다. AND연산이라는 것은 기본적으로 a와 b에 대한 곱셈 연산이므로, AND연산을 활용하면 곱하기를 쉽게 구현할 수 있다.

곱셈은 곱해지는 수(Multiplicand)와 곱하는 수(Multiplier)가 있다.

• Multiplier의 자리수가 0이면 무시한다.
• Multiplier의 자리수가 1이면 자신의 자리수에 맞게 Multiplicand를 복사한다.
• 모두 수행했으면 각각의 자리수마다 AND연산을 수행한다.
  

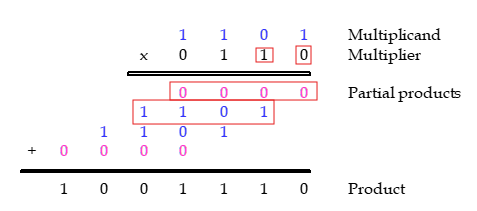
여기서 덧셈은 얼마나 해야 할 까? 위의 예시를 보면 제일 연산이 많은 가운데는 3번의 연산을 하게 된다.

• $1 + 2$
• $1 + 2 + 3$
• $1 + 2 + 3 + 4$
  

그러므로 N-bit 곱하기 연산에서는 N-1개의 전가산기가 있으면 된다.

---

곱하기의 조합회로

간단한 거부터 해보자

2X2 곱하기

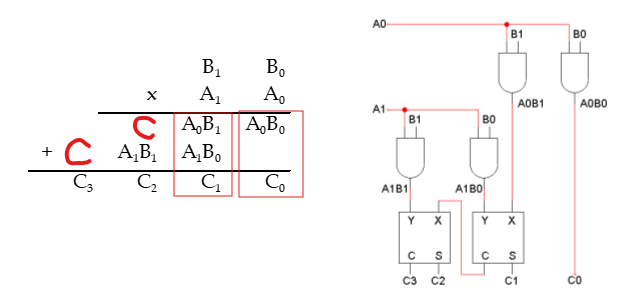
• 처음 값은 $C_{0} = A_{0}B_{0}$다.
• 두번째 자리수는 전가산기를 통해 $A_{0}B_{1} + A_{1}B_{0}$연산을 한다.
• 두번째 값 $C_{1} = S$가 된다.
• 세번째 자리수는 전가산기를 통해 $C + A_{1}B_{1}$연산을 한다.
• 세번째 값 $C_{2} = S$가 된다.

위 회로에서 $C$는 carry가 아니라 결과값이다. 혼동하면 안됨.

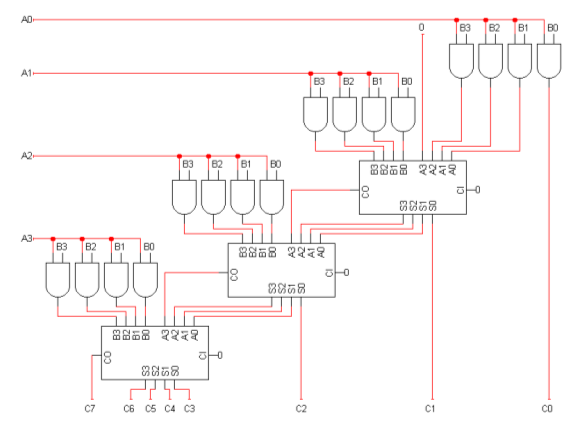
4X4 곱하기

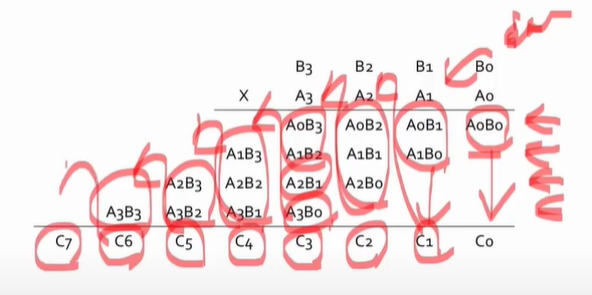
복잡해 보이지만 앞에서 말한 내용의 응용이다.

곱셈기의 문제

곱셈기는 n-bit 연산에 대해서 2*n-bit의 결과를 내게 된다. 또한 전가산기가 n-1개 필요하게 된다. 이는 bit가 작을 때는 문제가 되지 않지만 비트가 커지면 회로가 복잡해지는 문제가 생긴다.

곱셈의 특별한 경우

10진수에서, 10을 곱한다는 의미는 원래 숫자를 왼쪽으로 한 칸 민다는 의미랑 동일하다. 이는 모든 진수 시스템에서 통용될 수 있다. n진수 시스템에서 n을 곱한다는 의미는 원래 숫자를 왼쪽으로 한 칸 밀고 0을 추가하는 의미와 동일하다.
예를 들어 $11_{2}(+3) * 10_{2}(+2) = 110_{2}(6)$이 되는데, 이는 원래 숫자를 한 자리 이동시키고 0을 붙혀주는 연산과 동일하다.