회로는 대체로 연산의 level이 적을 수록 성능이 올라간다. 이러한 회로의 level을 최소화하려면 Sum of product의 방법이 쓰이는데, 이걸 minimal sum of product(MSP) 방법이라 하며, 이를 통해 두개의 방법을 가진 회로로 만들 수 있다.
Karnaugh maps(K-maps)
진리표로부터 만들어내기

일단 진리표로부터 minterm을 추출해낸 뒤, 표에 minterm들을 배치한다. 배치 순서는 왼쪽 위에서부터 0이고, 오른쪽 아래로 점차 1로 바뀌어간다.
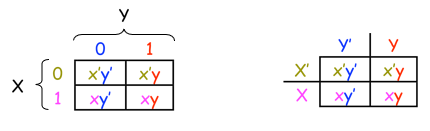
이제 minterm들끼리 공통된 신호를 가지고 있는 것을 확인할 수 있다. 예를 들어, x'y'와 x'y는 x'라는 공통된 신호를 가지고 있고, x'y'와 xy'는 y'라는 공통된 신호를 가지고 있다. 이렇게 만들어낸 k-map을 통해서 공통된 신호를 뽑아낼 수 있다. 이걸 간략화 과정이라 부른다. 간략화 과정은 옆에 있는 minterm끼리 묶어서 수행할 수 있다.
x'y' + x'y = x'
x'y', x'y에 대한 sum이 있다고 가정했을 때, 공통된 신호는 x'다. 그러므로 y'와 y는 OR연산을 할 수 있고, 이는 x'만 남는 결과를 가져올 수 있다.
x'y + xy = y
x'y' + x'y + xy = (x'y' + x'y) + (x'y + xy) = x' + y
3개 변수에 대한 k-map

일단 첫번째로, x와 yz에 대해서 나눌 수 있다.
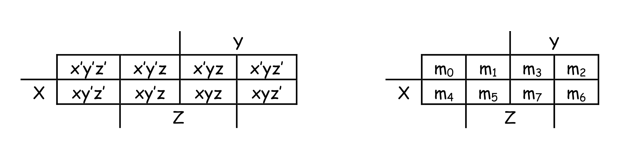
그 다음, 각각의 X,Y,Z로 또 나눈다.
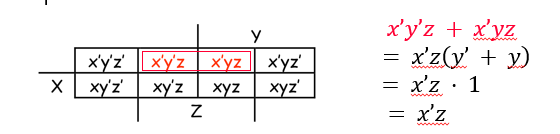
이 때, 10과 11의 순서가 바뀌어있다. 이는 yz의 배치 순서가 00, 10, 01, 11로 되어 있으면 옆에 있는 minterm끼리 묶었을 때 10과 01은 접점이 하나도 없으므로 순서를 바꿔줌으로써 간략화를 쉽게 할 수 있다.
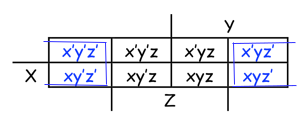
또한 양쪽 끝은 서로 연결되어 있기 때문에, 간략화 시킬 수 있으며 위 아래도 동일하다.
x'y'z' + xy'z' + x'yz' + xyz'
=z'(x'y' + xy' + x'y + xy)
=z'(y' + y)
=z'
활용
𝑓(𝑥,𝑦,𝑧) = 𝑥𝑦 + 𝑦’𝑧 + 𝑥𝑧라는 함수가 있다. 이 함수의 진리표는 다음과 같다.
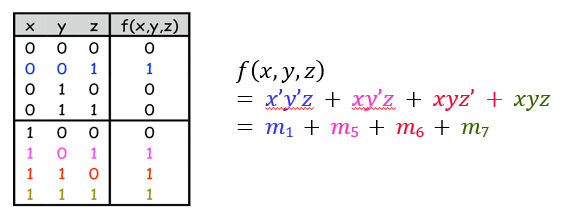
xy에 해당하는 m6과 m7 / y'z에 해당하는 m1과 m5 / xz에 해당하는 m5와 m7 모두를 OR연산한다. 결과는 𝑓(𝑥,𝑦,𝑧) = m1 + m5 + m6 + m7으로 나온다.
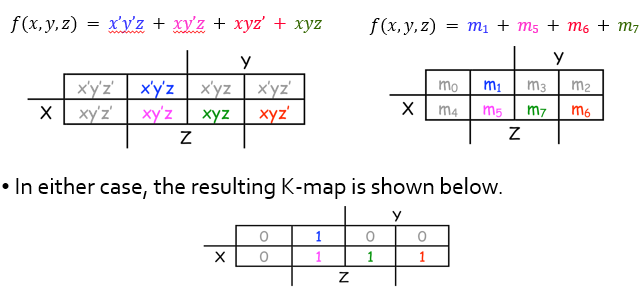
이제 k-map을 통해서 간략화를 시행한다. x'y'z + xy'z == y'z / xyz' + xyz == xy 이므로 𝑓(𝑥,𝑦,𝑧) = 𝑥𝑦 + 𝑦’𝑧 + 𝑥𝑧 = y'z + xy
다른 예시
𝑚1 + 𝑚3 + 𝑚5 + 𝑚6
(m1 + m3) + (m1 + m5) + m6
x'y'z + x'yz == x'z / x'y'z + xy'z == y'z
x'z + y'z + xyzminterm을 묶기
k-map을 이용해서 간략화하는 과정에서 제일 어려운 부분이다. minterm들을 직사각형 형태로 묶으며, 2^(n-1)개 만큼 묶는다.
- 간략화를 통해 마지막에 나오는 식의 개수를 최대한 줄여야 한다.
- 직사각형을 최대한 크게 묶어서, 입력 변수를 최대한 줄여야 한다.
Prime Implicants(주항목)
- Prime implicant(주항목) : 간략화를 통해 묶은 사각형들 중 가장 크게 묶은 사각형을 Prime implicant(주항목)라고 말한다.
- Essential prime implicant(필수 주항) : 자기 자신의 주항목에만 속하고, 다른 주항목에 속하지 않는 주항목을 Essential prime implicant(필수 주항)라고 말한다. 필수 주항이 아닌 주항목은 표현 방식이 달라질 수 있지만, 필수 주항은 무조건 하나의 표현 방식을 갖는다는 점에서 중요하다.
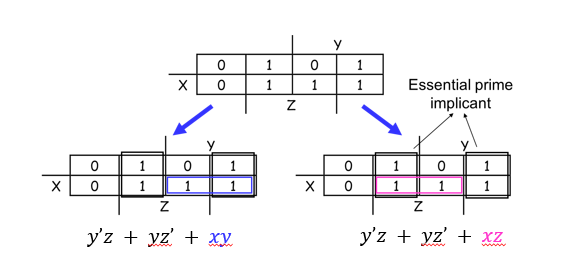
- K-map을 통해서 간략화 하는 과정을 하다보면 답이 여러개가 나올 수 있다. 필수 주항을 가지고 있고 필수 주항이 아닌 주항목이 식에 맞게 나와있다면 그 답은 맞다고 할 수 있다.
Product of Sum 형식으로 나타내기
지금까지 우리는 SOP형식으로 나타냈다. SOP와 POS는 쌍대성이므로 SOP형식으로 나타낸 식들은 모두 POS로 나타낼 수 있다.
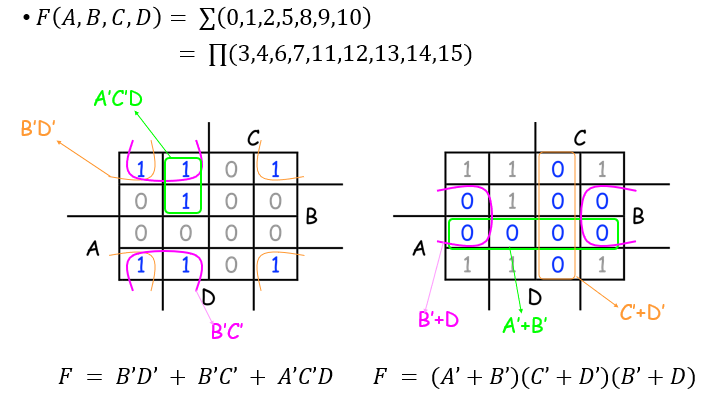
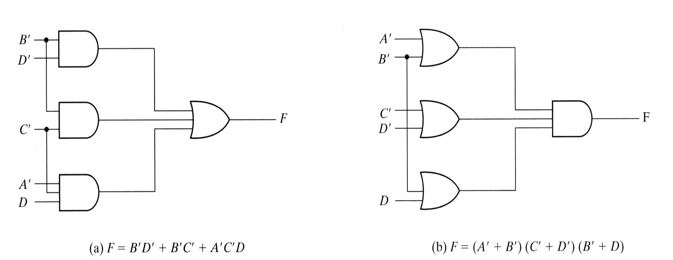
왼쪽에 있는 게이트들은 맨 마지막이 3-input gate다. 그러나 오른쪽에 있는 게이트는 모두 2-input gate다. 굳이 따지자면 오른쪽이 간략화가 더 잘 되었다고 할 수 있다.
Don't Care Condition
회로에서는 다음과 같은 상황이 있을 수 있다.
- 어떠한 입력이 절대 들어올 일이 없을 때
- 어떤 출력이 그 회로에서 다시는 재사용될 일이 없을 때
해당하는 조합을 Don't Care Condition으로 부르고 X로 표시한다.
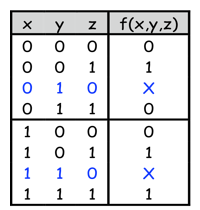
이 경우에 해당하는 조합을 0 또는 1 어느 것으로 하든 상관이 없다. Don't care Condition을 통해 더욱 자유도가 높은 간략화를 할 수 있게 된다.
Example : Seven Segment Display
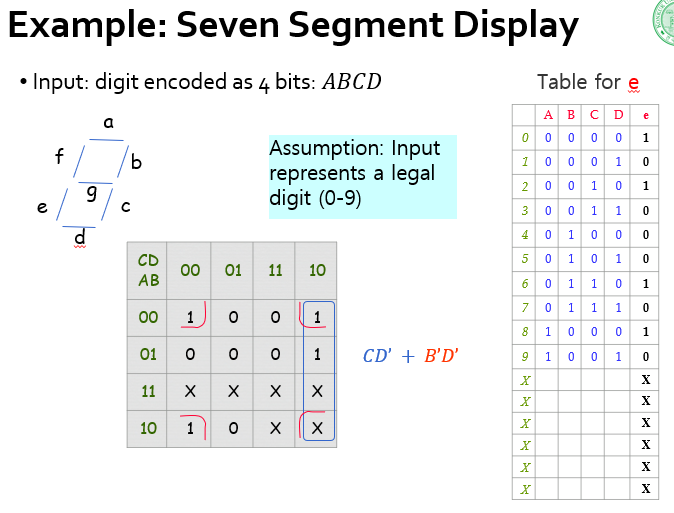
K-map 정리
k-map은 회로를 간단화 할 수 있는 방법이다.
- 결과는 SOP(sum of products)로 나오며, 이를 통해 two-level 회로를 만들 수 있다.
- don't card conditions를 다루기 쉽다.
- K-map은 변수가 적을때 편하지만, 변수가 5~6개 이상이면 간략화 하기 어려워진다.(3차원으로 들어가기 때문임)
k-map으로 간략화를 할 때는 다음을 기억해야 한다.
- 알맞은 순서를 따라야 한다. = 0132등등...
- 양쪽 귀퉁이에 있는 것도 그룹화 할 수 있다.
- 제일 큰 사각형을 기준으로 간략화를 해야 한다.
- 간략화의 결과는 여러개가 나올 수 있다. 등가 회로이기 때문에 모두 정답이다.
