NAND Gate와 NOR Gate의 효율성

NAND 게이트와 NOR 게이트는 AND나 OR보다 회로를 설계할 때 더 자주 쓰인다. 둘은 다음과 같은 이점을 가진다.

• 성능
• 비용

NAND 회로

NAND로 Inverter(NOT), AND, OR를 만들 수 있다.

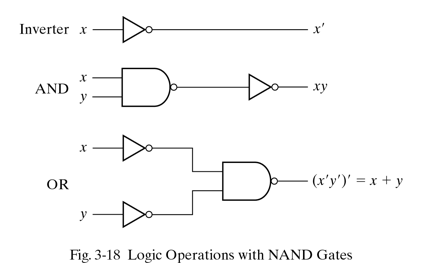
이러한 특성때문에 범용 게이트(Universal Gate)라고 불리기도 한다.

NAND 게이트의 표현 방법

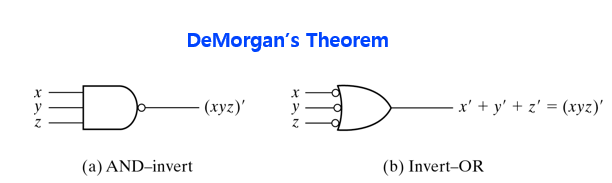
NAND 게이트는 2가지로 표현 가능하다.
AND invert : $(xyz)'$
Invert-OR : $x'+y'+z' = (xyz)'$

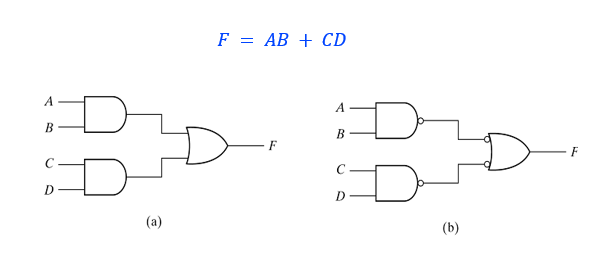
NAND로 바꾸기

모든 AND는 AND-invert로 바꾸고, 모든 OR은 Invert-OR로 바꾼다. 이를 쉽게 하는 방법은, 게이트의 출발과 다음 도착 지점 두 지점에 bubble(NOT)을 붙히는 것이다. NAND와 NOR로 쉽게 바꾸면서 회로를 유지할 수 있다.

NOR 회로

NAND로 Inverter(NOT), AND, OR를 만들 수 있다.

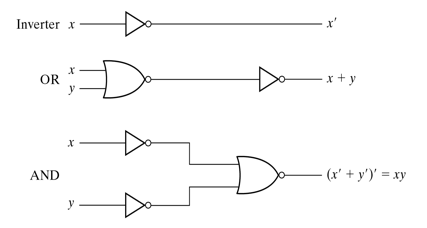
이러한 특성때문에 범용 게이트(Universal Gate)라고 불리기도 한다.

NOR로 바꾸기

모든 AND는 Invert-OR로 바꾸고, 모든 OR은 OR-invert로 바꾼다. 이를 쉽게 하는 방법은, 게이트의 출발과 다음 도착 지점 두 지점에 bubble(NOT)을 붙히는 것이다. NAND와 NOR로 쉽게 바꾸면서 회로를 유지할 수 있다.

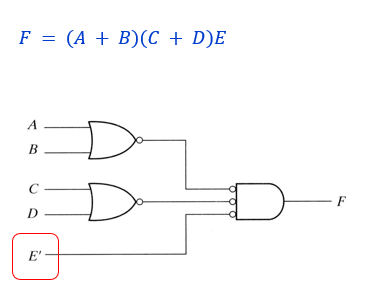
AND-OR-Invert

sum of product를 표현할 때 여러가지 게이트로 표현할 수 있다. 예를 들어 AND-NOR를 사용하는데 지금 NAND와 AND밖에 없다면 다음과 같이 구현할 수 있다.

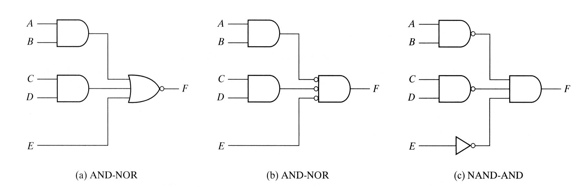
AND-NOR = NAND-AND

OR-NAND-Invert

prodcut of sum을 표현할 때 여러가지 게이트로 표현할 수 있다. 예를 들어 OR-NAND를 사용하는데 지금 NOR와 OR밖에 없다면 다음과 같이 구현할 수 있다.

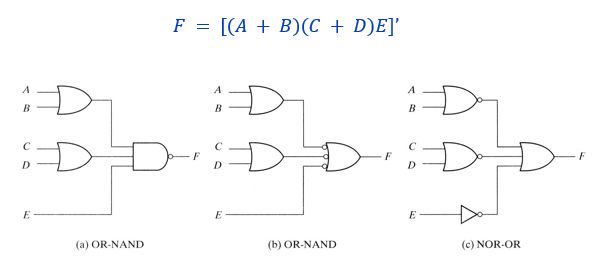
OR-NAND = NOR-OR

Exclusive-OR Function

Exclusive-OR : $x⨁y = xy' + x'y$
Exclusive-NOR : $(x⨁y)' = xy + x'y'$
속성

• $x⨁0 = x$
• $x⨁1 = x'$
• $x⨁x = 0$
• $x⨁x' = 1$
• $x⨁y' = x'⨁y = (x⨁y)'$
• $A⨁B = B⨁A$
• $(A⨁B)⨁C = A⨁(B⨁C) = A⨁B⨁C$

Odd Function

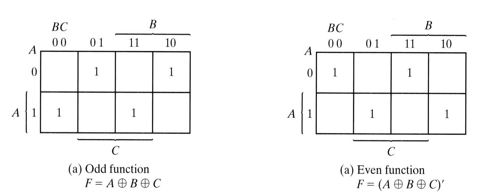
Exclusive-OR은 들어오는 1의 개수가 홀수이면 1이고, 짝수이면 0을 내주는 역할을 해준다. 홀수/짝수를 구분해준다는 점에서 Odd Function이라고 불린다.

Parity Generation and Checking

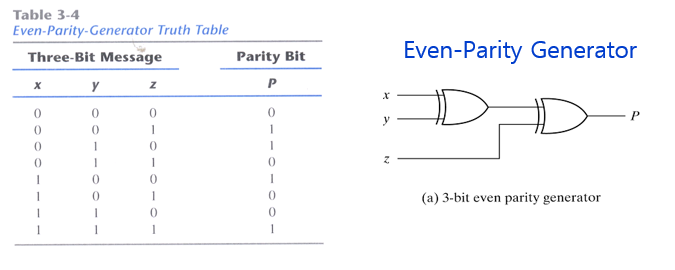
이진 연산에서 자신의 자리수를 정하는 방법으로 Parity를 배웠다. Exclusive-OR를 이용하여 이진 Parity를 쉽게 생성할 수 있다.