Matrix Multiplication

Matrix Multiplication

Problem

• $M_1, M_2, ... , M_n$의 배열들이 있다.
• $M_{k-1}$이 $n*m$ 크기의 배열이라 할 때, $M_{k}$는 $m*l$ 크기의 배열이다.
• 이 때 계산 순서에 따라 결과물의 계산 시간이 달라진다.
• 예를 들어 $3 * 5, 5 * 1, 1 * 6$ 배열이 있다고 가정하자.
• 앞부터 계산하면 $3 * 5 * 1 + 3 * 1 * 6$
• 뒤부터 계산하면 $5 * 1 * 6 + 3 * 5 * 6$
• 계산량이 가장 적은 순서를 찾아보자.

Idea

• $M_n$의 크기는 $d_{n-1}, d_n$이라고 할 수 있다.
  • $M_{n-1}$의 크기는 $d_{n-2}, d_{n-1}$이라고 할 수 있다. 이는 배열의 곱하기를 가능하게 한다.
• $M_i, ... , M_j$에 대해서 모든 경우의 수를 다 계산한다.
• $d[i][j]$를 모두 계산하여 적어논다.
• $...(M_i, ... ,M_j)...$에서 밖의 요소들은 안에 영향을 주지 않는다.

Example

• $M_1, M_2, M_3, M_4, M_5$개의 배열이 있다고 가정하자
• $M_1 * M_2 * M_3 * M_4 * M_5$의 계산을 수행한다.
• 이 때 $M_1 * M_2$를 맨 처음 계산하는 방법은 $M_1 * M_2$의 크기 + $M_2 * M_3 * M_4 * M_5$의 크기와 같다.

Algorithm

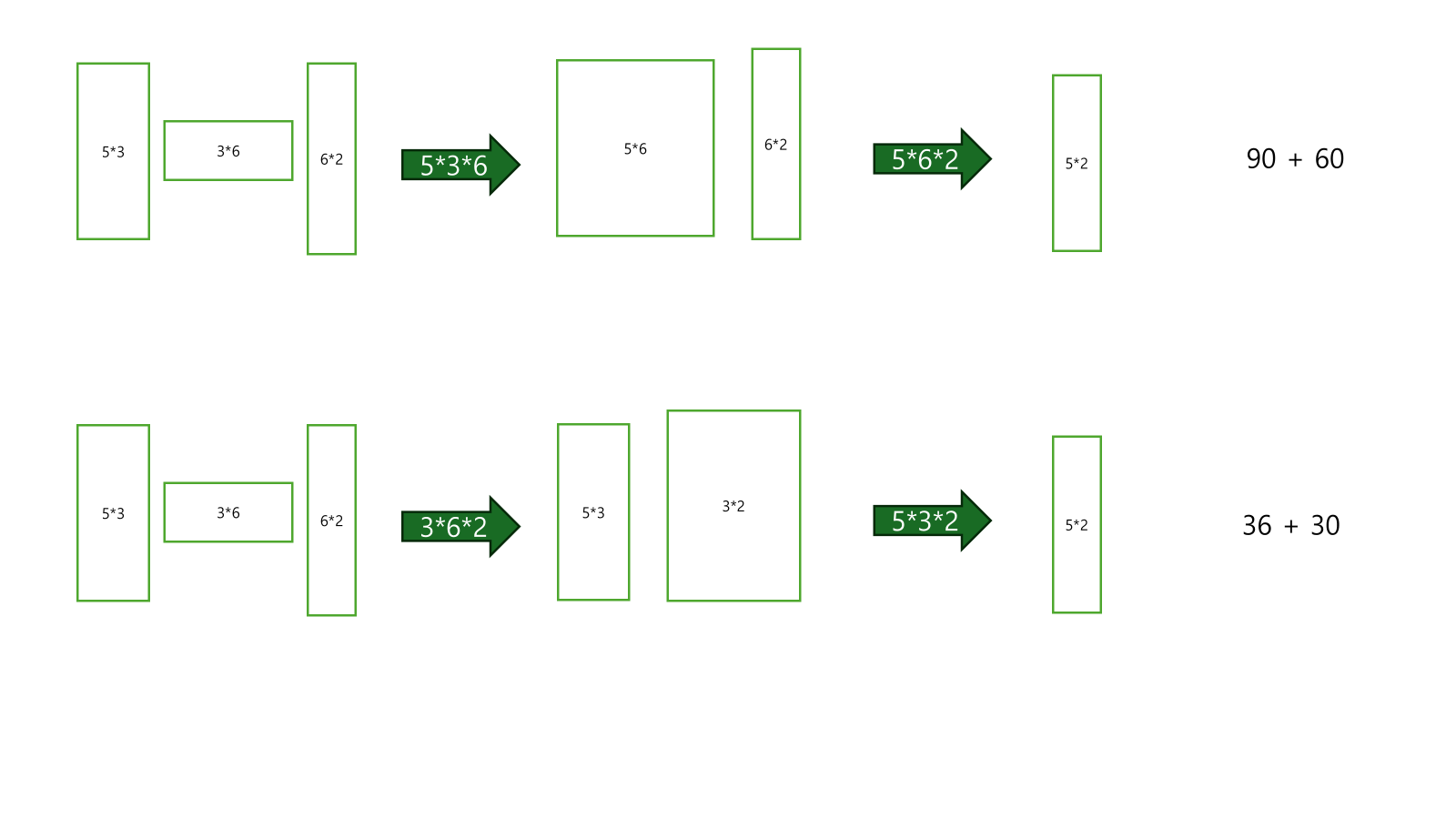
• $d[i][i]$는 0이다.
  • 자신에 자신을 곱하는 건 시간이 들지 않는다.
• $d[i][i+1]$는 $d_{n-1} * d_{n} * d_{n+1}$이다.
  • 배열 $M_i * M_{i+1}$이다
  • 배열 $M_i$의 크기는 $d_{n-1}, d_n$
  • 배열 $M_i$의 크기는 $d_n, d_{n+1}$
  • 그러므로 $d_{n-1} * d_{n} * d_{n+1}$
  • 이 말은 곱하기 하나짜리는 모두 구할 수 있다는 뜻이다.

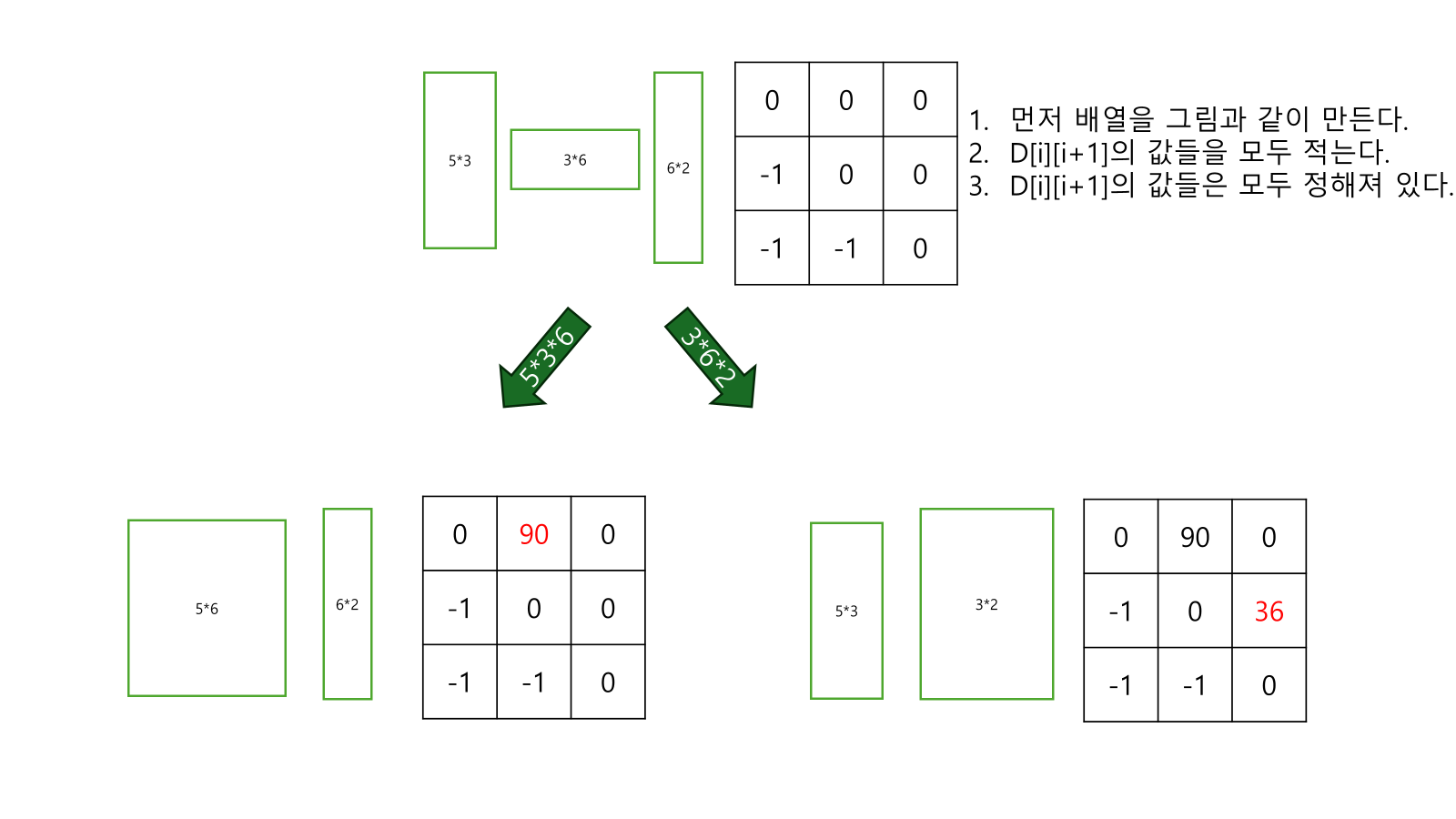
• $d[i][i+2]$는 $d[i][i+1] + d[i+1][i+2]$
  • 이 말은 곱하기 하나짜리가 계산되어 있음이 보장이 되어 있을 때 확장이 가능하단 뜻이다.
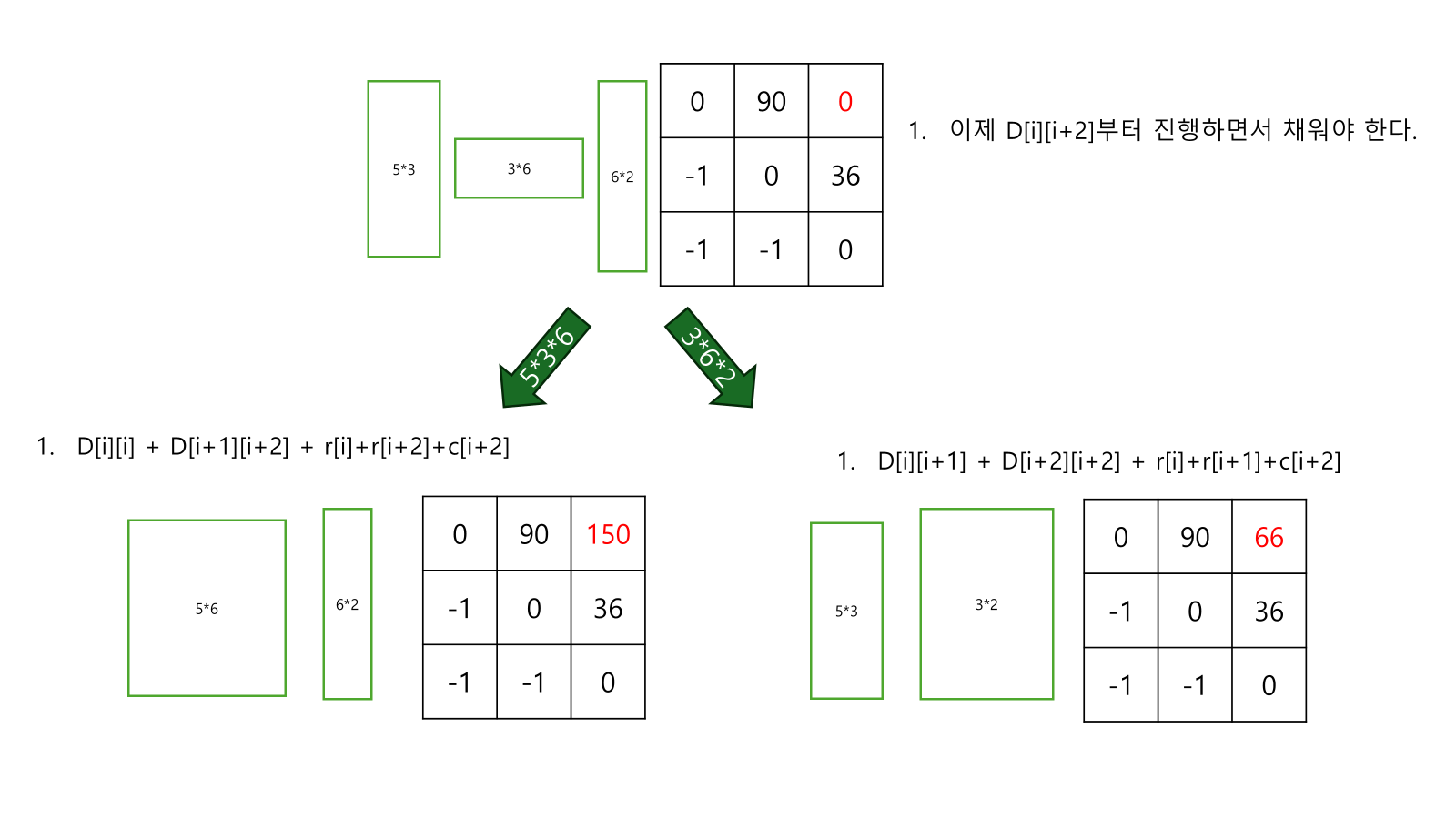
• $d[i][i+k]$는 최소값을 구하면 되는데...
  • $d[i][i+1] + d[i+1][i+k]$
  • $d[i][i+2] + d[i+2][i+k]$
  • ... $d[i][i+k-1] + d[i+k-1][i+k]$
  • 이 중 최소값이다.

예시 코드

행렬 곱셈 문제

import java.io.*;
import java.util.*;


public class Main {

    public static Scanner sc = new Scanner(new InputStreamReader(System.in));
    public static int N;
    public static int[][] D;
    public static int[] r;
    public static int[] c;

    public static void main(String[] args) throws IOException {

        //행렬 개수 N을 입력받음
        N = sc.nextInt();

        //N만큼 크기 설정함
        r = new int[N+1];
        c = new int[N+1];

        //A의 요소들을 입력받음
        for(int i=1; i<=N; i++){
            r[i] = sc.nextInt();
            c[i] = sc.nextInt();
        }

        //D는 배열 전체의 길이를 저장함
        D = new int[N+1][N+1];

        //Base
        for(int i=1; i<=N; i++){
            for(int j=1; j<=N; j++) {
                if (i == j) D[i][j] = 0;
                else D[i][j] = -1;
            }
        }

        //Step
        //D[i][j] = min(D[i][j-1]+r[i]*r[j]*c[j], D[i+1][j]+r[i]*c[i]*c[j])
        //k는 간격
        for(int k=1; k<N; k++){
            for(int i=1; i+k<=N; i++){
                int j=i+k;
                for(int l=1; l<=j-i; l++){
                    if(D[i][j]<0) D[i][j] = D[i][i+l-1]+D[i+l][j]+r[i]*r[i+l]*c[j];
                    D[i][j] = Integer.min(D[i][j], D[i][i+l-1]+D[i+l][j]+r[i]*r[i+l]*c[j]);
                }
            }
            //D[1][2] = D[1][1] + D[2][2] + r[1]*r[2]*c[2];
            //D[1][3] = min(D[1][1] + D[2][3] + r[1]*r[2]*c[2], D[1][2] + D[3][3] + r[1]*r[3]*c[3]);
        }

        System.out.println(D[1][N]);
    }
}