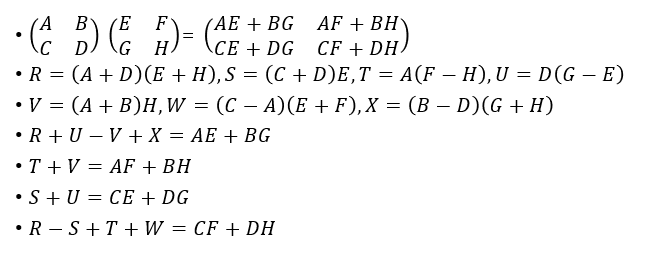Divide Conquer Others

Matrix Multiplication

2차원 $N^2$배열을 곱하는 과정은 $O(N^3)$의 시간이 소요된다.

• 한 칸을 만드는데 $O(N)$의 시간이 걸린다.
• 모두 $N^2$개가 있다.
• 그러므로 $O(N*N^2) = O(N^3)$

$O(N^3)$는 너무너무 느리다... 더 빨리 할 수 없을까?

곱하는 과정은 $O(N^2)$보다 빠를 수 없다. 배열을 만드는 과정이 $O(N^2)$가 걸리기 때문이다.

• Lower Bound : $O(N^2)$
• Upper Bound : $O(N^3)$

Use Divide and Conquer

$\left[ \begin{matrix} A & B \\ C & D \\ \end{matrix} \right]$ $\left[ \begin{matrix} E & F \\ G & H \\ \end{matrix} \right]$ = $\left[ \begin{matrix} AE+BG & AF+BH \\ CE+DG & CF+DH \\ \end{matrix} \right]$

$T(N) -> 2^3T(N/2) -> 2^6T(N/4) -> ...$
$O(N^3)$
효율성은 없지만 분리해서 생각할 수 있음을 확인하였다.

Strassen's Algorithm을 활용하면 변수를 7개로 줄일 수 있다.

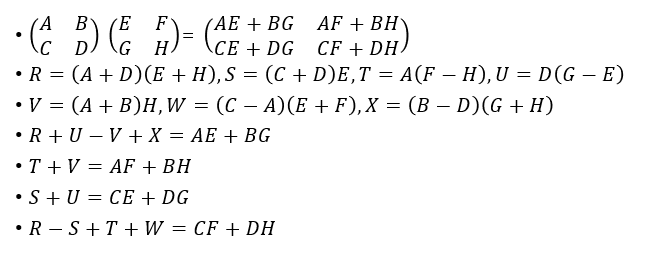
$T(N) = O(2^3log_{7}N) = O(N^{2.807})$

Karatsuba Algorithm

컴퓨터에서 곱하기는 나누기보다 빠르다.
n-bit끼리의 곱셈은 $O(N^2)$의 시간이 걸린다.
$O(N)$보다 빨라질 수 없는데, N만큼 더하기 때문.

• Lower Bound : $O(N)$
• Upper Bound : $O(N^2)$

$x_{1}B^{k} + x_{0} = x$
$y_{1}B^{k} + y_{0} = y$
$x_{1}y_{1}B^{2k} + (x_{1}y_{0} + x_{0}y_{1})B^{k} + x_{0}y_{0} = xy$
$(x_{1} + x_{0})(y_{1} + y_{0})$
$x_{1}y_{1} + (x_{1}y_{0} + x_{0}y_{1})+ x_{0}y_{0}$
$(x_{1}y_{0} + x_{0}y_{1}) = (x_{1} + x_{0})(y_{1} + y_{0}) - x_{1}y_{1} - x_{0}y_{0}$

$x_{1}y_{1}B^{2k} + (x_{1}y_{0} + x_{0}y_{1})B^{k} + x_{0}y_{0}$
$=x_{1}y_{1}B^{2k} + ((x_{1} + x_{0})(y_{1} + y_{0}) - x_{1}y_{1} - x_{0}y_{0})B^{k} + x_{0}y_{0}$

둘을 비교해보자.

• 앞의 방법은 $x_1y_1, x_1y_0, x_0y_1, x_0y_0$ 4개의 곱셈이 나온다.
• 뒤의 방법은 $x_1y_1, x_0y_0, (x_1+x_0)(y_1+y_0)$ 3개의 곱셈이 나온다.

곱셈을 4개에서 3개로 줄일 수 있다. 당연하지만 곱셈은 덧셈보다 시간이 오래 걸리므로 효율을 늘릴 수 있다.

Radix Sort

Radix sort는 기수(radix) 별로 비교 없이 정렬하는 정렬 알고리즘이다.

가령 문자들에 대해서 사전순으로 정렬해야 한다고 생각하자.

(cdc, acab, dda, cda, abcd, dab, bcbc)

첫번째 자리를 기준으로 정렬한다.

(acab, abcd, bcbc, cdc, cda, dda, dab)

두번째 자리를 기준으로 정렬한다.

(abcd, acab, bcbc, cdc, cda, dab, dda)

세번째 자리를 기준으로 정렬한다.

(abcd, acab, bcbc, cda, cdc, dab, dda)

Bit Manipulation

문제 제시 : 주어진 32비트 unsigned int에 1인 비트는 몇 개인가?
Hamming Weight
간단한 방법 : Bit mask를 통해서 shift하면서 한 비트씩 확인한다. 32*5
약간 멋있는 방법 : x와 x-1을 bitwise AND한다. 제일 오른쪽 한 비트가 사라짐.
010100100 & 010100011 = 010100000
0이 될 때 까지 반복횟수함.
이상한 방법 :

• 각 비트를 0/1인 숫자로 보자
• 두개식 쌍을 지어 더하는 것을 반복하자.
  $O(logN)$