Quick Sort

Merge sort

merge sort는 여러개의 자료를 한번에 정렬하지 않는다. 대신 먼저 작게 나누고, 나눈 자료들을 정렬하며, 정렬한 자료들을 재배치한다. $O(nlogn)$의 시간 복잡도를 가진다. 새로운 배열을 만들어야 한다는 점에서 공간이 많이 들고 어느 정도 정렬되어 있는 배열에 대해서도 거의 똑같은 시간이 걸린다는 점이 단점이다.

Quick Sort

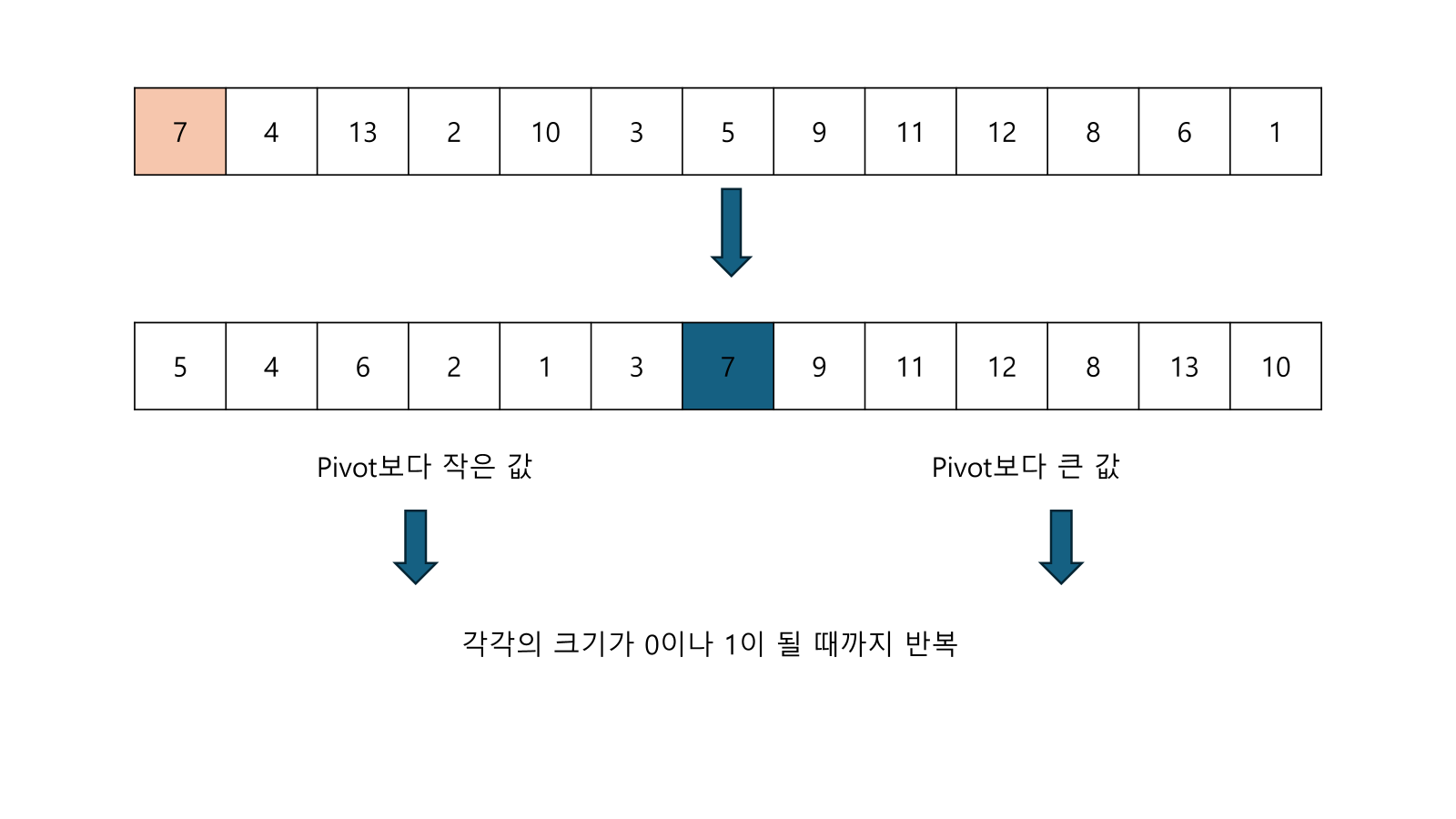
• 배열 안에 있는 한 요소를 선택한다. 이걸 피벗(pivot)이라고 한다.
• 피벗을 기준으로 피벗보다 작은 요소들은 왼쪽으로 옮기고 피벗보다 큰 요소들은 오른쪽으로 옮겨진다.
• 피벗을 제외한 왼쪽과 오른쪽을 다시 정렬한다
  • 왼쪽에서 피벗을 하나 뽑아서 정렬한다
  • 오른쪽에서 피벗을 하나 뽑아서 정렬한다
• 더 이상 분할이 되지 않을때까지 반복한다.
  

Worst Case : $O(n^2)$
Best Case : $O(nlogn)$
Average Case :

• $T(n) = \frac{1}{n} \sum_{k=1}^nT(k-1)+T(n-k) + n$
• $T(n) = \frac{2}{n} \sum_{k=1}^{n-1}T(k) + n$
• $T(n-1) = \frac{2}{n-1} \sum_{k=1}^{n-2}T(k) + n-1$
• $nT(n) = \sum_{k=1}^{n-1}T(k) + n^2$
• $(n-1)T(n-1) = \sum_{k=1}^{n-2}T(k) + (n-1)^2$
• $nT(n) = (n+1)T(n-1) + 2n-1$
• $\frac{T(n)}{n+1} = \frac{T(n-1)}{n} + \frac{2n-1}{n(n+1)}$
• $\frac{T(n)}{n+1} = \frac{T(n-1)}{n} + \frac{3}{n+1} - \frac{1}{n}$
• $\frac{T(n-1)}{n} = \frac{T(n-2)}{n-1} + \frac{3}{n} - \frac{1}{n-1}$
• $\frac{T(n)}{n+1} = \frac{3}{n+1} + 2\sum_{k=1}^{n}(\frac{1}{k}) - 1$

Selection Problem

• 퀵소트에서 제일 시간을 빠르게 하는 Pivot을 구할 수 있을까?
• $O(N)$개로 찾고, Best case인 $O(NlogN)$으로 정렬
• k번째를 찾아서 pivot으로 하기
  • Minimum, Maximum, Median, Selection
• 더 좋은 방법이 있을까?
• 배열을 나누기
• 똑같이 quick sort를 한 후에 한쪽만 내려가기(하나만 찾으면 되므로)

Approximate Median Problem

$rn$과 $(1-r)n$ 사이의 값
0 < r < 1일 때 r을 0.3으로 하면 약 40%가 포함됨
입력을 5개씩 나눔
나눈 입력들끼리 정렬함
등수끼리 묶음
3등 등수의 제일 가운데 값
그러면 가운데 값 보다 확실히 작은 애가 30% 있고, 확실히 큰 애가 30% 있으므로 3등 등수의 제일 가운데 값은 approximae median에 들어감

S(n) = A(n) + n + S(0.7n)
A(n) = n + S(0.2n)
S(n) = 2n + S(0.2n) + S(0.7n)
S(n) = O(n)
잘 쓰지는 않음. 많이 느림