Closest Pair

Closest Pair

• Computational Geometry
• 도형과 기하에 관한 문제들
• 직관과 심하게 충돌하는 경우 많음
• 주어진 점들 중에서 가장 가까운 쌍을 찾기 (2차원)
• 입력은 점들의 좌표들(Coordinates)로 주어짐
• $O(n^2) <-> O(n)$
• 아무리 빨라도 1차원보다 빠르지 못함. 왜냐하면 1차원을 포함하기 때문

1-Dimensional Version

• 먼저 하나의 값에 대해서 정렬(Sorting)함 $O(n)$
• 그 뒤 다른 모든 점과의 거리를 재서 가장 가까운 쌍을 찾음
• 같은 값이 있으면 제일 빨리 풀리기 때문에(값이 0이므로 가까운 쌍을 찾을 필요가 없다) 이 시간보다 오래걸림.
• $O(n^2)$

Divide and Conquer

• 먼저, x좌표를 기준으로 정렬한다. $O(nlogn)$
• 그 뒤, 왼쪽과 오른쪽으로 나눈다.
  • 왼쪽을 $DL$, 오른쪽을 $DR$이라고 하자.
  • $D = min(DL, DR)$라고 하자.
    
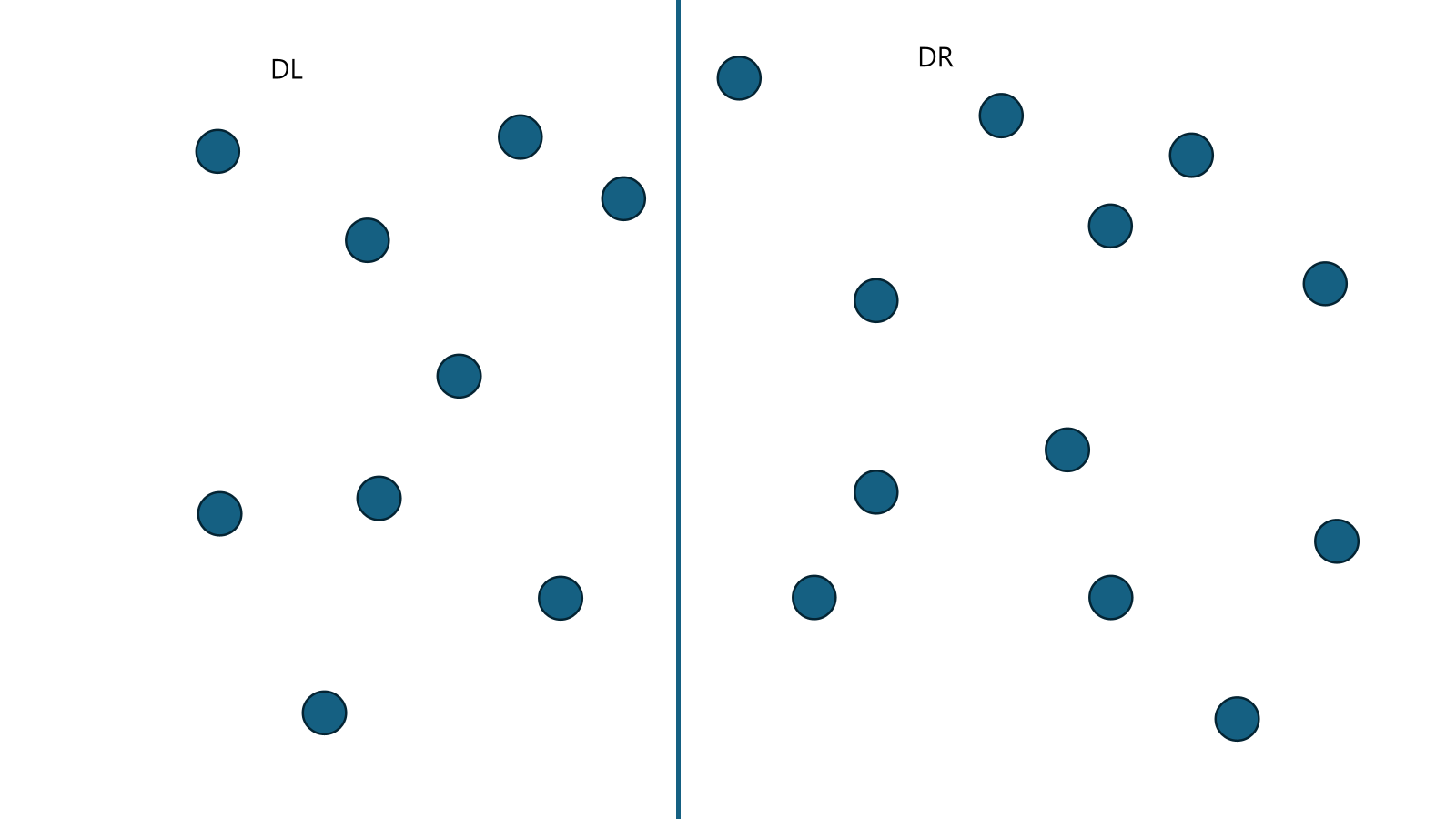
• 재귀를 사용한다.
• $DL$과 $DR$의 양쪽으로 각각 $D$의 거리만큼 공간을 준다. 이 공간을 Band라고 부른다.
  
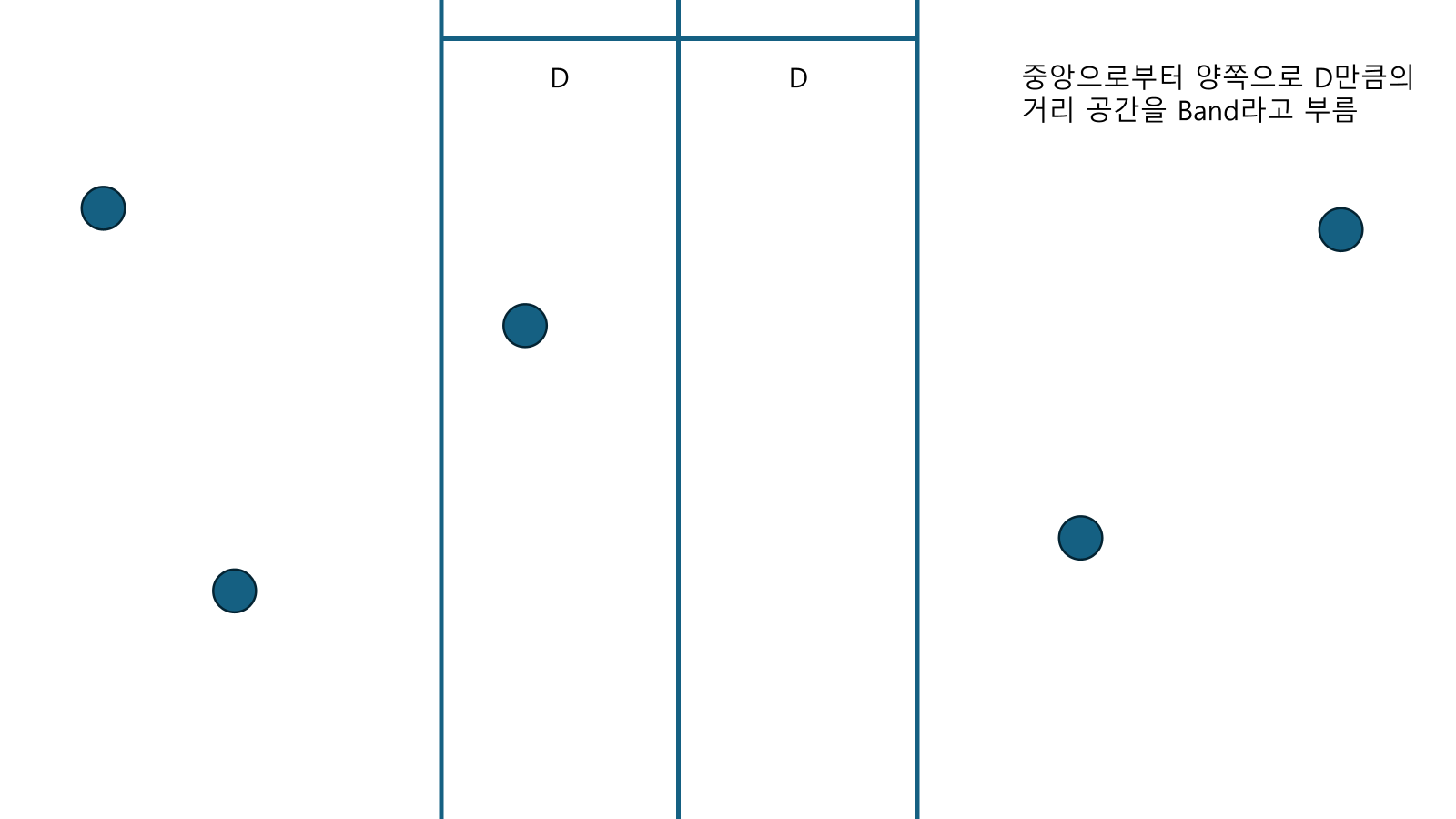
  • Band 밖의 애들은 이미 최소거리 $D$를 넘어섰기 때문에 고려할 필요가 없다.
  • 하지만 최악의 경우 모든 경우를 고려해야 함
• Key Difficulty
  • 점과 Band를 기준으로 $D$의 길이를 가진 정사각형 4개를 그려보자. 그러면 하나의 정사각형에는 최대 3개의 점이 들어갈 수 있다.
    
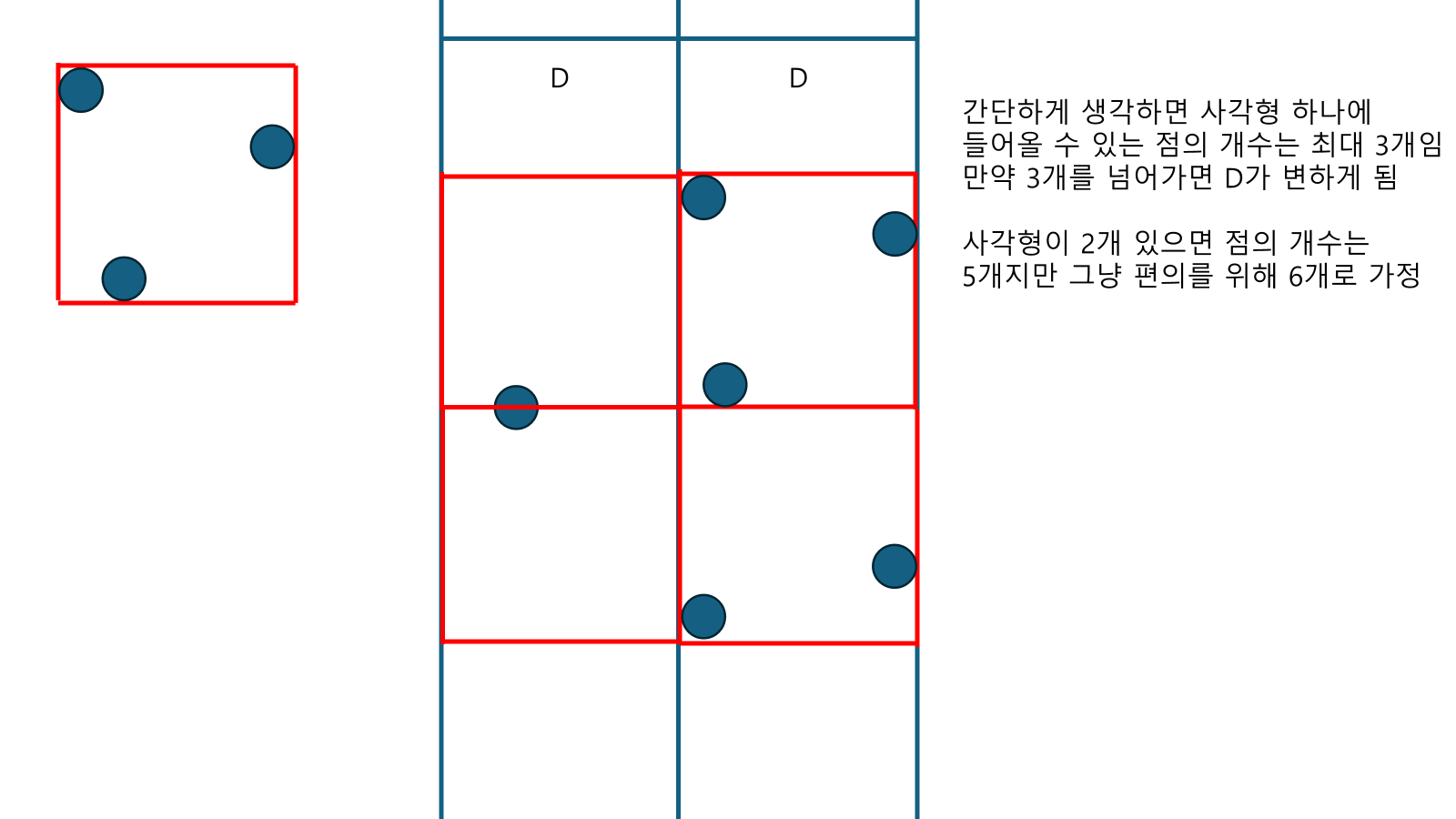
  • 다시 말해, D보다 길이가 작으려면 Band안에 있어야 하며, 2개의 사각형 안에 들어와야 한다는 소리이다.
  • 이 밴드에서 y좌표 기준으로 정렬하고, 자기 위의 6개의 점들과 거리를 확인한다.
    
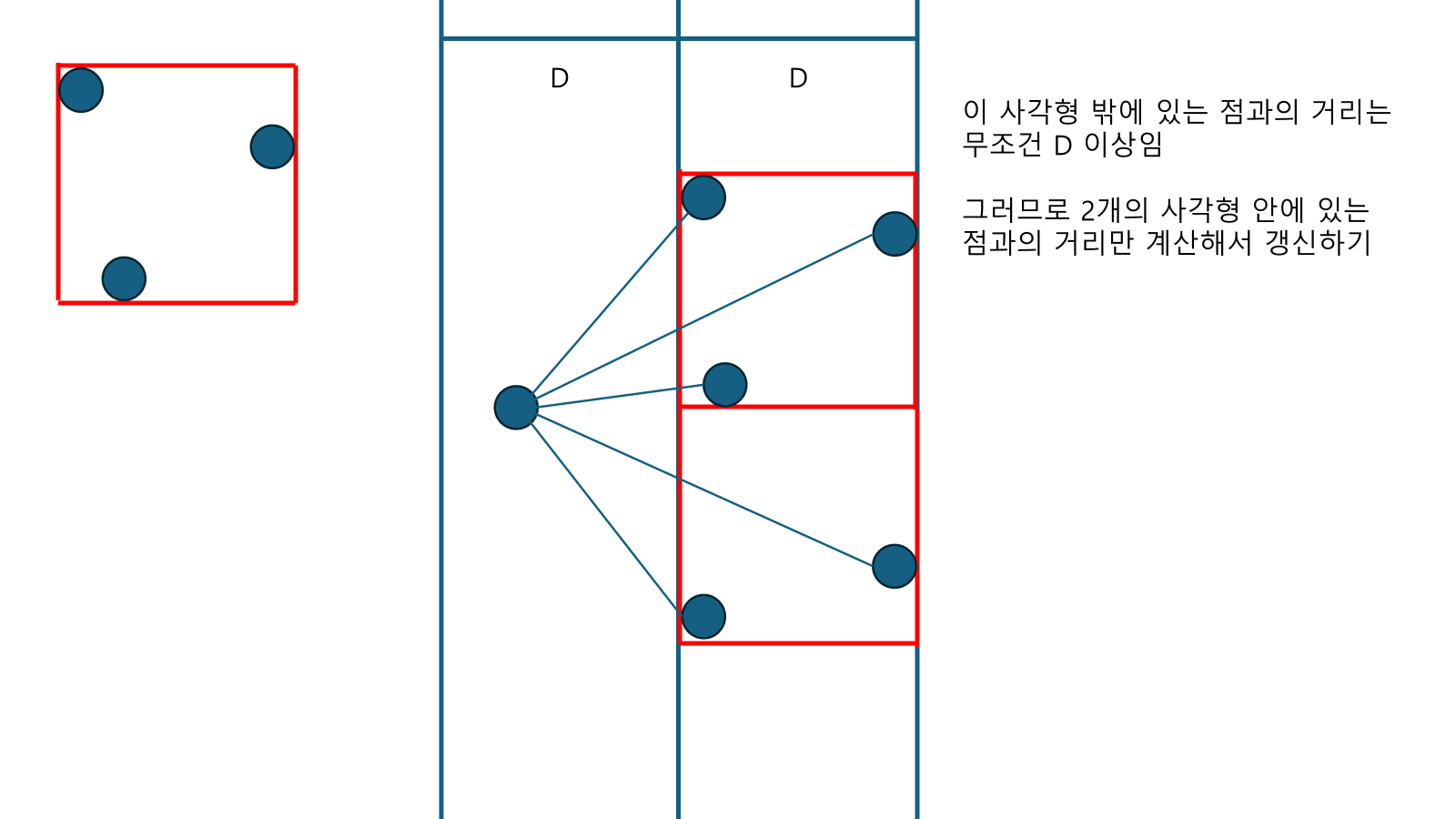
  • 반복한다.

각 과정에 대해 $O(nlogn)$만큼 걸리며 다시 합치는 과정에서 Band 기준으로 D를 다시 갱신하므로 $O(nlog^2n)$가 걸린다.

여기서 더 성능을 줄일 수 있음

• 모든 점을 x 기준으로 sort하기. $O(nlogn)$
• 재귀를 사용해서 작게 내려가면서 구함
  
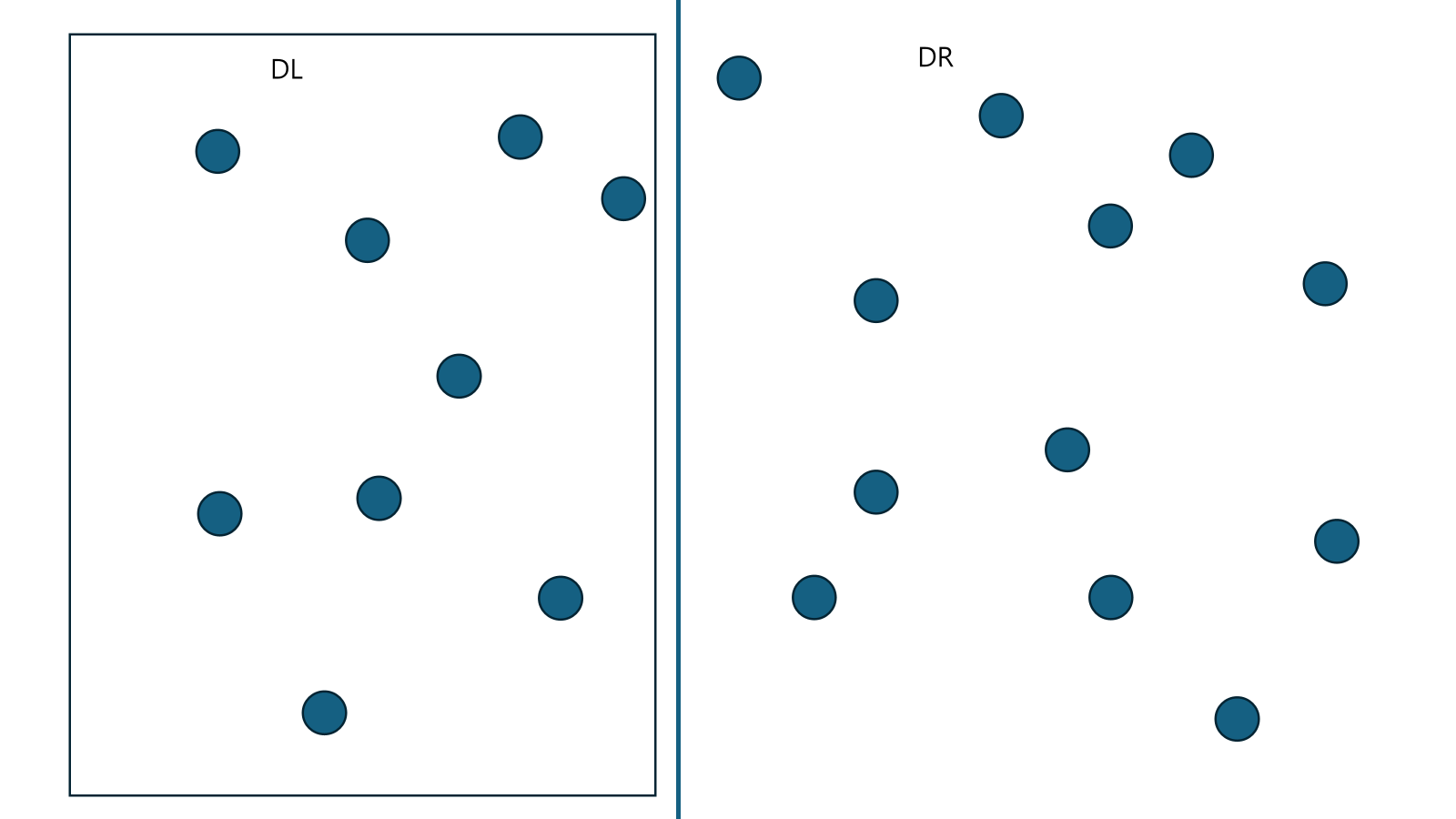
• $D = min(DL, DR)$을 구함.
• 모든 점을 y 기준으로 sort하기. $O(nlogn)$
• $D$를 구한 후 자신보다 위에 있는 6개의 점이 Band 안에 있는지를 확인함
• 자신보다 위에 있는 6개의 점 중 Band안에 있는 점과 거리를 비교하여 $D$를 갱신
  ![]
• 처음에 y 좌표에 대해 정렬했으므로 merge만 하면 알고리즘이 유지됨. $O(n)$

다시 말해 앞에서 divide를 했고 뒤에서 sort가 아닌 merge를 함으로써 merge sort의 성능을 낼 수 있음

$O(nlogn)$