아래 내용들은 컴퓨테이션 이론을 듣기 전 기본적으로 알고 있어야 할 지식들이다. 모르면 많이 힘들 가능성 존재
집합
-
집합(set)은 원소들을 나란히 놓아둔 것이다.
예시 : S : {7, 21, 57}
참고로 S : {21, 57, 7}랑 같다. 순서는 고려하지 않음 -
∈는 집합 안에 원소가 존재한다는 기호, ∉는 원소가 존재하지 않는다는 기호다. 7 ∈{7, 21, 57}, 8∉{7, 21, 57}
-
⊆는 부분집합(subset) 기호, ⊂는 진부분집합(proper subset) 기호이다. 어떤 집합의 모든 원소가 다른 집합 안에 있으면 부분집합이라고 하고, 여기서 자기 자신을 제외한 부분집합을 진부분집합이라고 한다.
-
multiset은 {7} 이랑 {7,7}을 다르게 표기하고 싶을 때 사용한다. 어떤 문제를 풀 때는 7이 한개인지 두개인지를 다르게 해야 할 때가 생기므로 그럴 때 사용한다.
-
무한집합(infinite set)은 원소 개수가 무한이 많은 집합을 말한다.
-
공집합(empty set)은 원소 수가 없는 집합을 말하며, 기호는 ∅이다.
-
합집합(union)은 A와 B의 모든 원소를 포함한 집합, 교집합(intersection)은 A와 B가 같이 가지고 있는 모든 원소를 포함한 집합, 여집합(complement)은 A의 원소를 제외한 모든 원소를 포함한 집합을 의미한다.
-
Venn diagram(벤 다이어그램)은 집합을 시각화한 것이다.
시퀀스와 튜플
-
시퀀스(Sequence)는 순서가 중요할 때 나타내는 방법이며, (7, 21, 57) 와
(21, 57, 7)은 다르다. 또한 (7, 7, 21, 57)과도 다르다. 집합은 모두 같은것과 비교된다. -
Finite sequence는 보통 튜플(tuple)이라고 부르며, k개의 원소를 가진 시퀀스를 k-tuple이라고 한다. 2-tuple은 ordered pair라고 부르기도 한다. ( , )형태의 순서가 중요한 시퀀스를 의미함.
-
power set은 집합의 원소들을 부분집합으로 가지는 모든 집합을 말한다. 예를 들어 S={1,2,3}일 때, power set은 2^s = {{∅},{1},{2},{3},{1,2},{1,3},{2,3}{1,2,3}}이다.
-
멱집합(Cartesian product or cross product)은 집합 A와 B가 있을 때, A를 첫번째 원소로 가지고, B를 두번째 원소로 가지는 집합이다. A X B로 표기한다. 예를 들어 A = {1,2}, B = {x,y,z} 면 A X B = {(1,x),(1,y),(1,z),(2,x),(2,y),(2,z)}... 참고로 멱집합은 여러개가 가능한데, 예를 들어 A X B X A면 (1,x,1), (1,x,2) ... 이렇게 가지게 된다.
함수와 관계
-
함수는 f(a) = b로 나타내며, input을 넣어서 output이 나오는 것을 의미한다. mapping이라고도 불린다.
-
함수의 input들을 정의역(domain)이라고 하며, outcome을 공역(range)이라고 한다. 그래서 함수를 f : D -> R 이라고 할 수 있으며, domain에서 range로 보내는 것이 함수이다.
-
함수 f의 정의역이 A1 X ... X Ak면, f에 들어가는 input들은 k-tuple(a1, a2, ..., ak)이다. 여기서 우리는 input 각각의 하나하나를 매개변수(argument)라고 한다. f(a1, a2, ..., ak)같은 k개의 매개변수를 가지는 함수를 k-ary function이라고 하며, k는 항수(arity)라고 한다.
-
1개의 매개변수는 unary function, 2개면 binary function이라고 하며, 0개면 nullary function이라고 한다.
-
함수의 공역이 {TRUE, FALSE}면 predicate 또는 property라고 한다. 공역이 k-tuple인 property를 relation이라고 하고, k-ary relation 이라고 부르기도 한다. 대부분 공역의 튜플이 2개 이상의 쌍을 가지는 property를 말할때 쓰인다.
Example
가위바위보의 예시

| 아래가 옆이랑 붙어서 이기는가? | Scissors | Paper | Rock |
|---|---|---|---|
| Scissors | FALSE | TRUE | FALSE |
| Paper | FALSE | FALSE | TRUE |
| Rock | TRUE | FALSE | FALSE |
이런 경우의 수들을 모두 나타내려면 복잡함. (S,P) = T / (S,S) = F ..... 이런 식으로 9개를 작성해야 하는데, 만약 경우의 수가 많아지면?
그래서 predicate는 P : D -> {TRUE, FALSE} 를 (D,S)로 나타낼 수 있는데, S = {a ∈ D | P(a) = true}이다. 다시말해 D는 predicate를 TRUE로 만드는 D를 모아둔 집합이며, D가 말하는 것이 명확할 경우 생략해서 나타낼 수 있다. 그러므로 앞 예시를 {(S,P), (P,R) (R,S)} 이렇게 나타낼 수 있다.
Graph
-
무방향 그래프, 쉽게 말해 그래프는 포인트(노드)들과 포인트(노드)들을 연결하는 선들의 집합이다. 이 포인트들을 node나 vertices라고 부르며, 선들을 edge라고 부른다.
-
node에 연결되어 있는 선의 개수를 degree라고 말한다.
-
그래프 G에서 node i와 node j를 연결하는 선을 (i,j)로 표기한다. V를 그래프의 node라고 하고, E를 edge라고 하면 그래프 G는 G = (V,E)로 표기 될 수 있다.
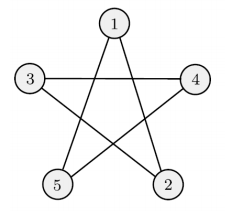
이 그래프는 ({1, 2, 3, 4, 5}, {(1, 2),(2, 3),(3, 4),(4, 5),(5, 1)})로 나타낼 수 있음. -
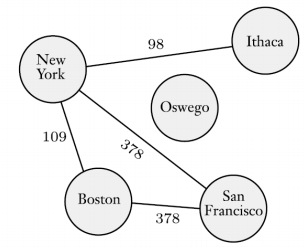
그래프의 node나 edge에 표시를 할 수도 있으며, 이렇게 이름을 붙힌 것을 labeled graph라고 부른다.
-
G = {V', E'}이고, H = {V,E}일 때, V'는 V의 부분집합이고, E'는 E의 부분집합일때 G는 H의 subgraph라고 한다.
-
path는 node 사이를 연결하는 sequence를 의미한다. 여기서 node 사이에 edge가 없는데 path에서 연결하려고 하면 그것은 path가 아니다.
-
simple path는 한 번 나온 node가 다시 등장하지 않는 path를 말하며, 다시 말해 cycle이 없는 노드다.
-
모든 node를 연결하는 path가 있으면 그래프가 connected되었다고 말한다.
-
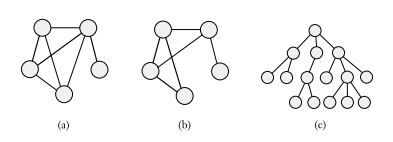
같은 node에서 시작해서 같은 node에서 끝나면 cycle이라고 하며, simple cycle은 적어도 node를 3개를 가지고 같은 node는 처음과 끝만 가능한 노드를 말한다.(한붓그리기) 그래프가 cycle이 없으면 tree라고 한다.
-
만약 edge에 방향성이 있으면(선 대신 화살표) directed graph(방향 그래프)라고 부른다. 각각의 node에 들어오는 degree중 들어오는 것을 indegree, 나가는 것을 outdegree라고 한다. 이 그래프에서 path는 directed path라고 부른다. 방향성이 없는 그래프에서는 모든 node를 연결하는 path가 있으면 connected라고 했지만, 방향성이 있는 그래프에서는 서로를 모두 연결하는(각각이 연결되어 있는) 그래프에 대해서 strongly connected라고 말한다.