컴퓨테이션 이론

컴퓨테이션 이론에 대한 개론

본론으로 들어가기 전 1930년도에 세워졌던 새가지 이론을 짚고 넘어가자

아래 내용들은 컴퓨테이션 이론을 듣기 전 기본적으로 알고 있어야 할 지식들이다. 모르면 많이 힘들 가능성 존재 집합 집합(set)은 원소들을 나란히 놓아둔 것이다. 예시 : S : {7, 21, 57} 참고로 S : {21, 57, 7}랑 같다. 순서는 고려하지 않음 ∈는 집합 안에 원소가 존재한다는 기호, ∉는 원소가 존재하지 않는다는 기호다. 7 ∈...

문자열(String)과 언어(Language)에 대한 컴퓨터 공학적인 접근

Boolean Logic >불 논리는 TRUE나 FALSE, 또는 1과 0으로 나타내는 논리를 말한다.

컴퓨터가 무엇인가? "컴퓨터가 무엇인가?" 라고 하면 한마디로 정의하기엔 힘들 것이다. PC나 노트북, 핸드폰등은 컴퓨터인가? 그럴 것이다. 펜이나 전등은 컴퓨터라고 할 수 없을 것이다. 그렇다면 리모컨은? 인터폰은? 좁은 의미의 컴퓨터는 소프트웨어와 하드웨어로 구성

유한 오토마타가 하는 일 유한 오토마타가 하는 일을 수학적으로 나타낸다. M = (Q, Σ, δ, q0, F)이 주어지고, $w = w{1}w{2} · · · w{n}$을 심볼으로 가지는 알파벳 Σ가 있다. Q를 참조하는 시퀀스 $r{0}, r{1}, . . . , r{n}$ 들이 다음의 조건을 만족할 때 M은 w를 recognize한다. > $r0 ...

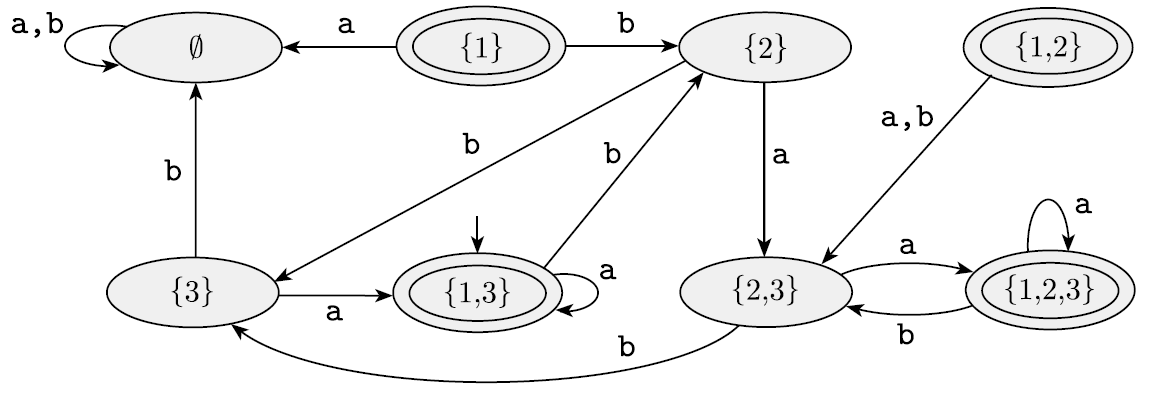
Nondeterminism과 NFA, 그리고 NFA == DFA

Union, Concatenantion, 그리고 Star

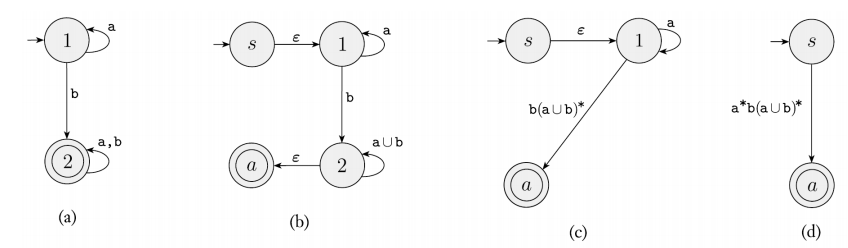
Generalized nondeterministic finite automata (GNFA)는 보통의 NFA와는 달리 regular expression을 transition arrow의 label로 가지는 NFA다.

language에서 regular operation을 통해서 식을 만들 수 있으며, 그 식을 regular expression이라고 부른다.

The Pumping Lemma for Regular Languages pumping lemma는 모든 regular language는 만족하지만 아니라면 만족하지 않는 lemma(정리)를 의미한다. pumping lemma를 통해 language가 P.L을 통과하지

유한 기계가 할 수 없는 일들에 대해서 알아보자.

우리는 context-free grammar를 배운다. 이건 우리가 지금까지 배운 것 보다 더욱 강력한 모델이다.

Pushdown Automata 우리가 새로운 language를 배웠으므로 이에 상응하는 새로운 컴퓨터의 모델이 나온다. Context-Free language를 나타내는 Automata가 바로 Pushdown Automata다. Pushdown Automata는 NF

Non-Context-Free Languages Regular Language를 공부할 때, Regular Language에 속하지 않는 Language도 공부하였다. 이와 비슷하게, Context-Free Language를 공부했으면, Context-Free Language에 속하지 않는 Language도 알아야 한다. Regular language의 p...

Turing Machines

Variants of Turing Machine

Definition of Algorithm

풀 수 없는 문제

Undecidability

Time Complexity in Computation Theory