동전 거스름돈과 LIS

동전 거스름 돈

• N원의 거스름 돈을 돌려주야 한다.
• $M_{500}, M_{100},...,M_{k}$등의 동전들이 있으며, 각각 가격은 500, 100, 등등 이다. 동전들의 종류는 각각 다르다.
• 최소 개수의 동전을 사용하여 거스름 돈을 돌려주는 방법을 구하여라
• 예를 들어 1원, 4원, 6원 동전 $M_1, M_4,M_6$이 무한히 있다.
• 8원을 거슬러 줘야 하면 어떻게 해야 하는가?
  • Greedy : 6/1/1 = 8로 3개
  • 최적의 방법 : 4/4 = 8로 2개
• 그리디로는 구하기 어려우며 동적 계획법으로 구해야 함

Pseudo polynomial

• $N$개의 값을 Sorting하는데 주어진 시간은 $O(NlogN)$
• 그러나 각각의 값에 따라서 Sorting하는 시간을 세세하게 달라짐
  • 예를 들어, 1bit값끼리 Sorting하는 것과 8bit값끼리 Sorting 하는 것은 시간 차이가 많이 남
• 그러므로 실제 시간은 $O(NlogNlog(maxδ_i))$
• $N = 2^{logN}$

해결법

• 모든 금액에 대해서 그 금액에 줄 수 있는 최소 개수를 적어놈
• $C[i] = i$원을 거슬러 준다고 할 때 $M_1, M_4,M_6$에 대해서 8원을 걸러주는 DP는 다음과 같다.
  • $C[0] = 0$
  • $C[1] = C[0] + 1 = 0 + 1 = 1$
  • $C[2] = C[1] + 1 = 1 + 1 = 2$
  • $C[3] = C[2] + 1 = 2 + 1 = 3$
  • $C[4] = min(C[3] + 1, C[0] + 1) + 1 = 0 + 1 = 1$
  • $C[5] = min(C[4] + 1, C[1] + 1) + 1 = 1 + 1 = 2$
  • $C[6] = min(C[5] + 1, C[2] + 1, C[0] + 1) + 1 = 0 + 1 = 1$
  • $C[7] = min(C[6] + 1, C[3] + 1, C[1] + 1) + 1= 1 + 1 = 2$
  • $C[8] = min(C[7] + 1, C[4] + 1, C[2] + 1) + 1= 1 + 1 = 2$
    

Longest Increasing Subsequence

• 원소가 n개인 배열이 있다.
• 이 배열을 substring을 뽑는다.
• substring중 각 원소가 이전 원소보다 크다는 조건을 만족하고, 그 길이가 최대인 부분 수열을 최장 증가 부분 수열(LIS)라고 한다.
• 이 때 서로 연결되어 있을 필요는 없다.
• $N^2$는 DP를 안다면 쉽다.

$N^2$ 해결법

• 새로운 배열 $S$를 하나 만든다. 이 배열은 $i$번째 값을 마지막으로 가지는 LIS의 최대 길이를 저장한다.
• 모든 $S[i]$에 대해서 0 ~ i-1 값까지를 보면서 어디에 붙을 수 있는지 확인하고, 가장 큰 값을 적는다.
• {3,10,4,7,5,1,6,8,9,2}에 대한 예시이다.
  
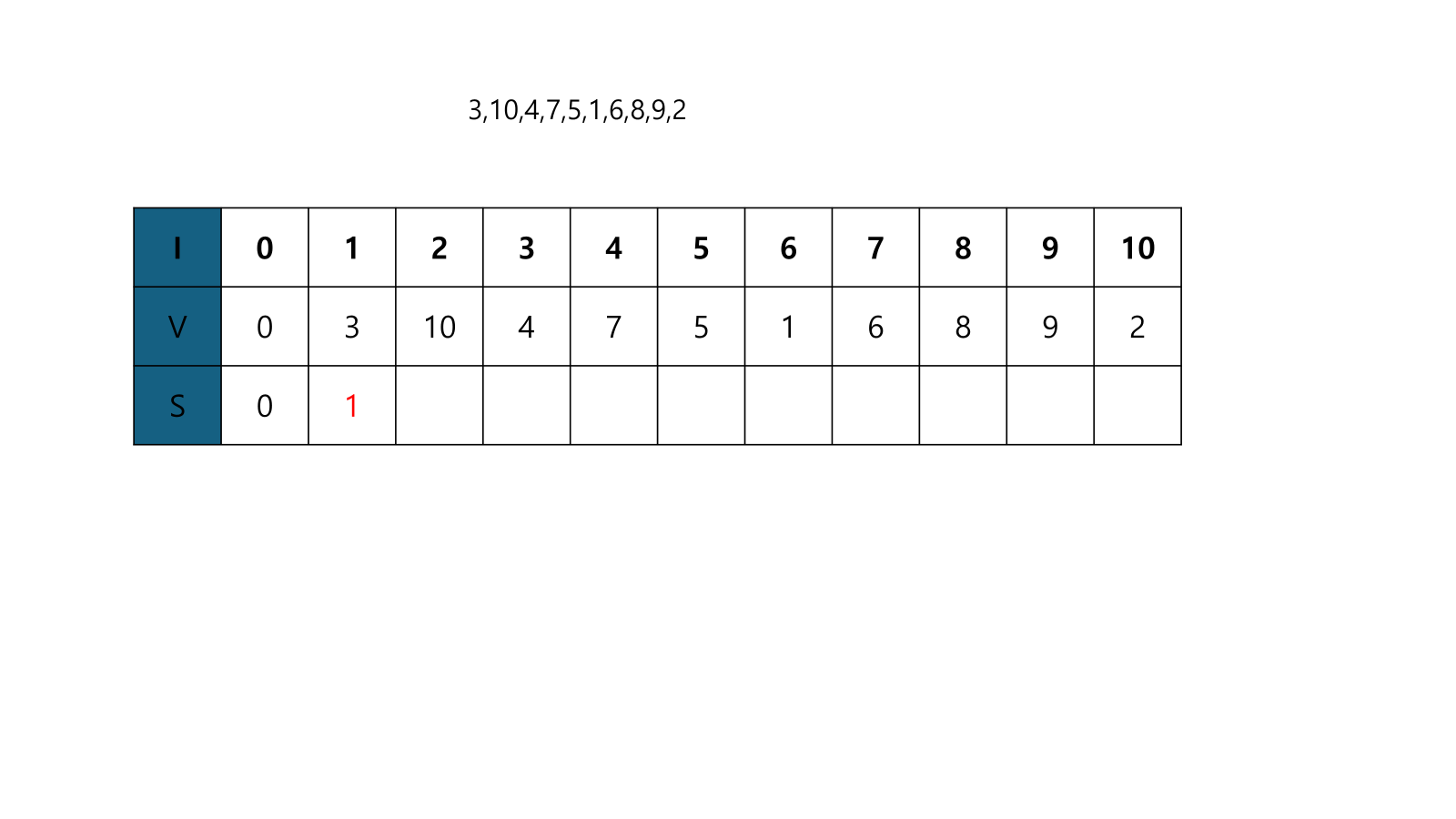
• 먼저 배열 $S$를 만든다. 처음을 0으로 초기화해준다.
  
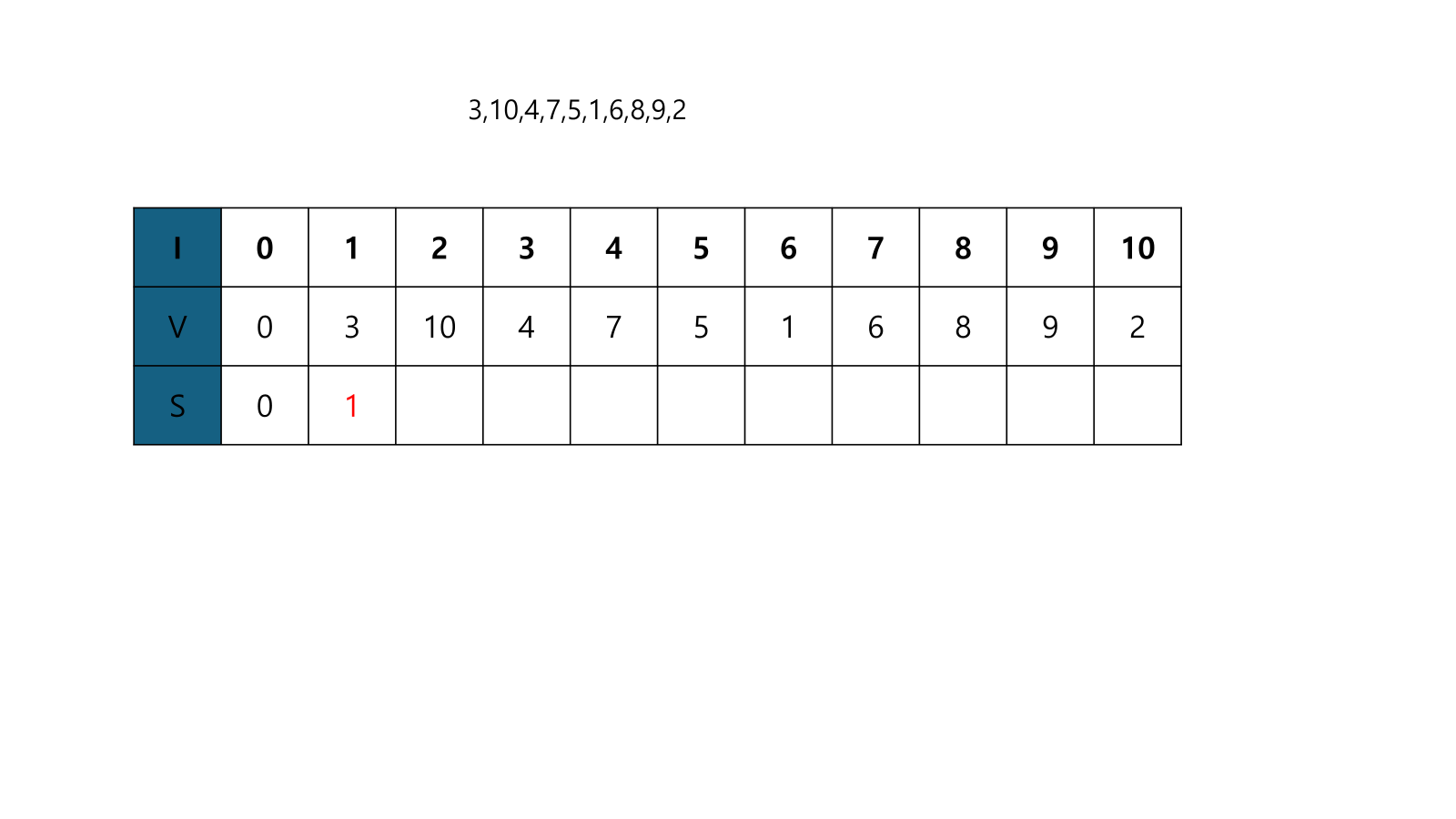
• 첫번째부터 확인한다. 3이 마지막일때 만들 수 있는 LIS의 길이는 1이므로, $S[1] = 1$이다.
  
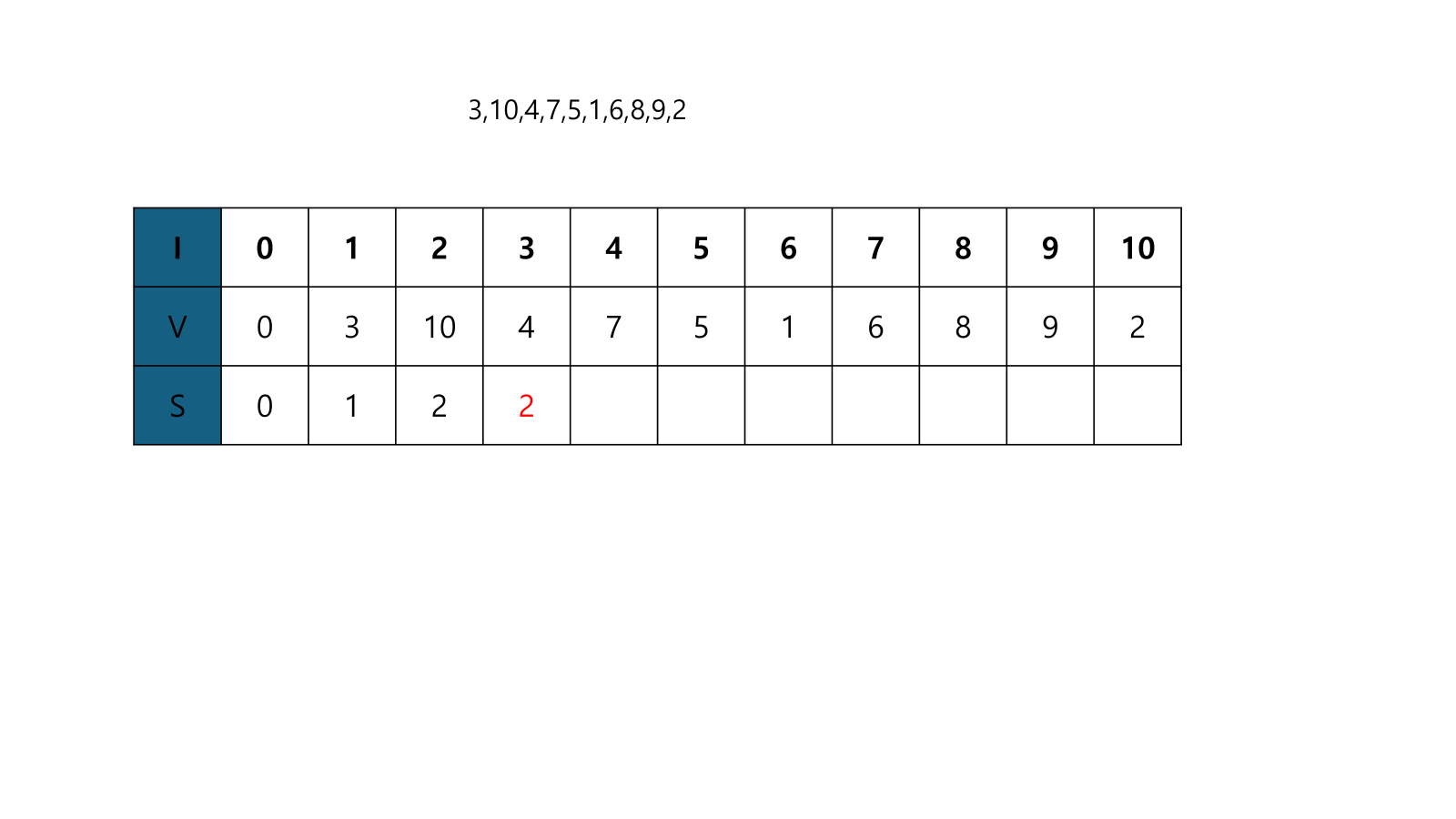
• $i=3$인 경우이다. 4가 마지막일 때 $V[j] < V[i]$인 j는 첫번째이며, $S[1] = 1$이므로 $S[3] = 2$이다.
  
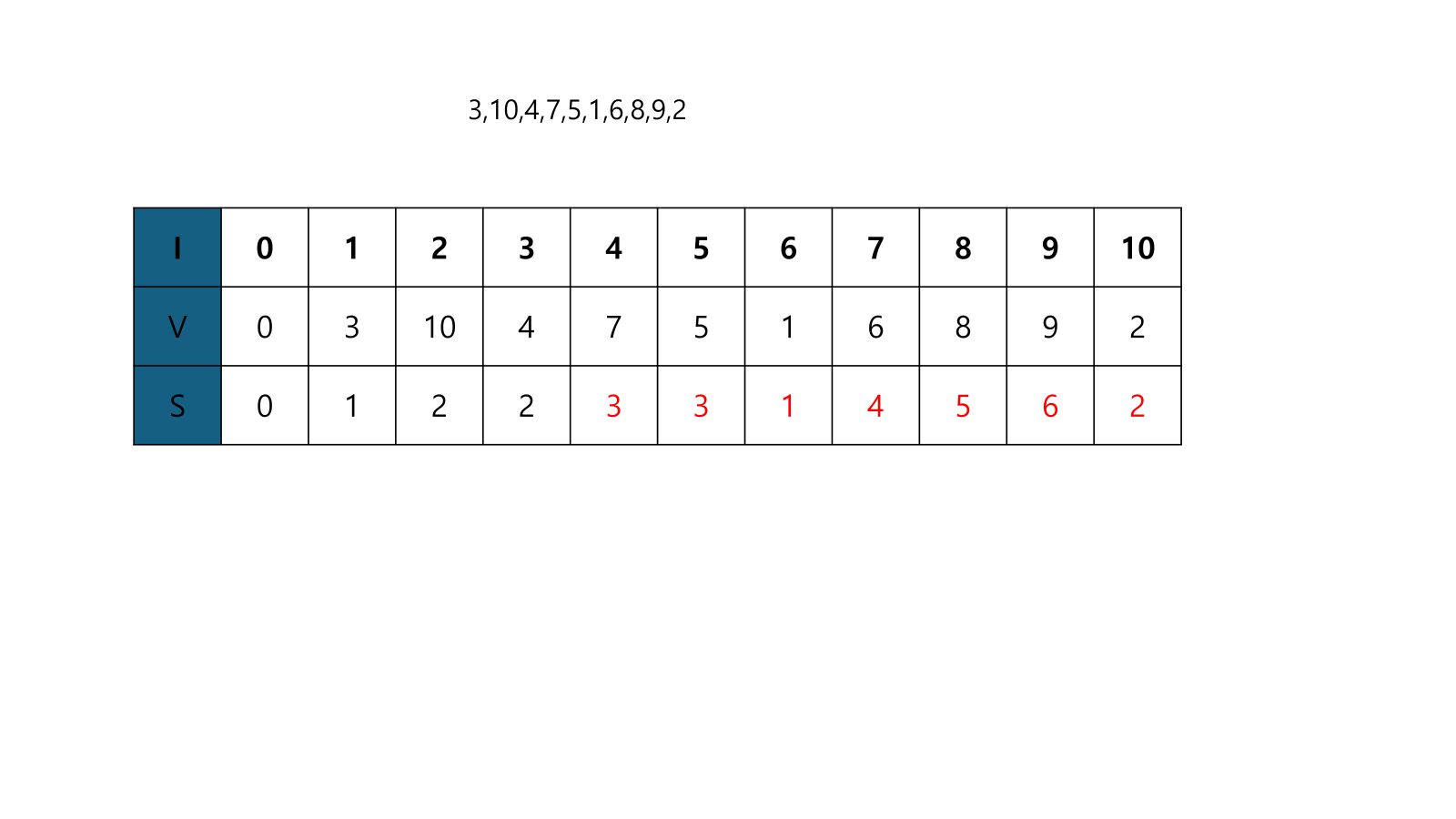
• 나머지도 같은 과정에 따라 채워준다.

$NlogN$ 해결법

• 만약 만들 수 있는 배열의 길이는 같은데, 값이 다른 두 숫자가 있다면, 무엇을 택해야 하는가?
• 예를 들어, {2,5,9}와, {2,5,7}중 더 길게 배열을 만들 수 있는 가능성이 높은 것은 무엇인가?
• 답은, {2,5,7}이다. 이후에 8/9가 나오면 앞에는 추가를 못하지만, 뒤에는 추가할 수 있다.
• 이러한 성질을 활용해서, $S$를 만들 때 사용한 제일 작은 값을 저장하는 배열 $A$를 또 만들어서, 시간을 $NlogN$으로 줄일 수 있다.
  
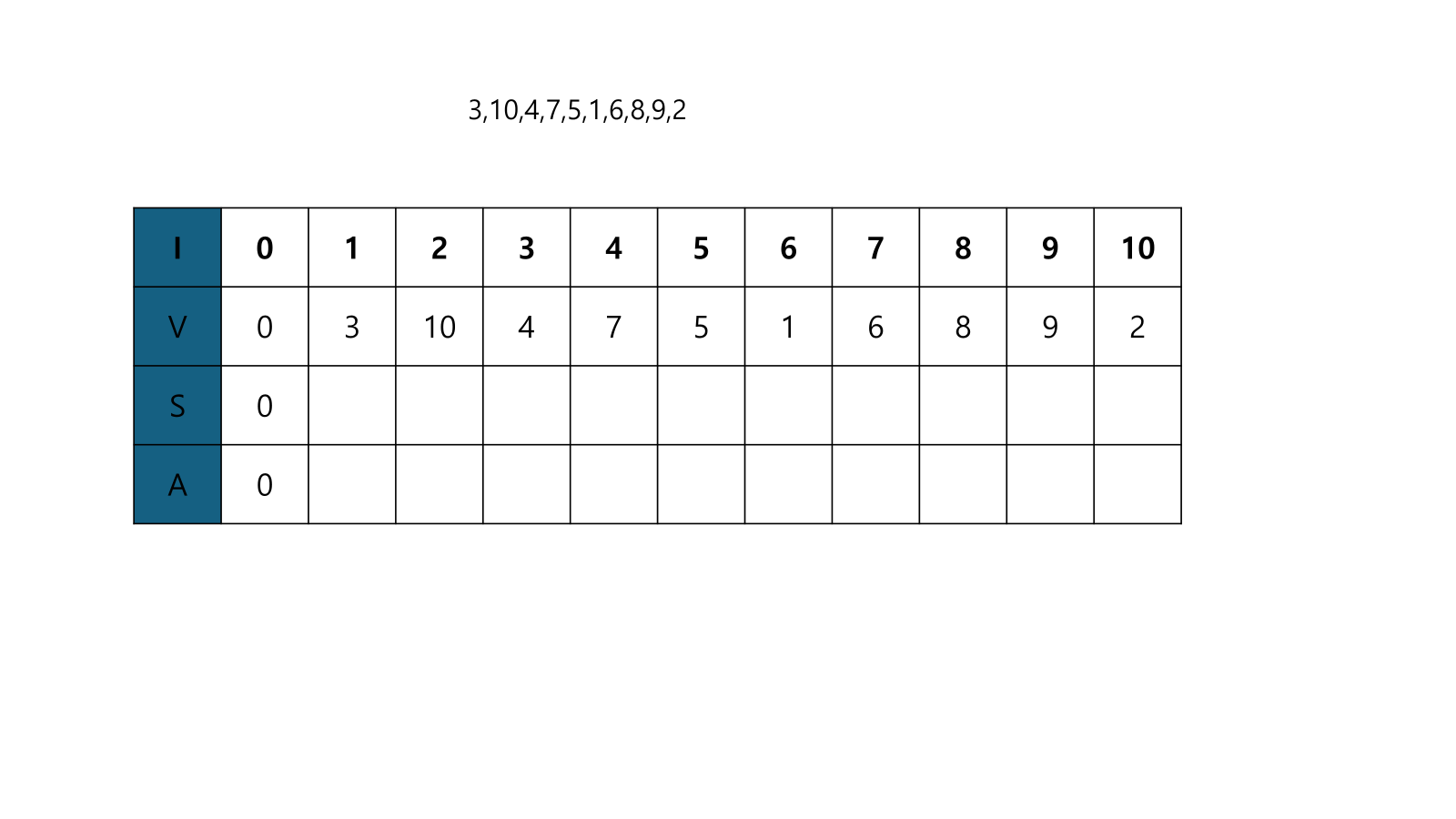
• 기존 방식에 $A$를 추가한다.
  
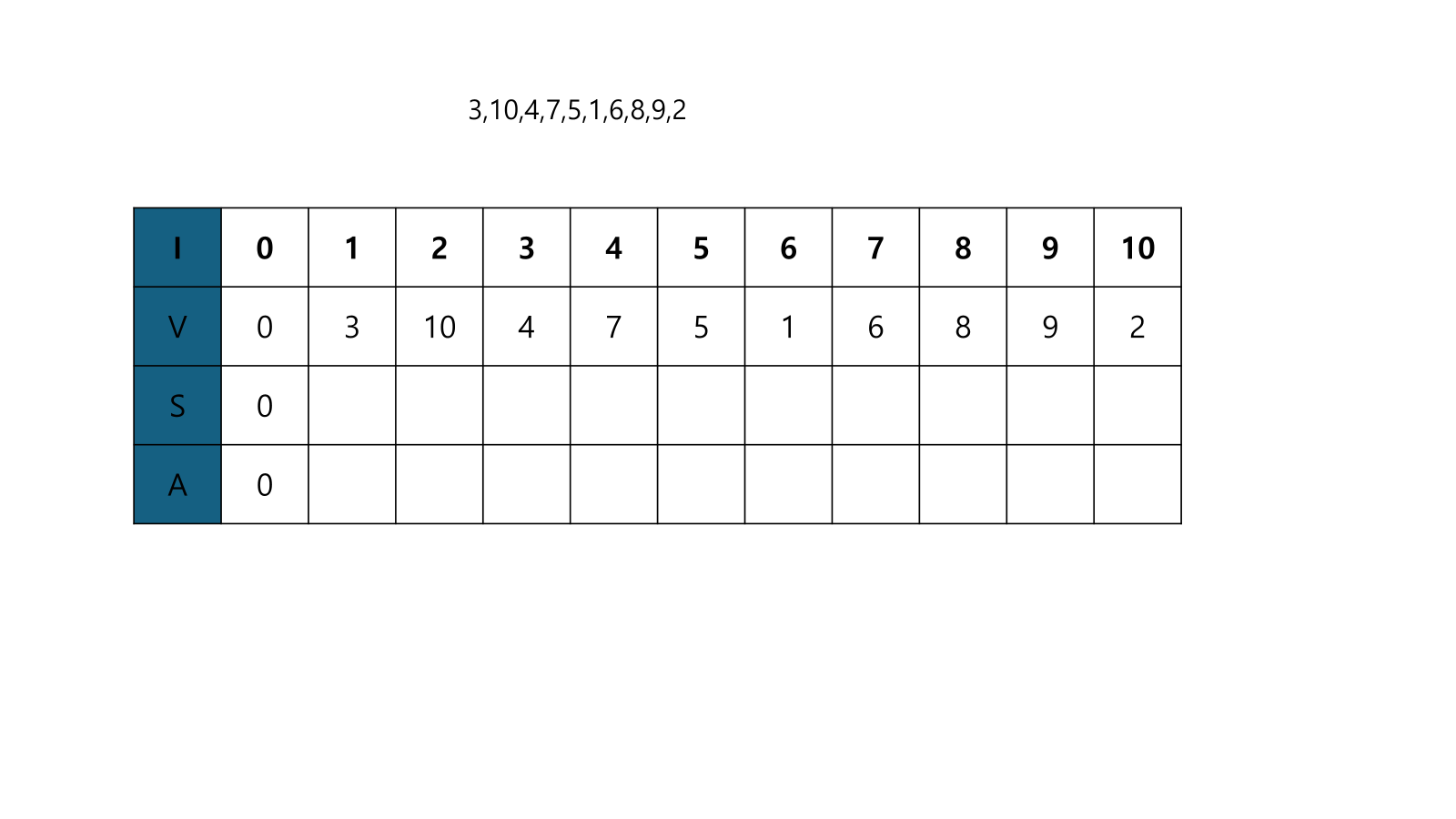
• $V[1]$은 $A[0] < V[1]$ 이므로, $A[1] = V[1]$
  
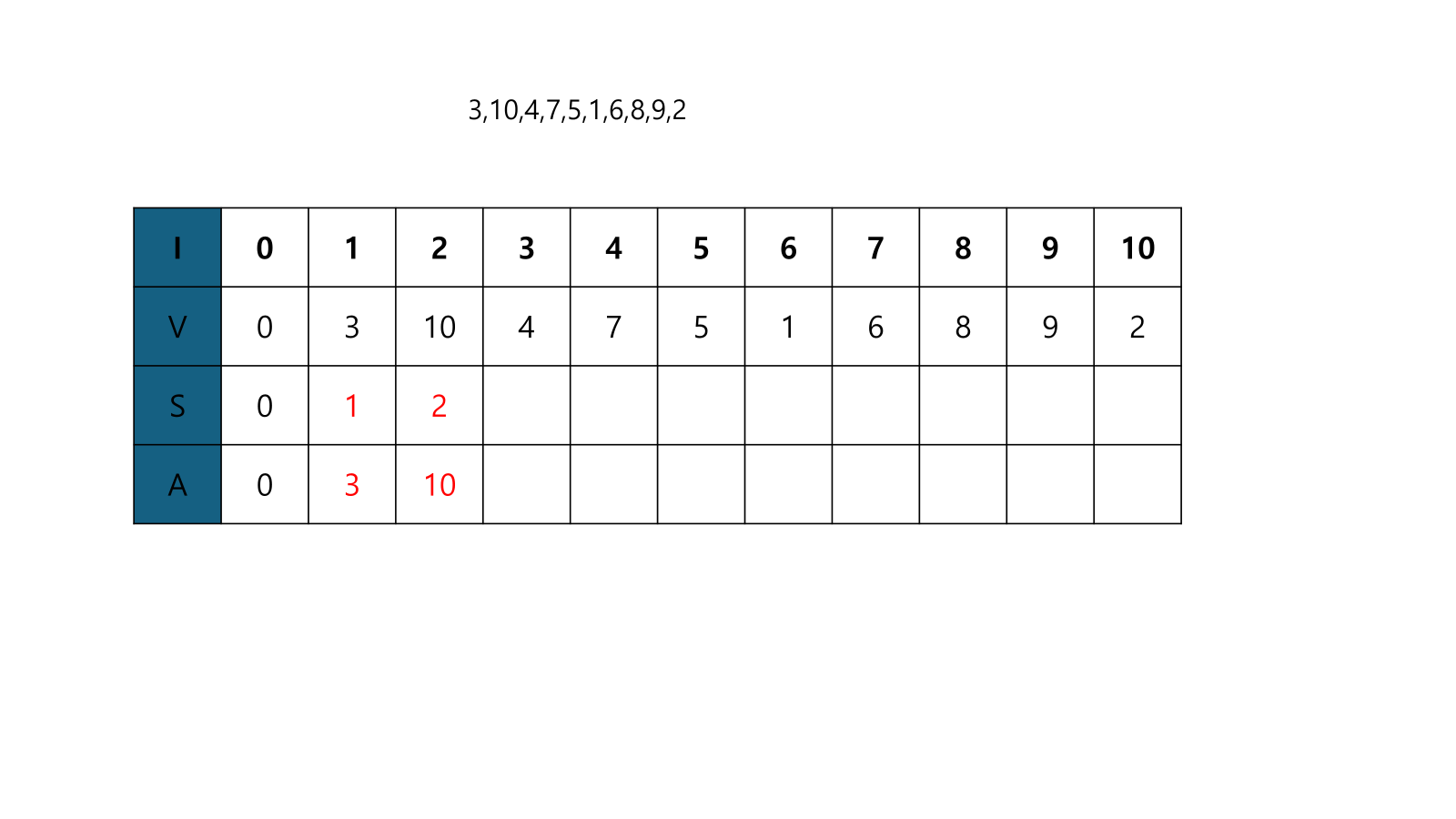
• $V[2]$은 $A[1] < V[2]$ 이므로, $A[2] = V[2]$
  
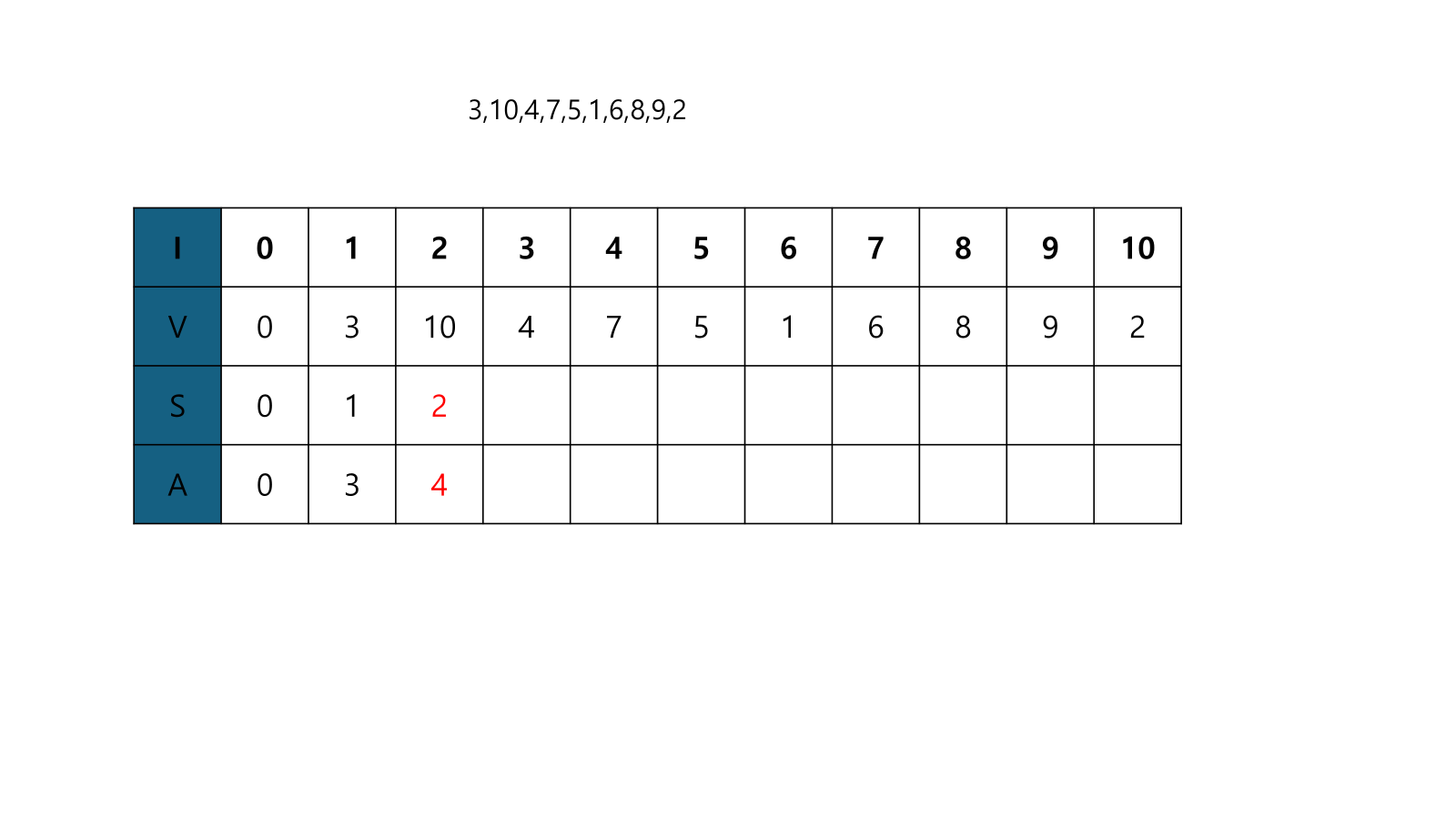
• $V[3]$은 $A[1] < V[3] < A[2]$이므로, $A[2]$를 $V[3]$으로 교체한다.
  
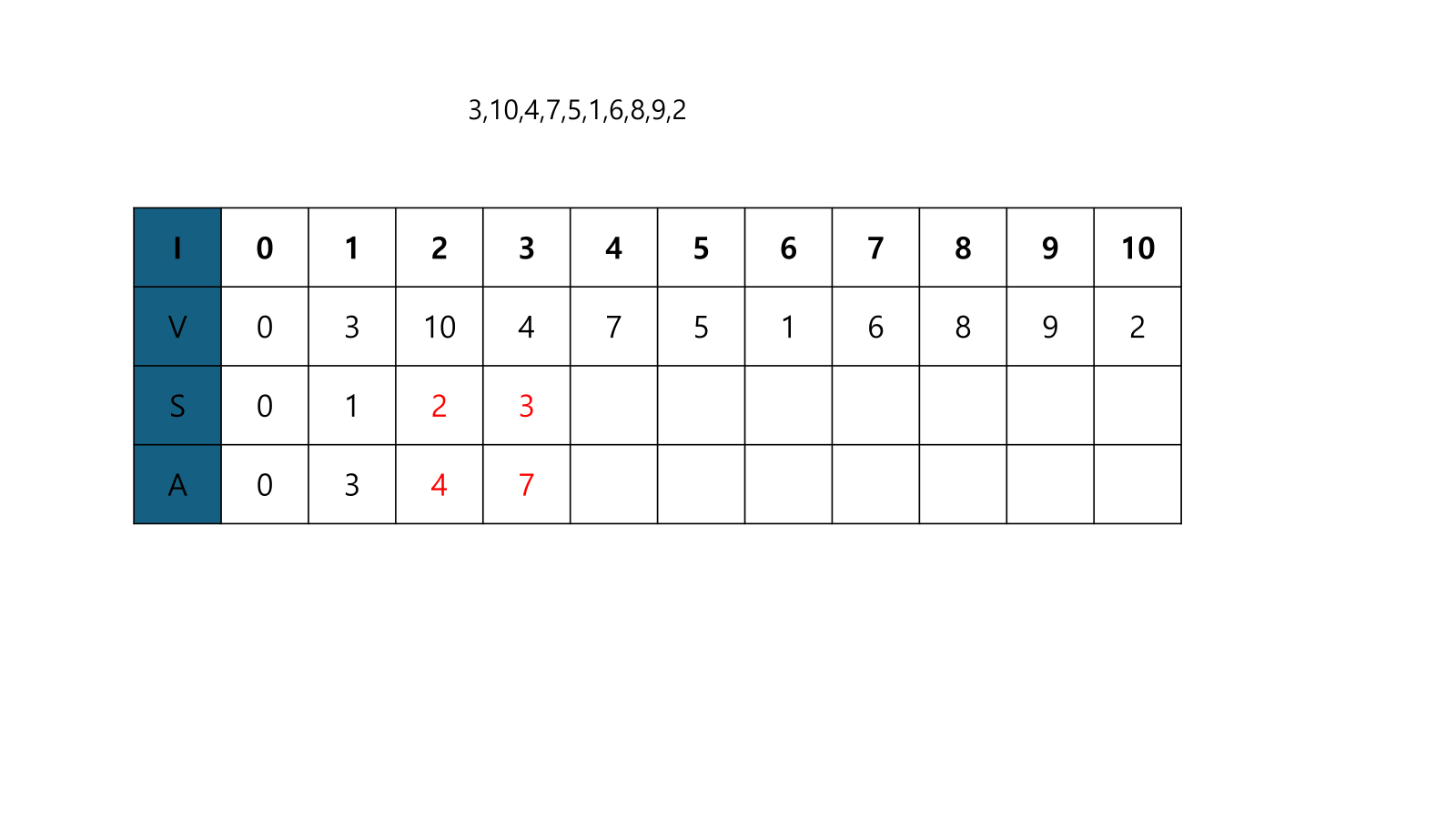
• $V[4]$은 $A[2] < V[4]$이므로, $A[3]=V[4]$
  
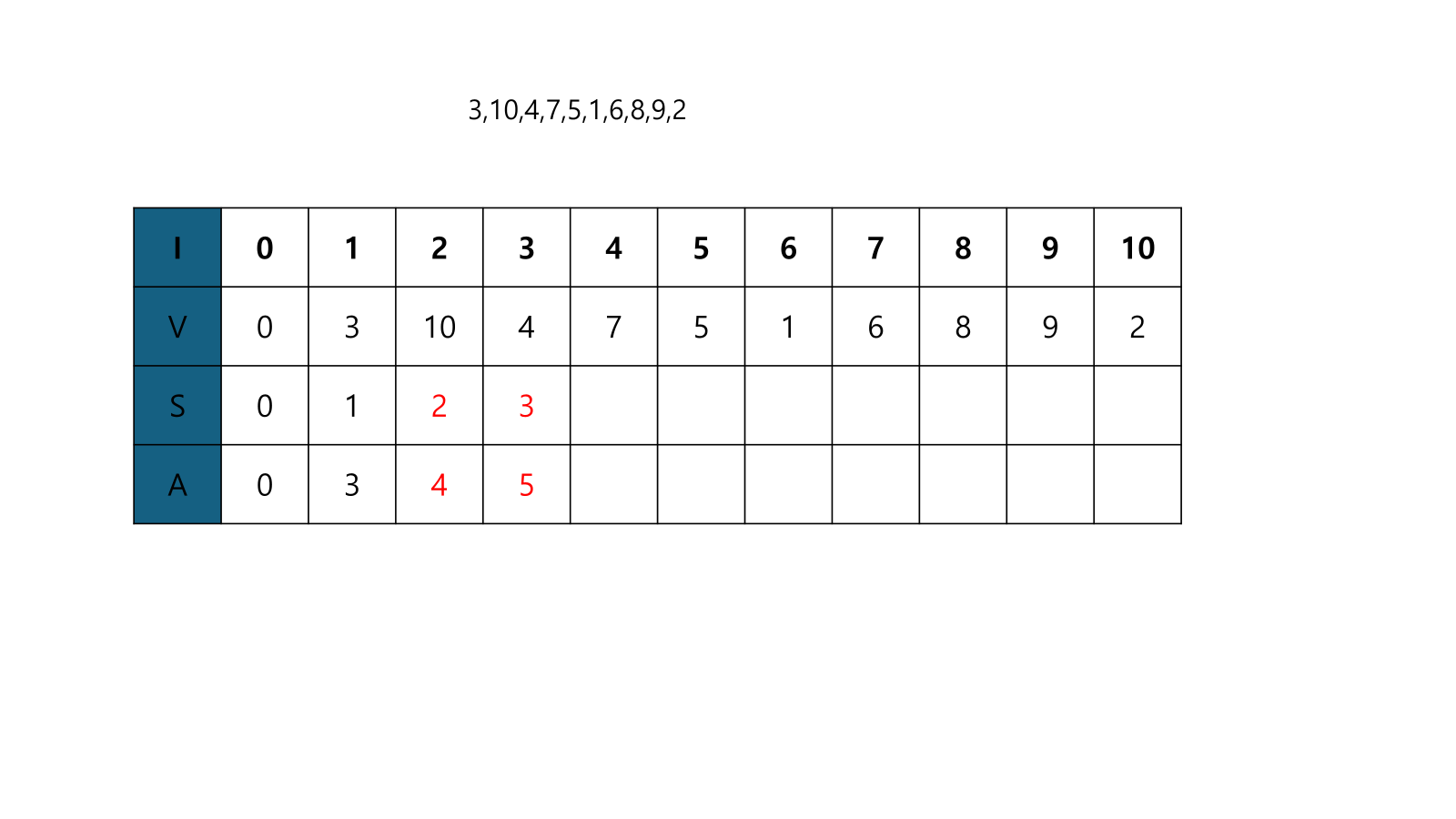
• $V[5]$은 $A[2] < V[5] < A[3]$이므로, $A[3]$을 V[5]$로 교체한다.
  
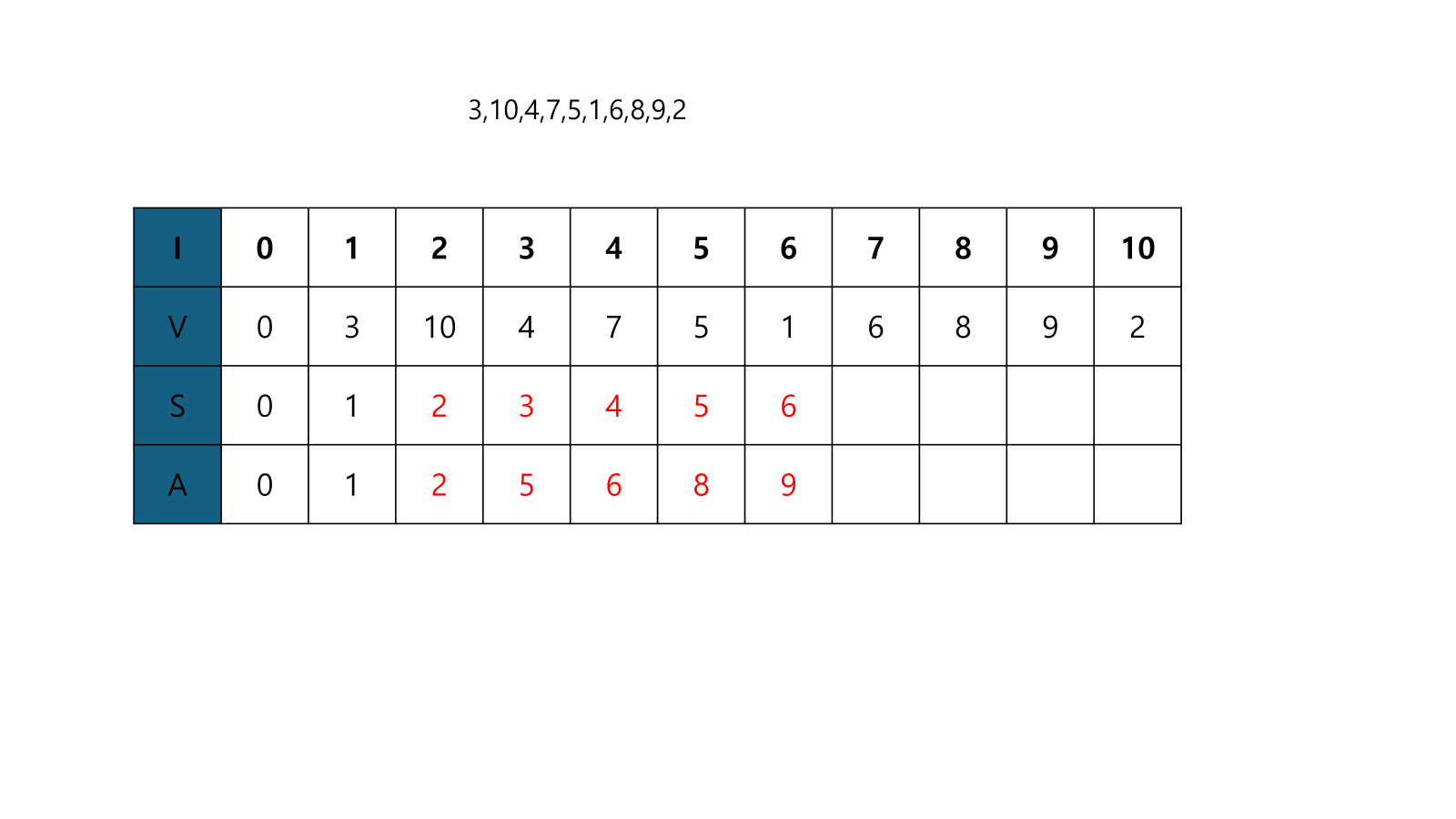
• 모두 진행된 모습이다.
• 여기서 S는 6번까지 채워졌으므로, LIS는 6의 길이를 가진다. 또한 9에서 끝나는 걸 알 수 있다. 그러므로 9에서 끝나면서, 점점 값이 올라가는 배열을 찾아보면 LIS를 알 수 있다.