최대 공백 정사각형

- n x n 크기의 흑백 이미지가 주어진다
- 검은 점들이 무작위로 찍혀있다.
- 가장 큰 정사각형을 구해라.
- 최소 비용 운동장 건설, 창고 세우기, 상점 열기, 우주선 / 드론의 이동방향등 여러가지 분야에 활용 될 수 있다.
- 가장 간단한 방법
- 정사각형의 크기 : n개
- 특정 크기에 대해서 안에 점이 존재하는지 검사 :
- 너무 오래 걸린다... 더 나은 방법은 없을까?
재귀적 서술
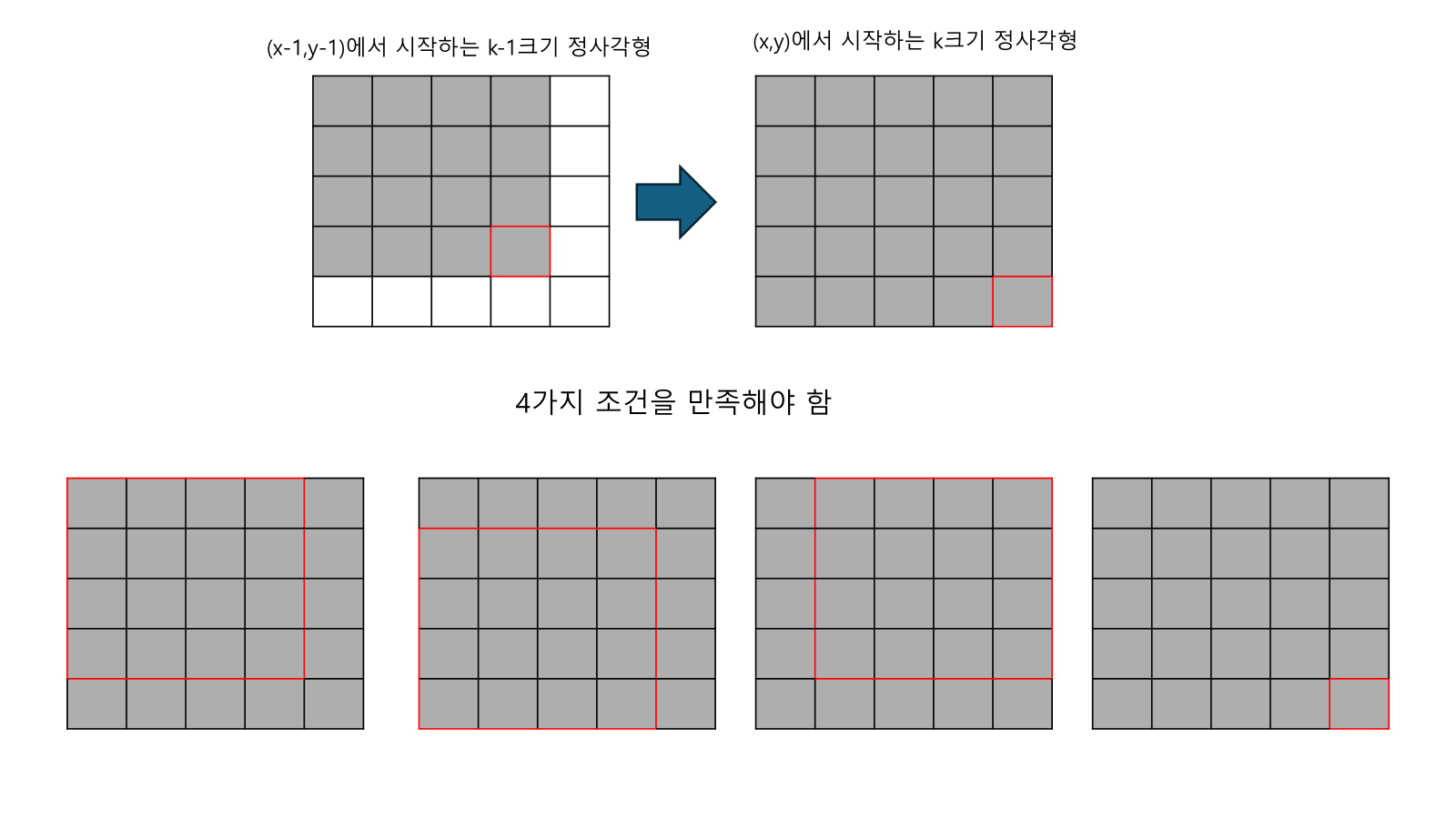
- m x m크기의 픽셀로 이루어진 정사각형 S가 비어있으면 다음 모두 성립
- S의 가장 우측 하단 픽셀이 비어있음
- 좌측 상단, 좌측 하단, 우측 상단의 크기 (m-1) x (m-1) 정사각형은 비어있음
- 역도 성립
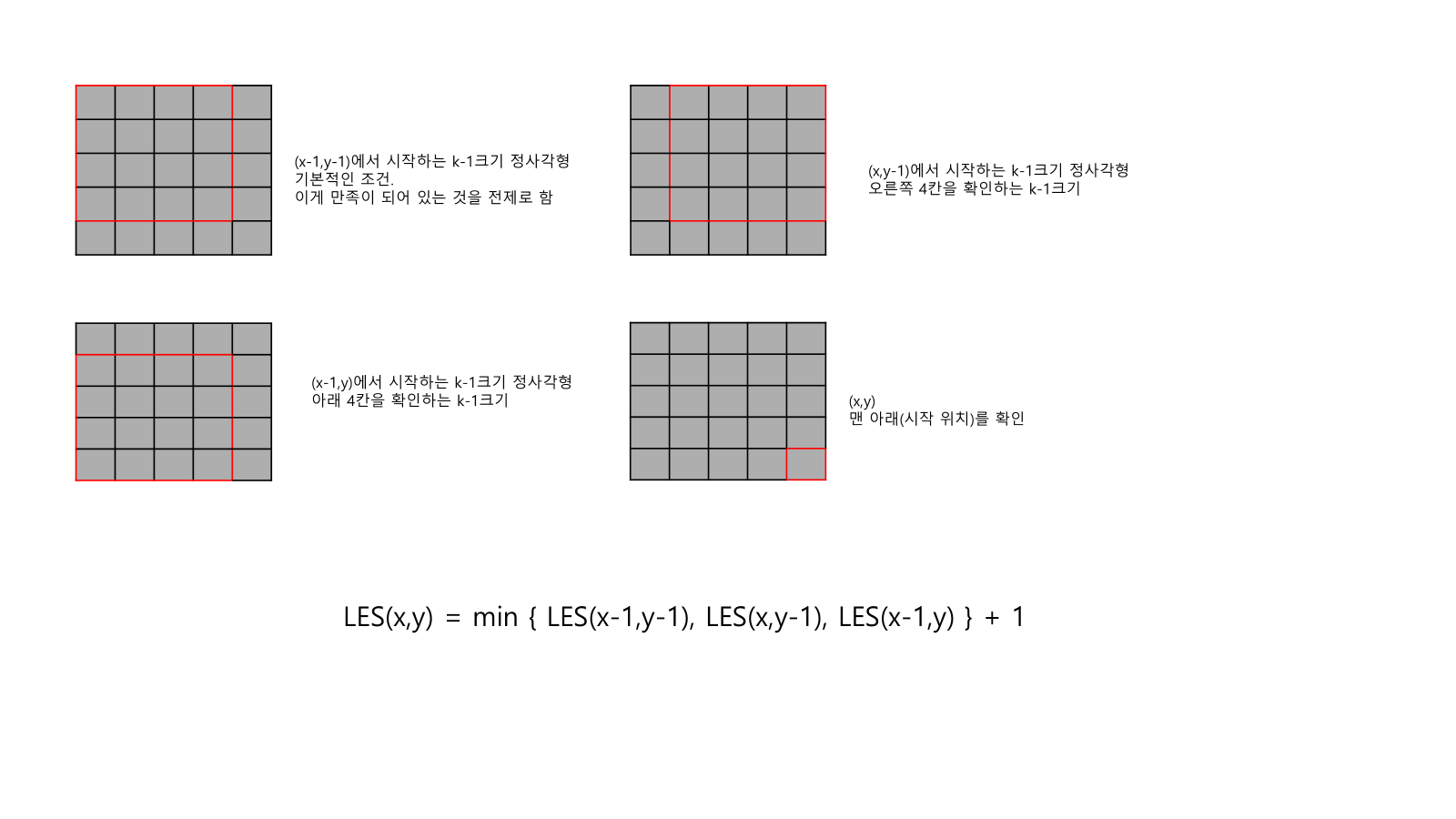
- LES(x,y) = 0
- 첫번째 행 또는 열의 픽셀이 비어있다면 LES(x,y) = 1
- 나머지 픽셀 (x,y)가 비어있다면 LES(x,y) = min{LES(x-1,y-1), LES(x-1,y), LES(x,y-1)}+1
Example
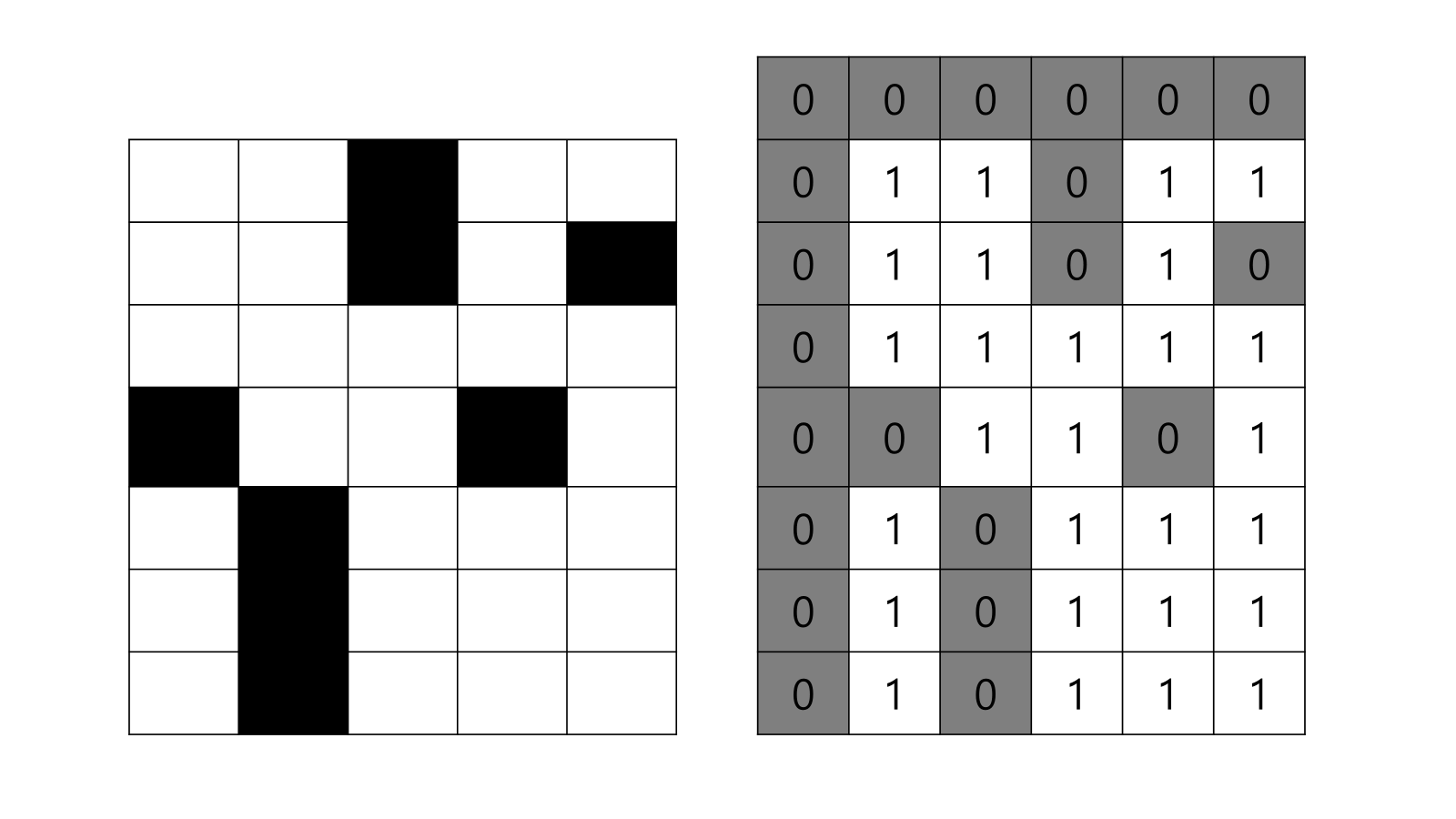
- 이 예시는 5*7 직사각형에서 수행한다. 크기는 직사각형이지만, 정사각형을 구하므로 알고리즘 자체는 달라지지 않는다.
- 먼저 직사각형 보다 한 칸 큰 6*8 배열을 만든다.
- 실제 직사각형을 , 배열을 라고 하자.
- 먼저 를 초기화 해주어야 한다.
- 의 (x,y) 좌표중 하나라도 0이면, 0으로 만든다.
- 의 (x,y) 값에 점이 찍혀있으면(0이면),
- 의 (x,y) 값이 비어있으면,
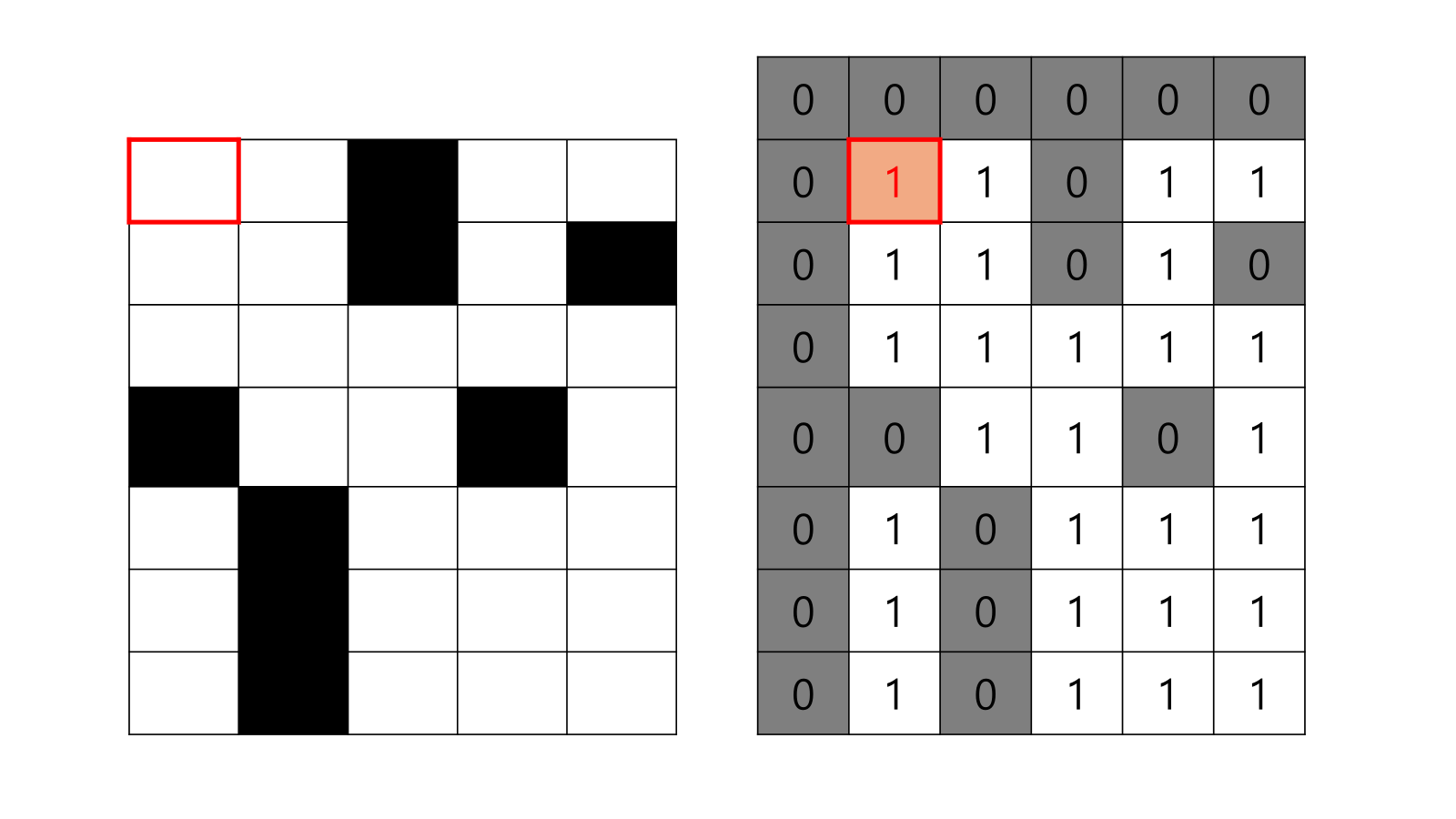
- 위부터 천천히 채워준다.
- S(x,y) = min{S(x-1,y-1), S(x-1,y), S(x,y-1)}+1
- 이에 따라서, S(1,1) = min{S(0,0), S(0,1), S(1,0)}+1 = min{0, 0, 0} + 1 = 0 + 1 = 1
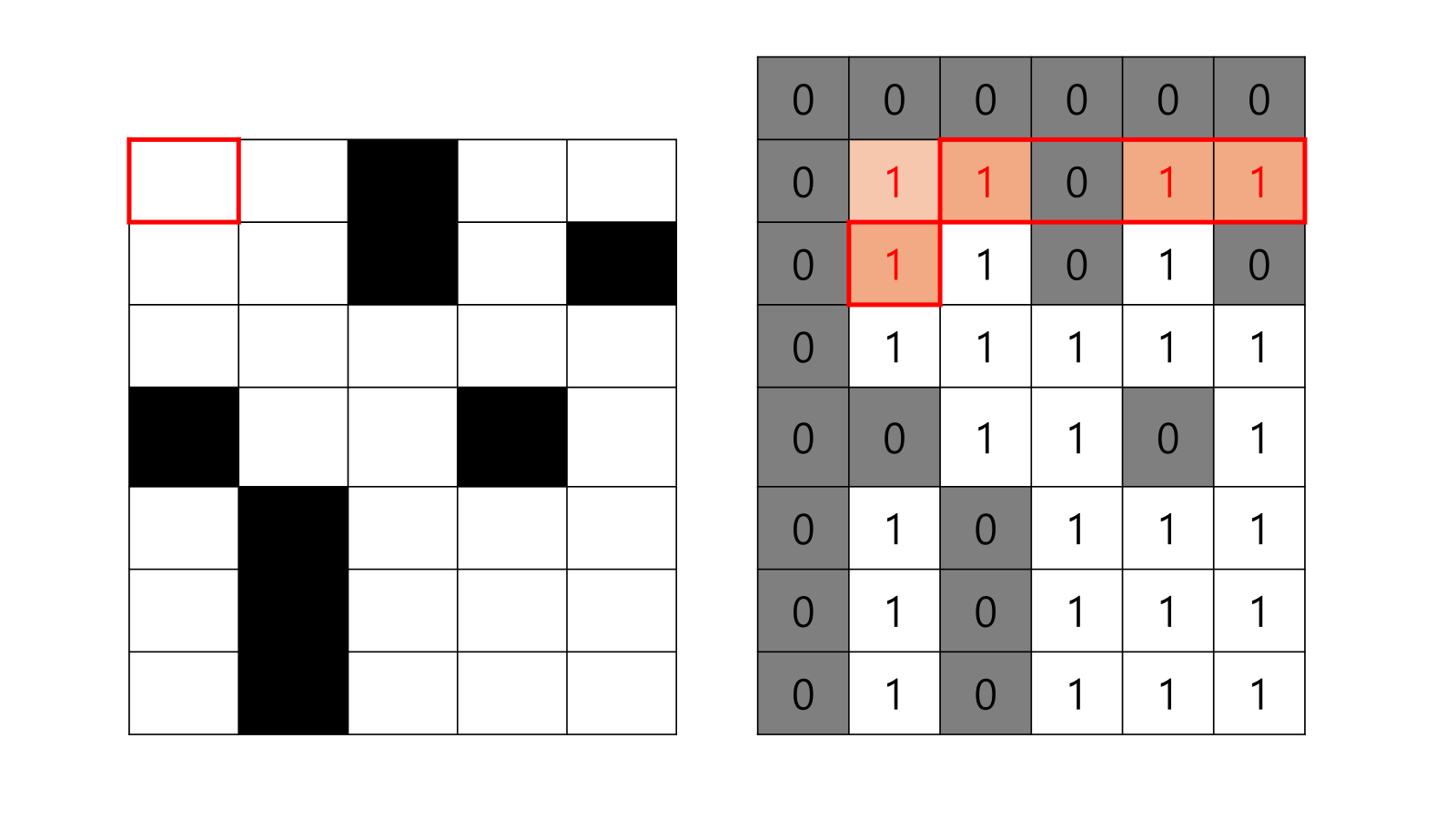
- 계속 진행한다. 이 때 진행을 위 왼쪽부터 아래 오른쪽으로 한다.
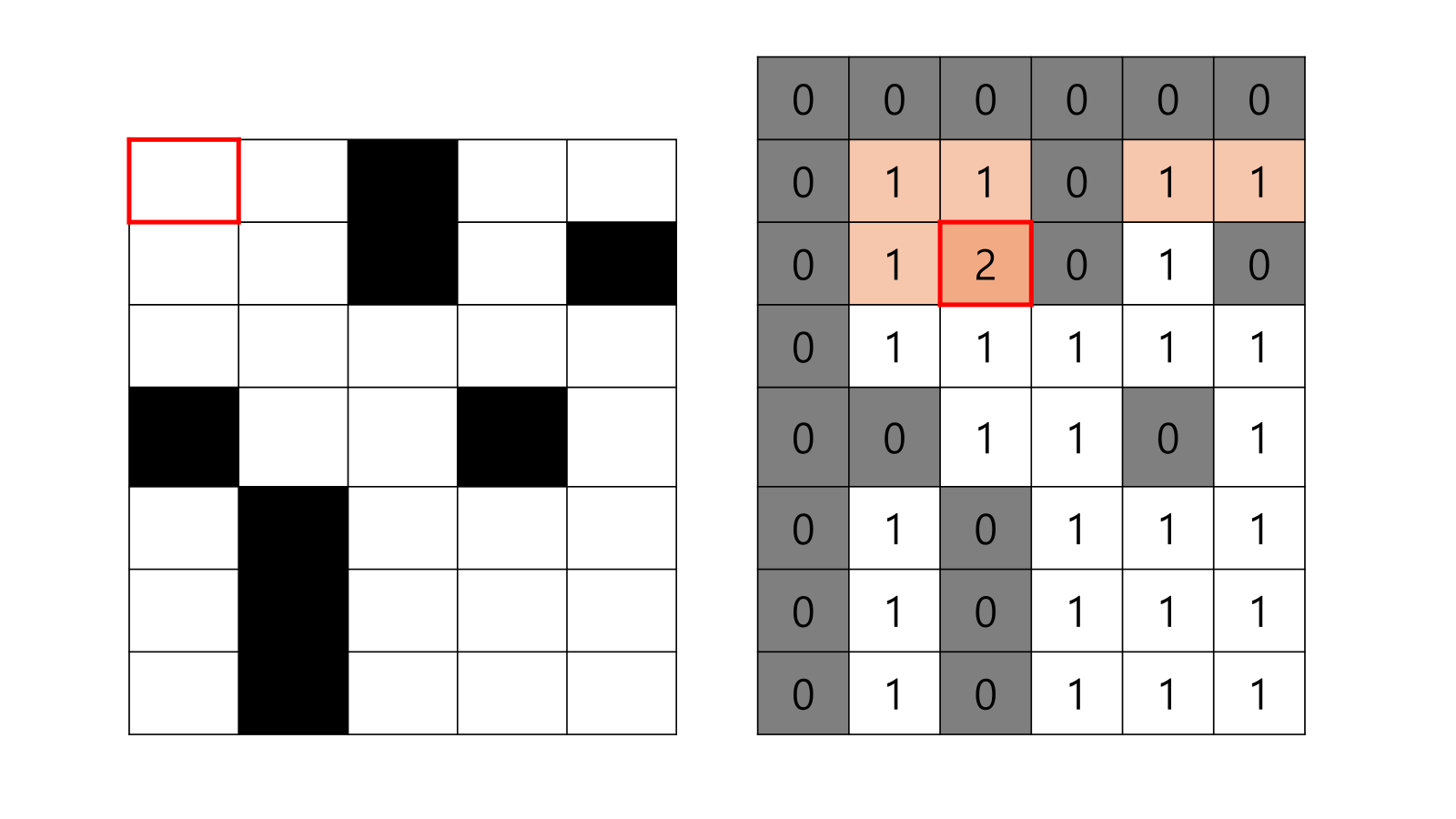
- S(x,y) = min{S(x-1,y-1), S(x-1,y), S(x,y-1)}+1
- 이에 따라서, S(2,2) = min{S(1,1), S(1,2), S(2,1)}+1 = min{1, 1, 1} + 1 = 1 + 1 = 2
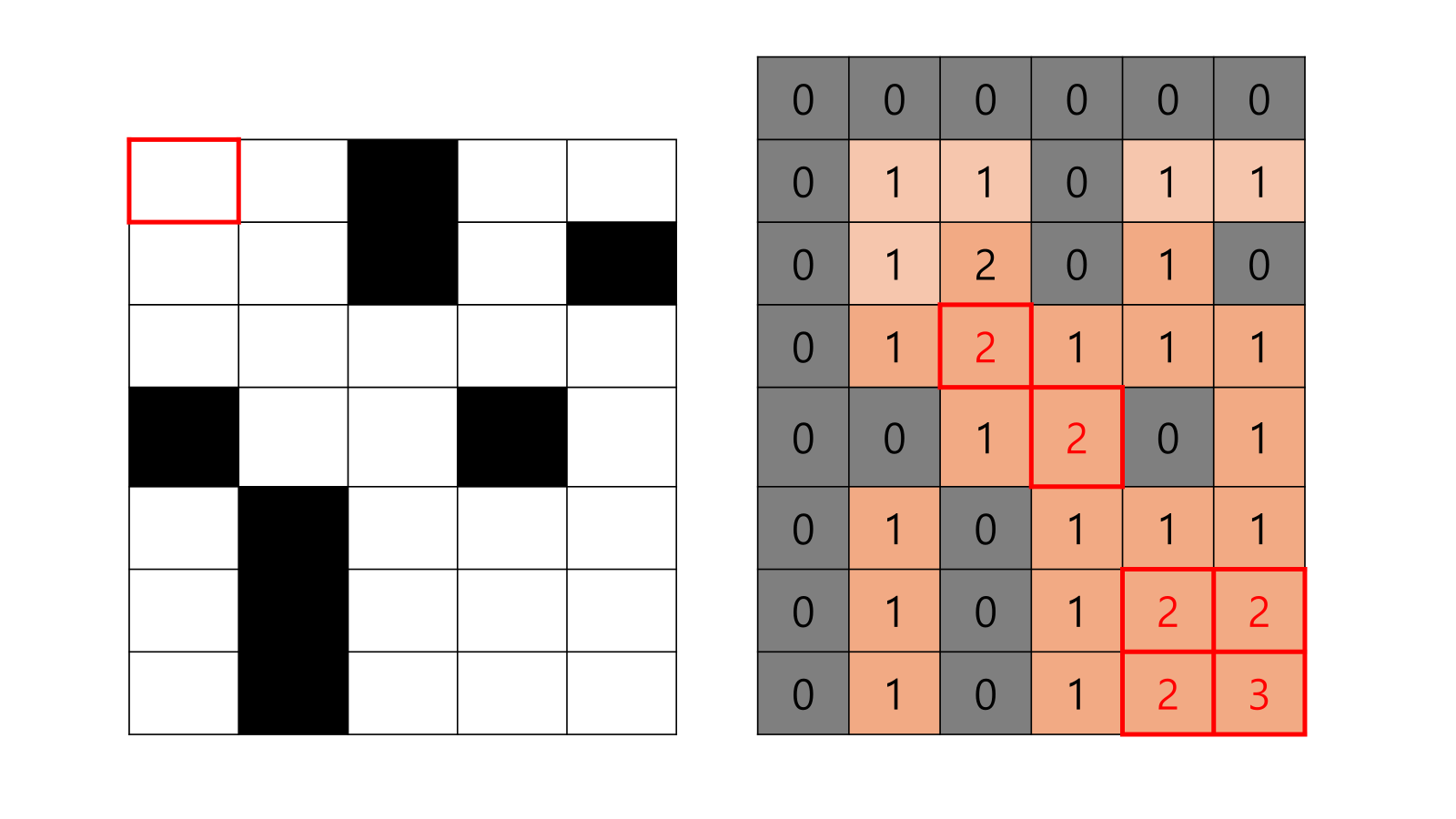
- 진행하면서, 원래 저장된 값보다 큰 값이 나오면 갱신한다.
- 끝까지 모두 바꿨으면, 결과값을 출력한다.
금화 모으기
- 시작점과 도착점이 있음
- 중간 중간에 금화들이 떨어져 있음
- 최단 거리로 나가면서 최대한의 금화를 모아야 함
- 모든 칸에 대해서 최대로 모은 금화를 구한다.
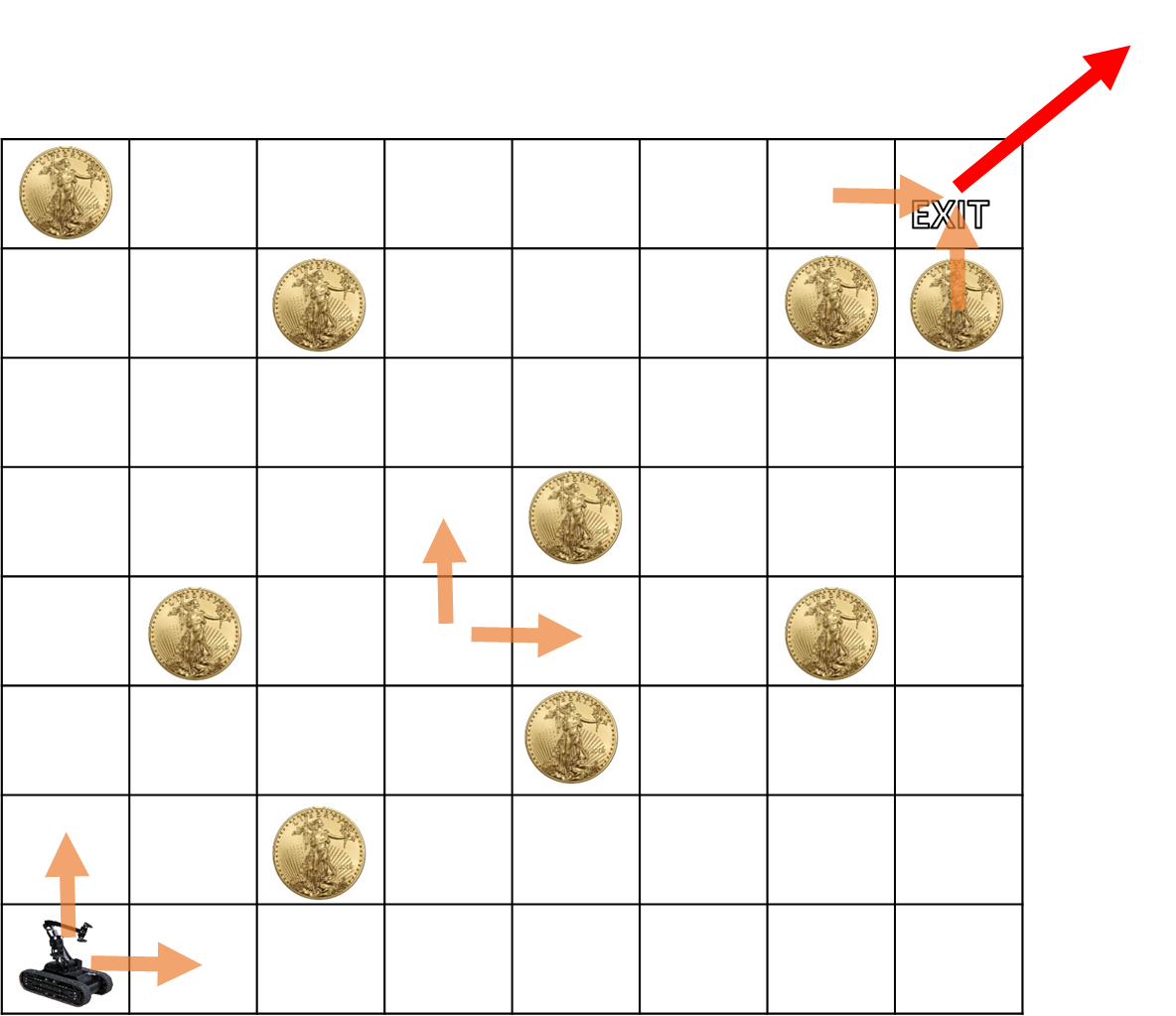
풀이법
: 칸에 도착할 때 까지 모을 수 있는 최대 금화 개수
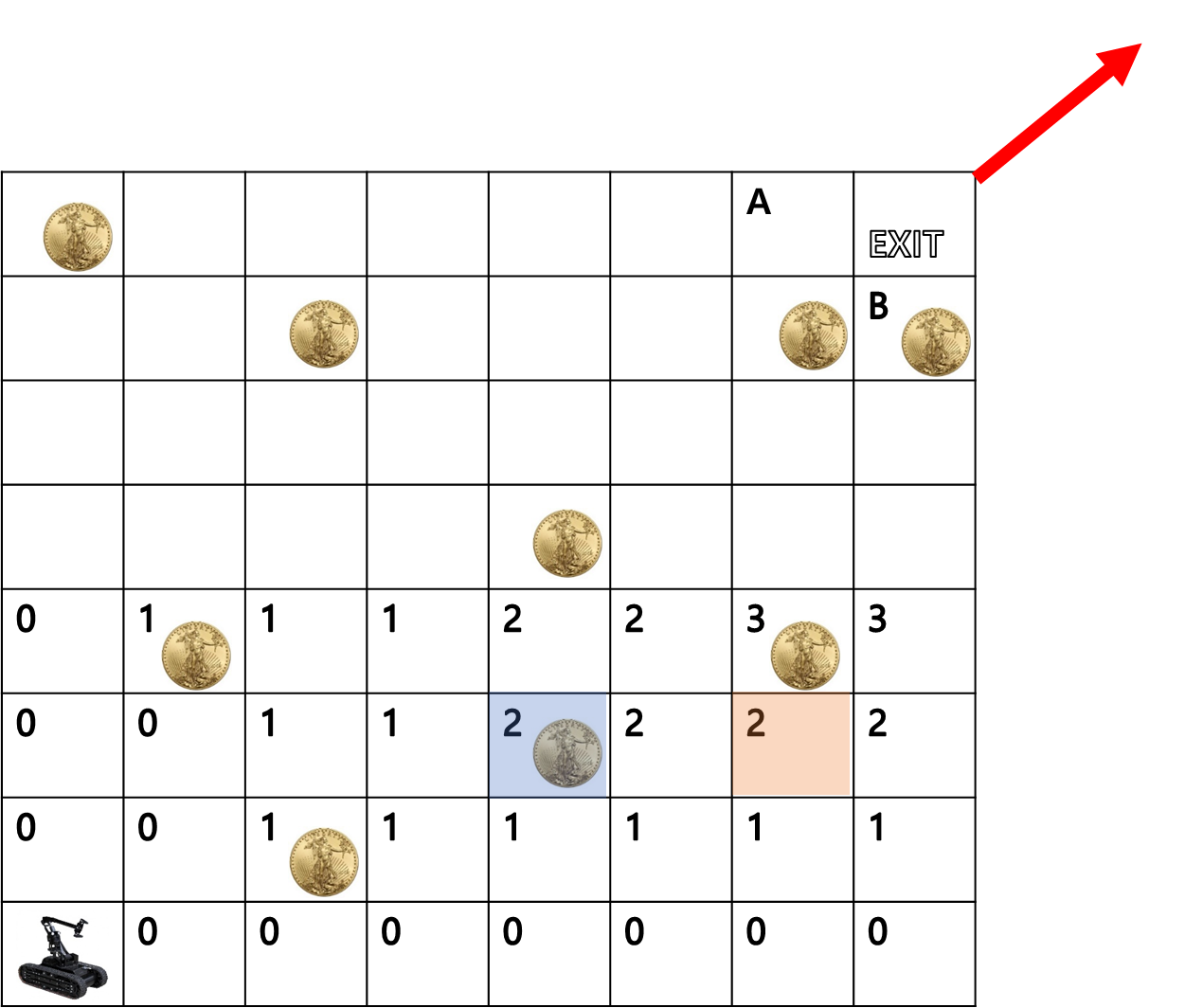
어려운 문제
- 정사각형 맵이 있음
- 왼쪽 아래서 오른쪽 위, 오른쪽 아래서 왼쪽 위로 총 2번 이동
- 한 칸에 금화가 여러개 있을 수 있음
풀이법
- 첫번째 시도를 , 두번째 시도를 라고 하자.
- 과 는 최소 1칸에서 최대 N칸 겹칠 수 있다.
- 여러번 겹치는 것 보단 한번만 겹치는 것이 무조건 좋다.
- 겹치는 칸은 두번째 시도에서 0이 되기 때문이다.
- 문제는 어느 칸이 겹치는가? 확인하기 위해 여러가지 방법을 시도할 수 있다.
- 일단, 모든 구석 자리는 답이 아니다.
- 모든 구석 자리는 2칸 이상 겹쳐야 함
- 이 말은 옆에 있는 1칸 자리가 겹치는 것이 나으므로 답이 아님
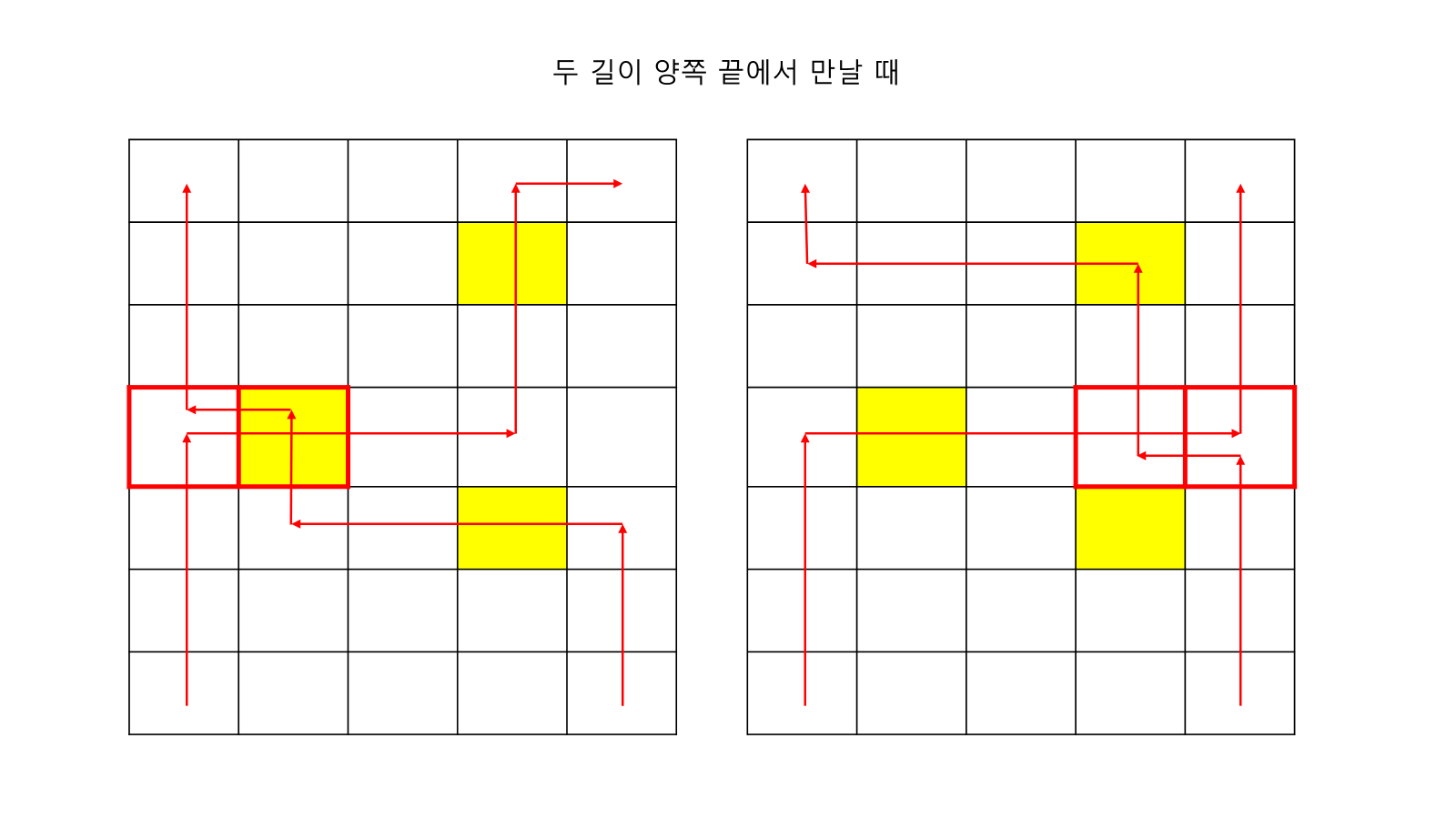
- 중간에서 만나기
- Case
- 먼저 왼쪽 아래 출발점에서 중간 지점으로 감
- 다음으로 오른쪽 위 도착점에서 중간 지점으로 감
- Case
- 먼저 오른쪽 아래 출발점에서 중간 지점으로 감
- 다음으로 왼쪽 위 도착점에서 중간 지점으로 감
- 가운데에서 만나는 것은 상,하,좌,우에서 오는 값을 더한 것
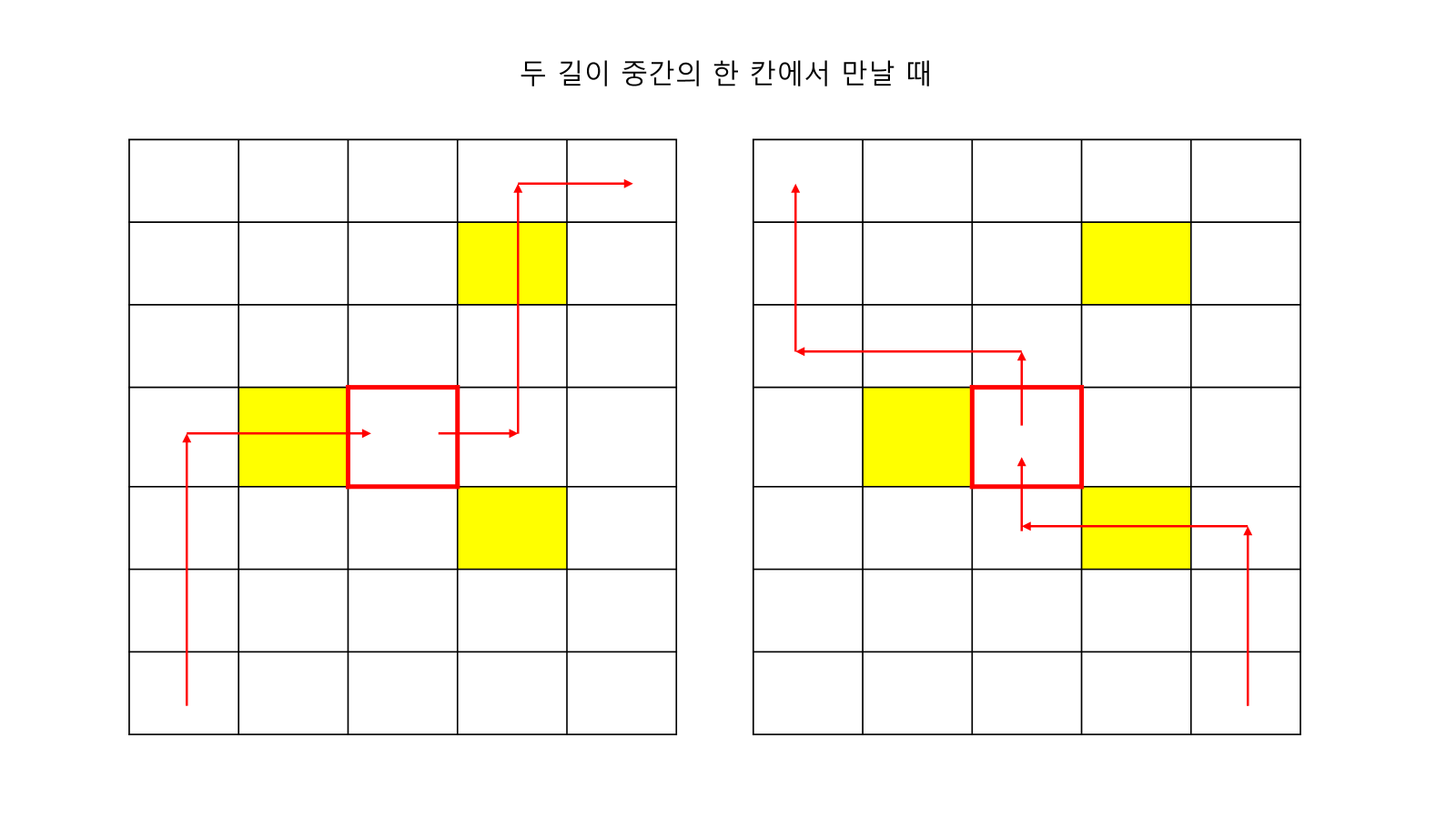
- 그러므로 왼쪽 아래 -> 오른쪽 위 / 윈쪽 위 -> 오른쪽 아래 / 오른쪽 아래 -> 왼쪽 위 / 오른쪽 위 -> 왼쪽 아래 4개를 DP함
- 이후 특정 칸에 대해서 상,하,좌,우,값을 구해서 답을 도출함
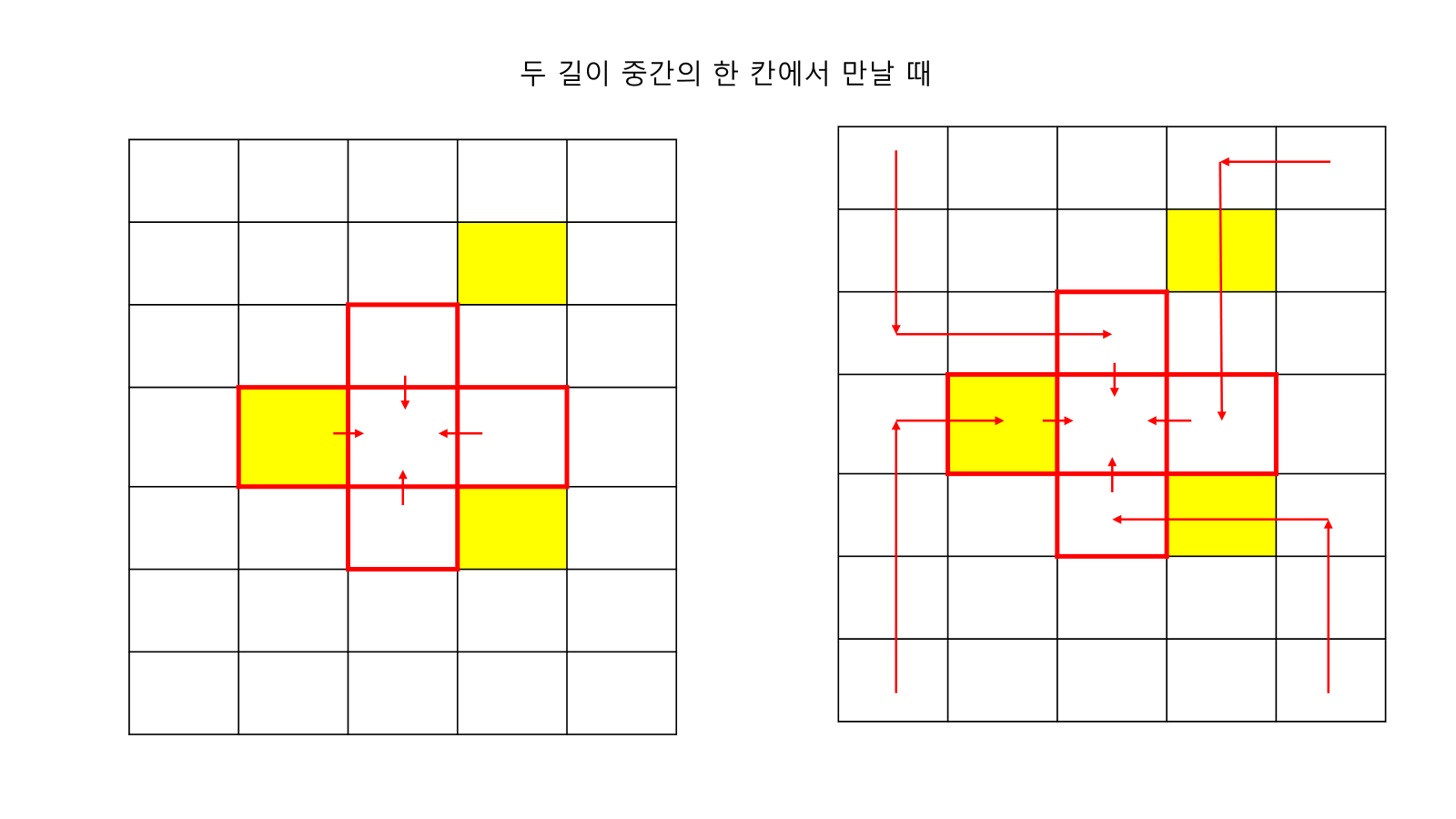
- Case
더 어려운 문제
- 칸에 음수가 존재
- 음수면 여러칸 겹치는 것이 답일 수 있음
- 그러면 직선 경로 모두에 대해서 해봐야함
- 이는 의 시간이 걸림
풀이법
- 한개의 줄을 선택한다.
- 맨 처음부터 시작했을 때 제일 좋은 Case를 먼저 구한다.
- 이후 맨 처음부터 하나씩 없애가며 제일 좋은 Case를 구한다.
- 맨 처음을 제거해도 제일 좋은 Case의 끝 값은 정해져 있다. 단지 위 아래로 값이 움직인다.
