[CA] CH3. Arithmetic for Computers

Chapter 3: Arithmetic for Computers

1. Operations on integers

Unsigned Integers: Binary to Octal and Hexadecimal

Signed Number

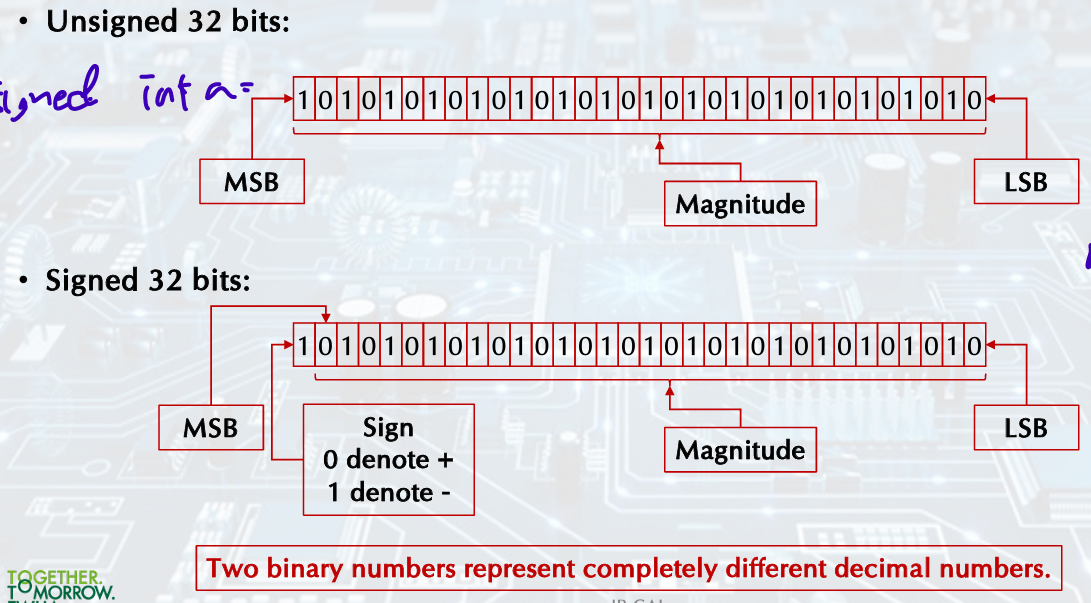
Integer Representation

(음수 나타내는 법)

1. Sign-and-magnitude representation: same magnitude, sign symbol distinguishes positive and negative
-> not well suited for use in computer +) need to compare and substract circuitry

2. 1's Complement Representation: K = (2$^n$ - 1) - P, oposite bit 0-1, 1-0 (K; negative number, P; positive number)
-> drawbacks in arithmetic operations

3. 2's Complement Representation: K = (2$^n$) - P, (10000000) - (00101010)

1's & 2's Complement Representation
K1 = (2$^n$ - 1) - P
k2 = (2$^n$) - P
K2 = K1 + 1
K2<->P: flip 하다가 마지막 1부터는 그대로 마지막 1기준 왼쪽은 flip, 오른쪽은 그대로

Addition, Substraction

1's Complement

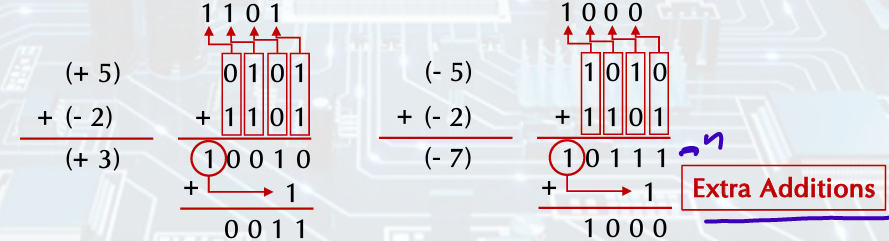
2's Complement

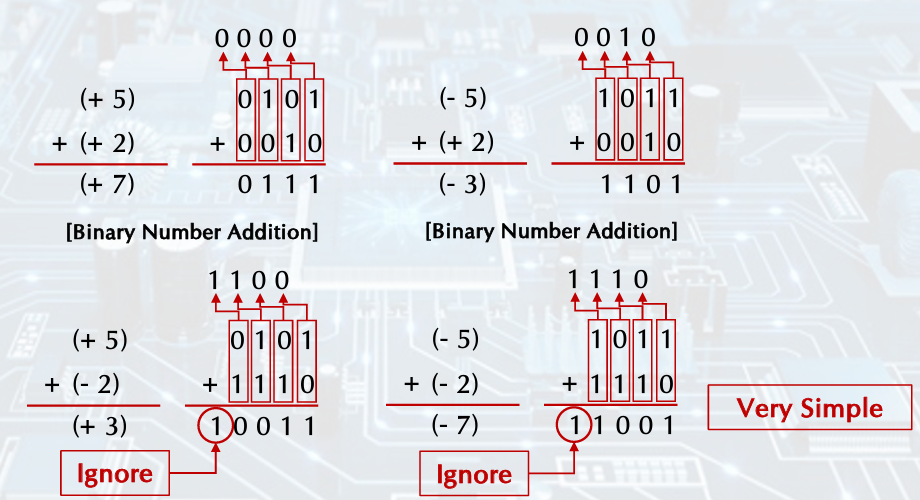
substraction: (+5) - (+2) -> (+5) + (-2) = (+3) 부호 바꿈

2. Overflow

Overflow Conditions for Addition and Substraction

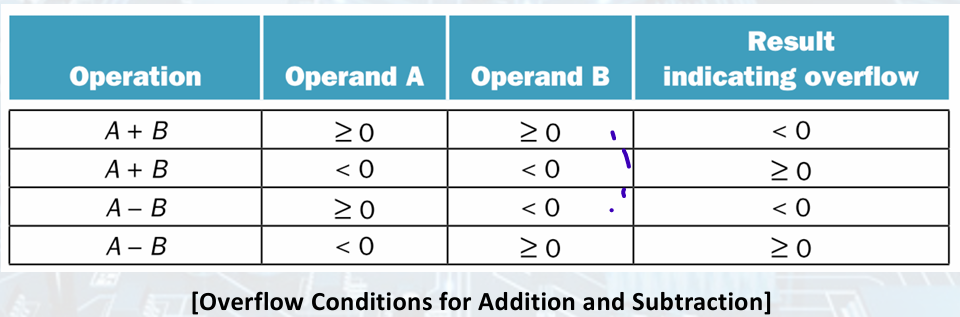
Overflow if result out of range.
• Adding +value and -value operands, no overflow.
• Adding two +value operands, Overflow if result sign is 1.
• Adding two value operands, Overflow if result sign is 0.

Overflow if result out of range.
• Subtracting two +value or two value operands, no overflow.
• Subtracting +value from value operand, Overflow if result sign is 0.
• Subtracting value from +value operand, Overflow if result sign is 1.

Arithmetic Logic Unit (ALU)

: the device that performs the arithmetic operations like addition and subtraction or logical operations like AND or OR.

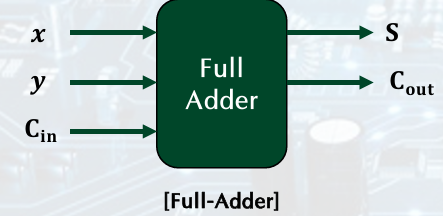
1. Full Adder
1-Bit

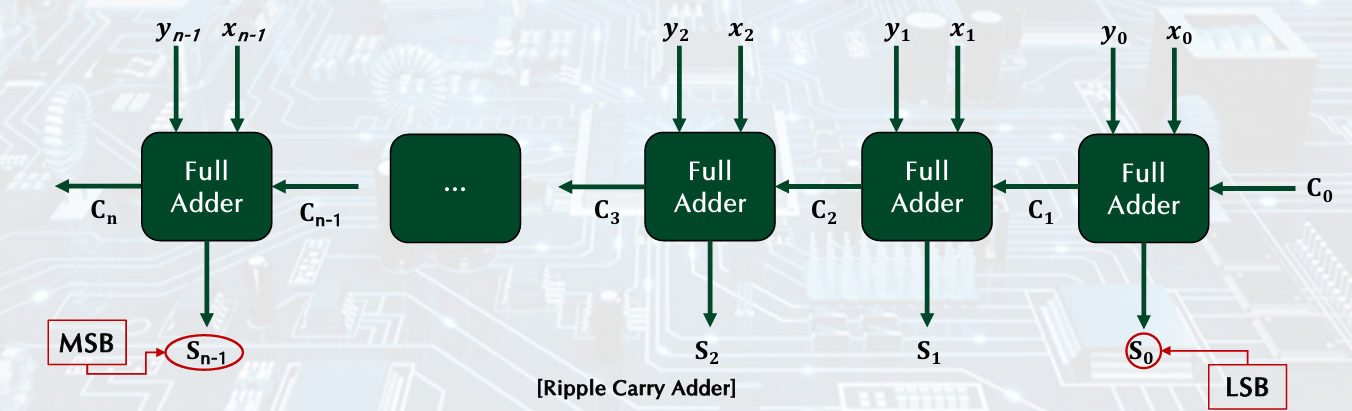
2. Ripple Carry Adder
Simply connecting full adders. Previously calculated carry value is propagated to the next full adder.

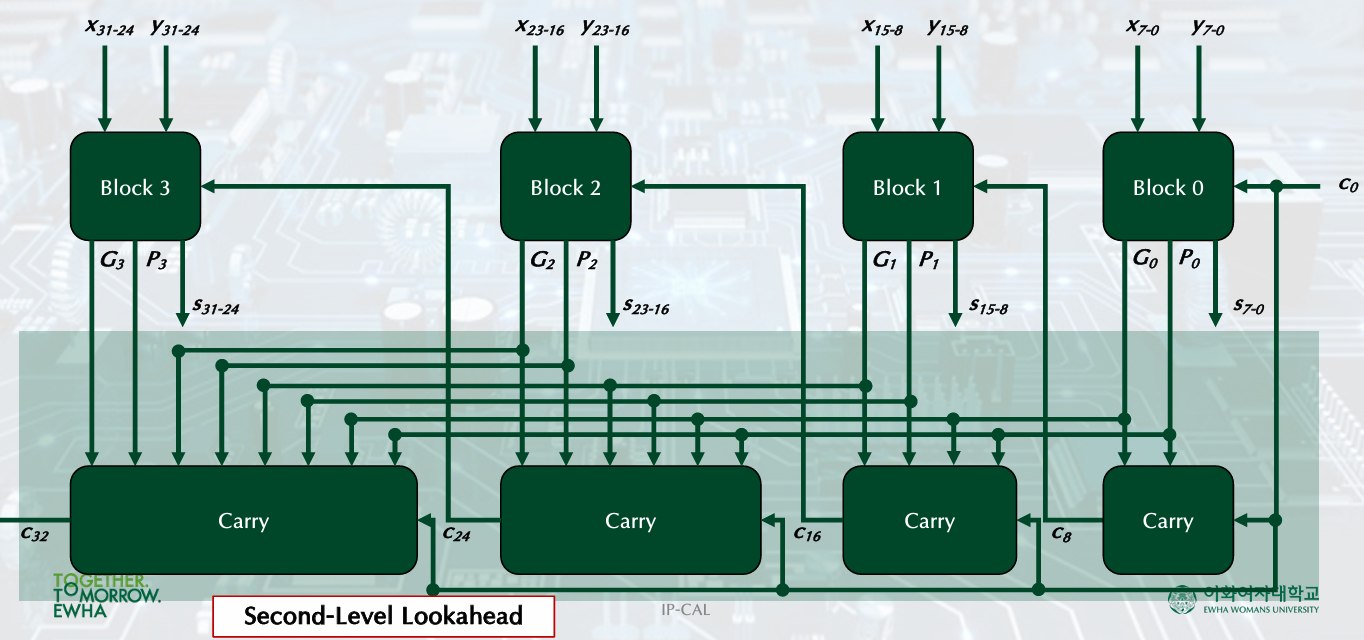
3. A Hierarchical Carry-Lookahead Adder

Substractor
: necessary to use 2's complement of one operand, others are same as adder

Arithmetic for Multimedia
•Graphics and media processing operate on vectors of 8-bit and 16-bit data.
Use a 64-bit adder, with a partitioned carry chain.
Operate on 8×8-bit, 4×16-bit, or 2×32-bit vectors.
SIMD (single-instruction, multiple-data).
• Saturating operations:
On overflow, the result is the largest representable value.
c.f. 2s-complement modulo arithmetic.
E.g., clipping in audio, saturation in video.

Multiplication

(Unsigned Number)

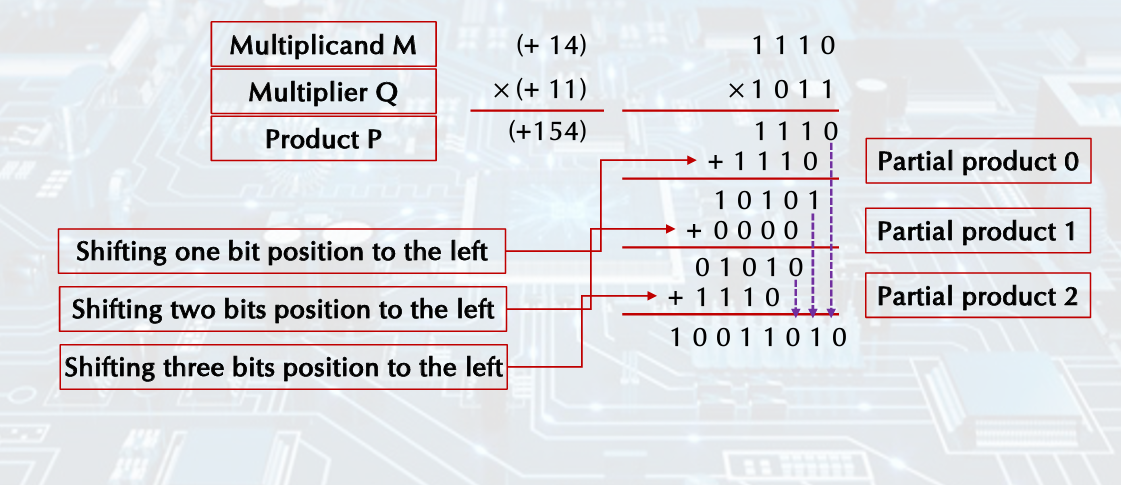
Multiplication Hardware

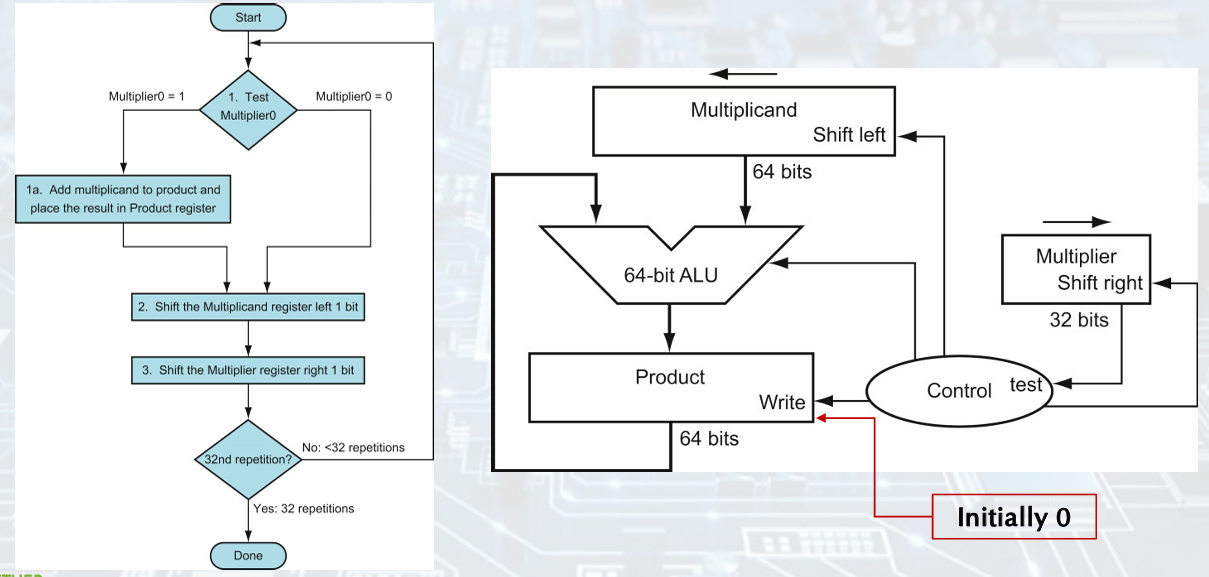
Optimized Multiplier

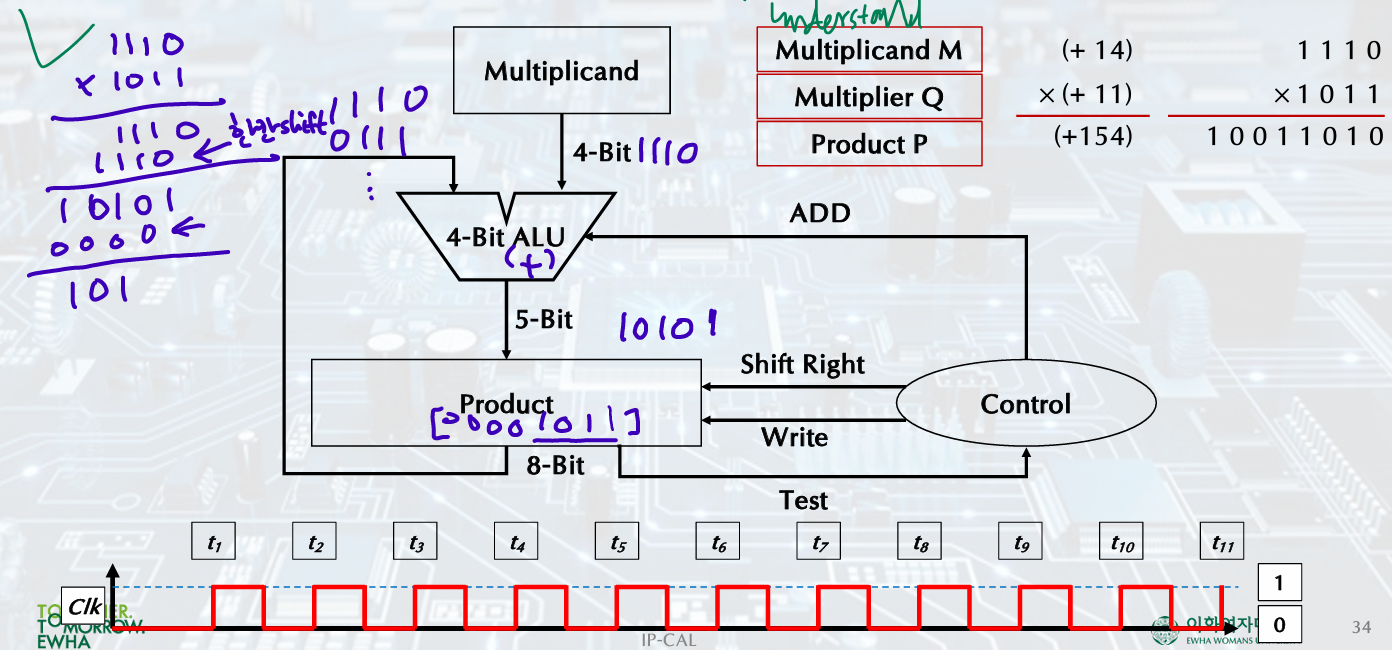
Product
0000 1011 (Multiplier Q) + 1110 0000 (마지막이 1)
0111 0101 + 1110 0000 (마지막이 1) (더하고 right shift)
1010 1010 + 0000 0000 (마지막이 0)
0101 0101 + 1110 0000 (마지막이 1)
1001 1010

Faster Multiplier: uses multiple adders, cost/performance tradeoff

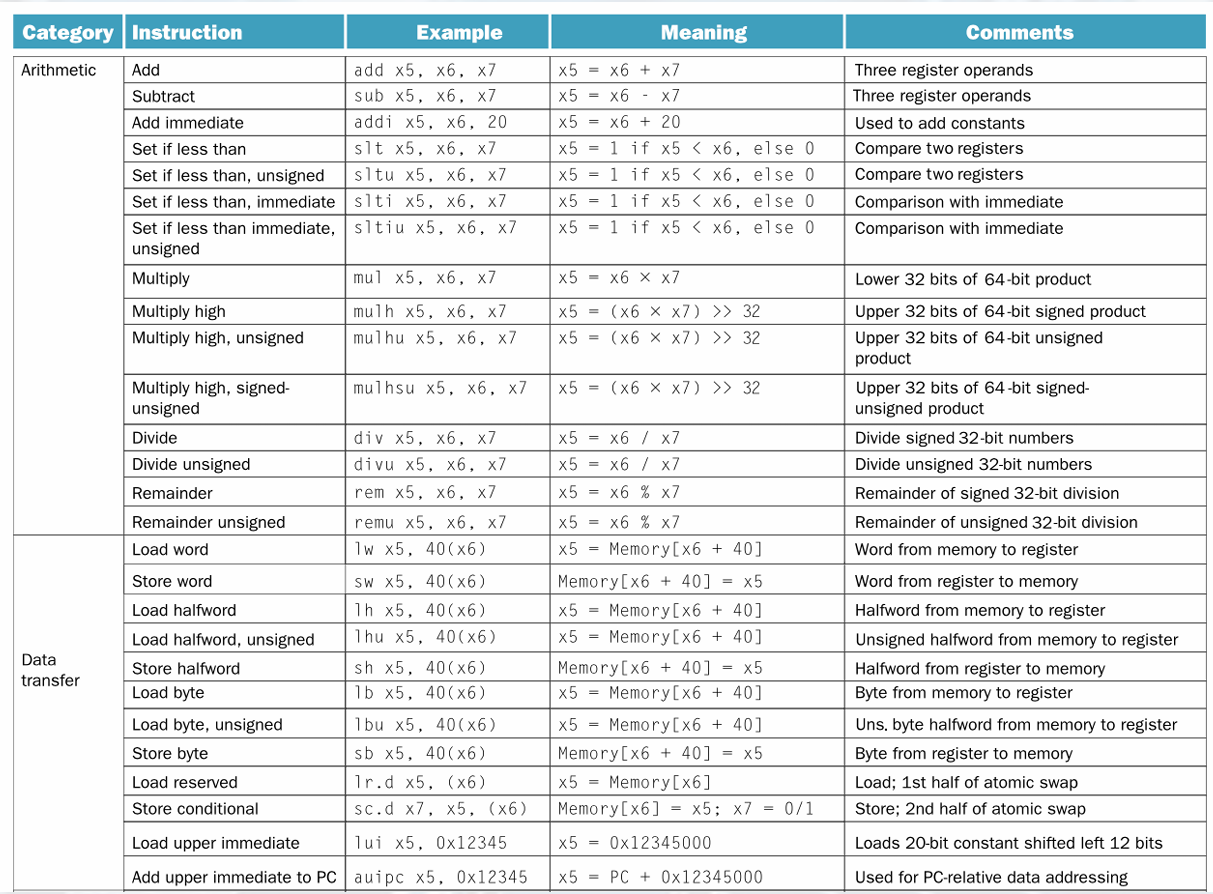
RISC-V Multiplication (instructions)
mul: multiply, lower 32 bis of product
mmulh: multiply high, upper 32 bits of the product, signed operands
mulhu: unsigned
mulhsu: one signed/ one unsigned

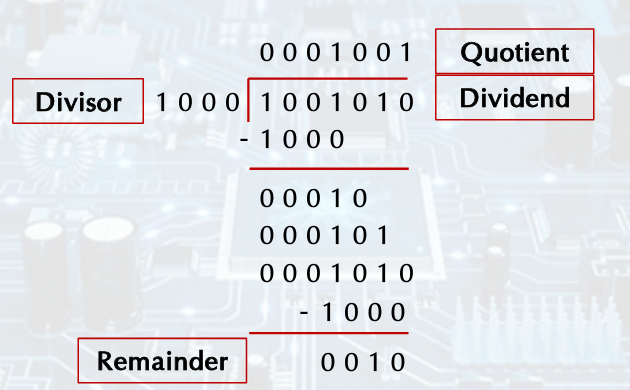
Division

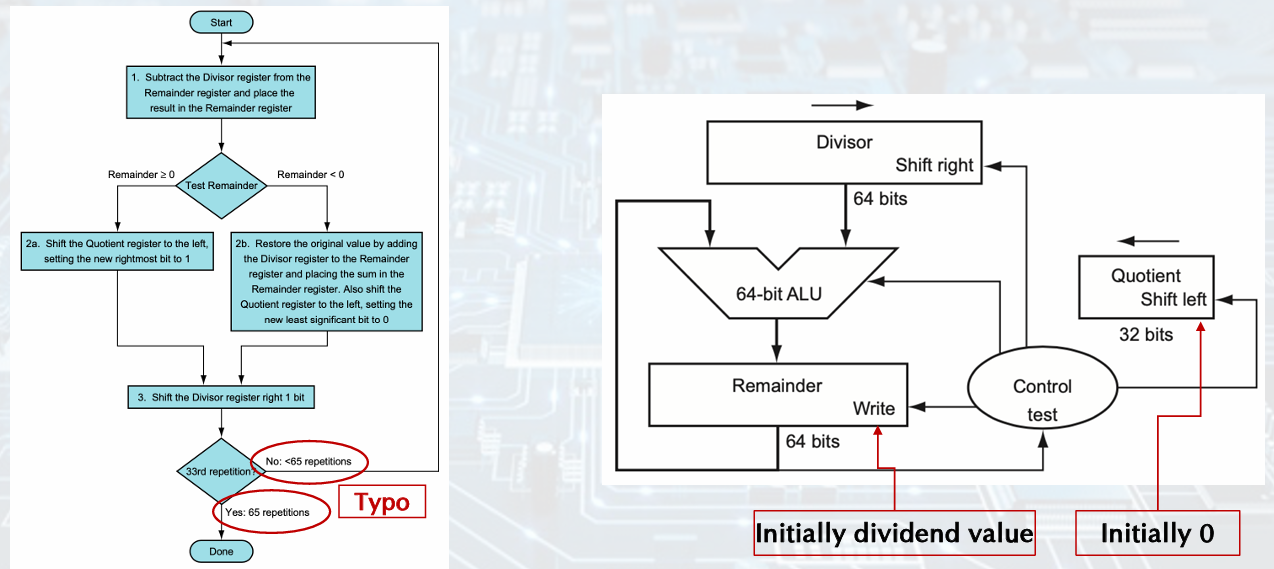
Division Hardwrare

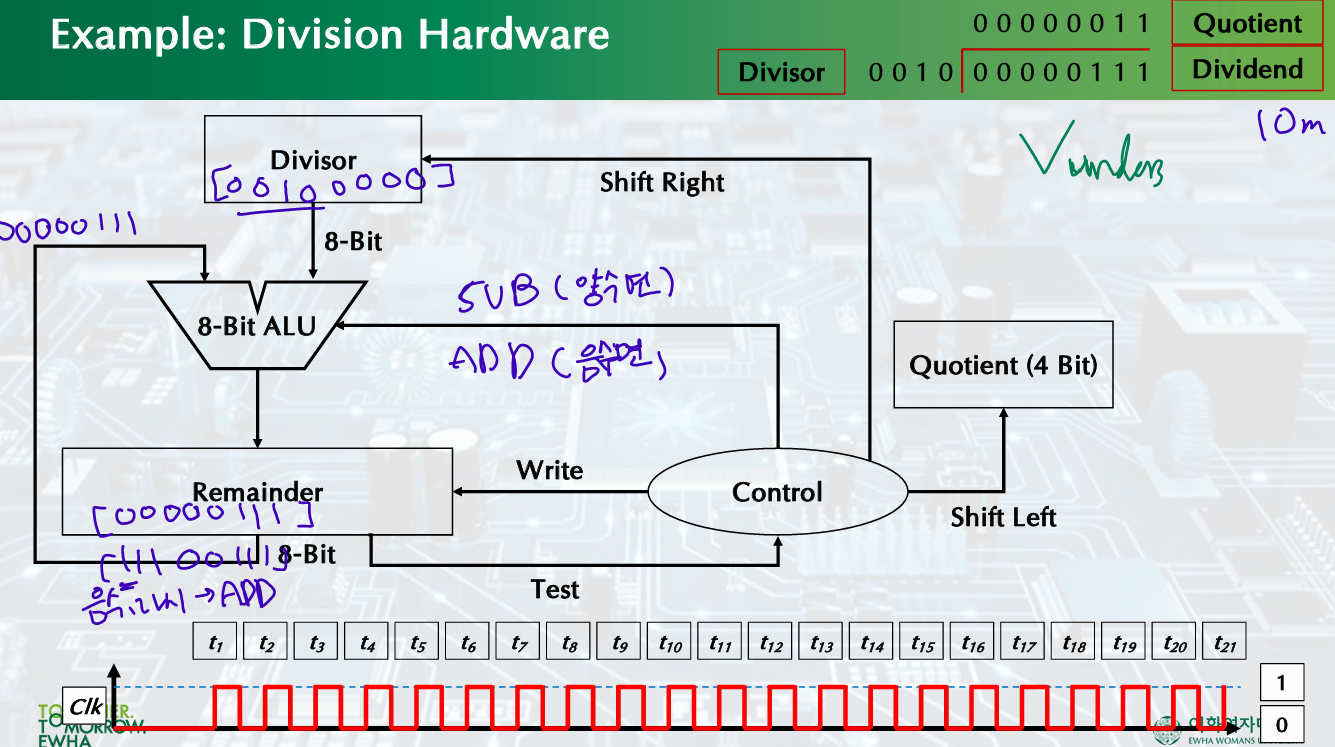
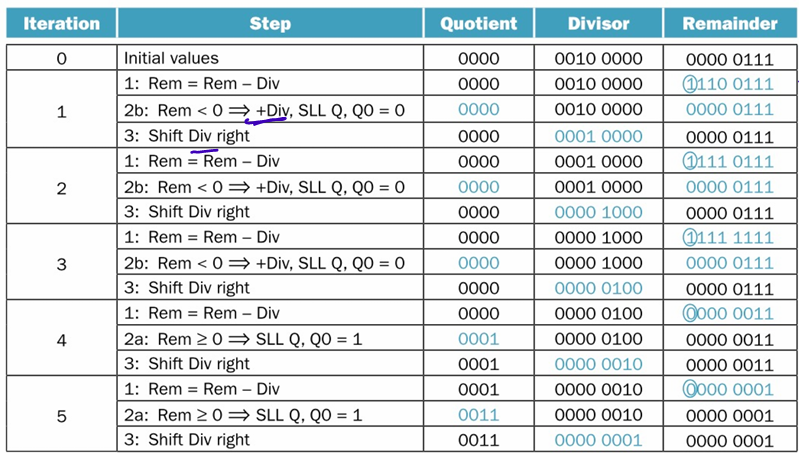
Divisor 0010 0000, Reminder 0000 0111, Quotient 0000
shift right, rem - div < 0, qu = 0 and shift left
shift right, rem - div >= 0 rem -= div, qu = 1 and shift left

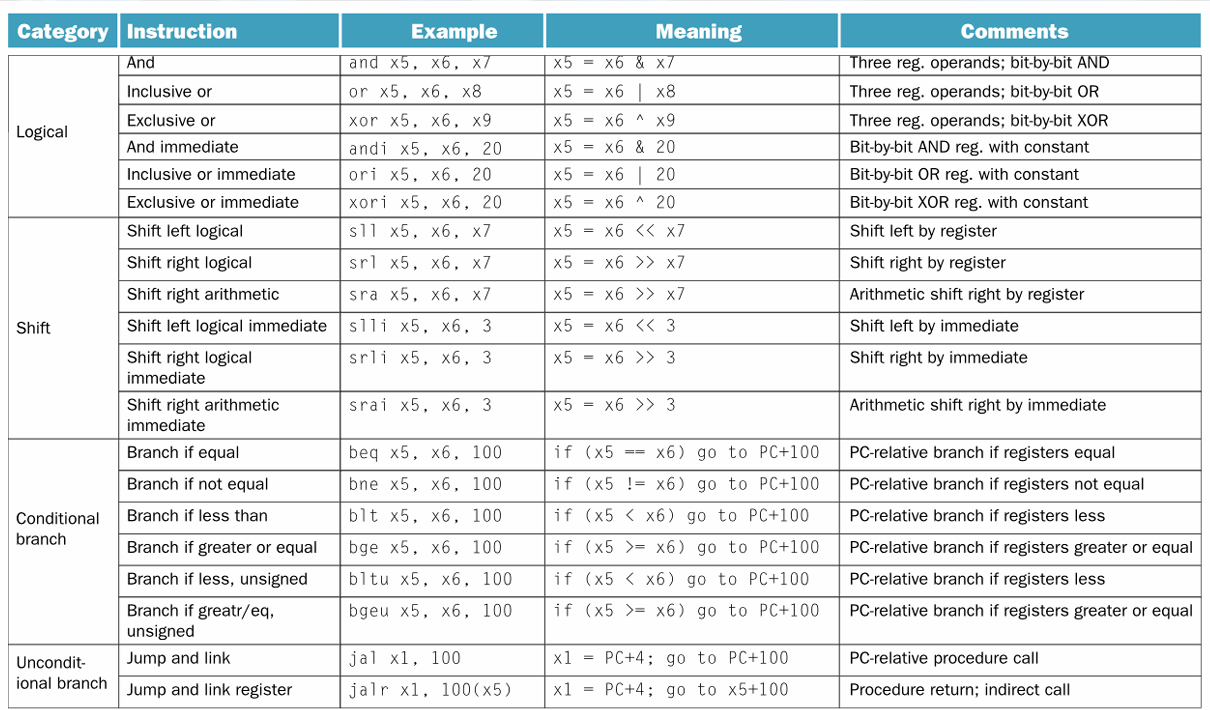
RISC-V Division (Instruction)
• div: signed divide.
• rem: signed remainder.
• divu: unsigned divide.
• remu: unsigned remainder.
• Overflow and division-by-zero don’t produce errors.
Just return defined results.
Faster for the common case of no error.

3. Floating Point

• Normalized form: $\pm 1.xxxxxxx \times 2^{yyyy}$
• Two representations:

Single precision (32-bit):
smallest: $\pm 1.0\times 2^{-126} ~ \pm 1.2\times 10^{-38}$
largest:$\pm 2.0\times 2^{127} ~ \pm 3.4\times 10^{38}$

Double precision (64-bit):
smallest: $\pm 1.0\times 2^{-1022} ~ \pm 2.2\times 10^{-308}$
largest: $\pm 2.0\times 2^{1023} ~ \pm 1.8\times 10^{308}$

IEEE Floating-Point Format

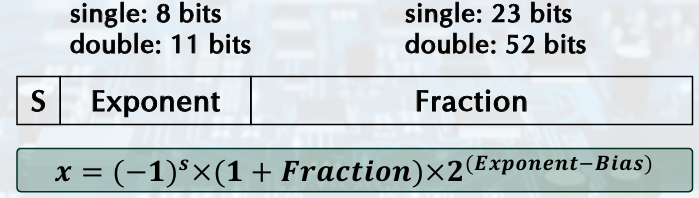
S: sign bit
Normalize significand: Fraction with '1' restored(hidden bit, F + 1), 1.0 <= |significand| < 2.0
0.ffff = f$\times 2^{-1}$ + f$\times 2^{-2}$..
Exponent: actual + bias: excess representation
unsigned, Single bias = 127, Double bias = 1023

Example.
-0.75 -> single: 1011 1111 0100 0...00, double: 1011 1111 1110 1000 0...00.
single 1100 0000 1010 00...00 -> -5.0

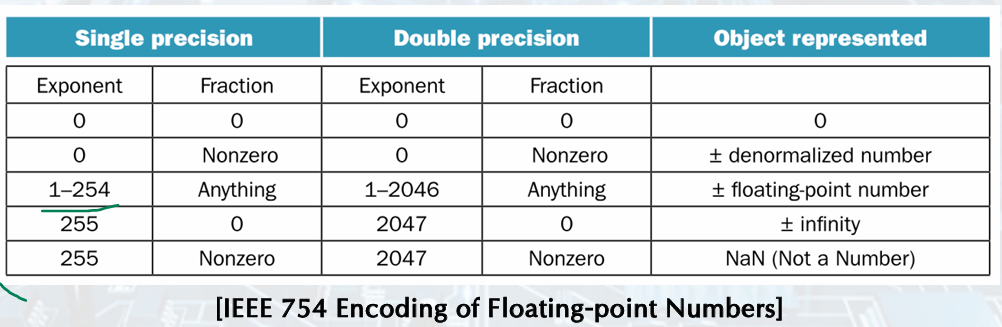
Floatinng-Point Addition

$(1.000_2 \times 2^{-1}) + (-1.110_2\times 2^{-2}) = (0.5 + (-0.4375))$
1. Align binary points.
• Shift number with smaller exponent.
$(1.000_2 \times 2^{-1}) + (-0.111_2\times 2^{-1})$
2. Add significands.
$(1.000_2 \times 2^{-1}) + (-0.111_2\times 2^{-1}) = (0.001_2\times 2^{-1})$
3. Normalize result & check for over/underflow.
$(1.000_2\times 2^{-4})$ with no over/underflow
4. Round and renormalize if necessary.
(1.000_2\times 2^{-4}) = 0.0625

FP Adder Hardware
• Much more complex than integer adder.
• Doing it in one clock cycle would take too long.
Much longer than integer operations.
Slower clock would penalize all instructions.
• FP adder usually takes several cycles.
Can be pipelined.

Floating-Point Multiplication

$(1.000_2\times 2^{-1})\times(-1.110_2 \times 2^{-2}) = 0.5\times -0.4375$
1. Add exponents.
• Unbiased: (-1) + (-2) = -3
• Biased: (-1 + 127) + (-2 + 127) = -3 + 254 - 127 = -3 + 127
2. Multiply significands.
$1.000_2\times 1.110_2 = 1.110_2$->$1.110_2\times 2^{-3}$
3. Normalize result & check for over/underflow.
$1.110_2\times 2^{-3}$ (no change) with no over/underflow.
4. Round and renormalize if necessary.
$1.110_2\times 2^{-3}$ (no change).
5. Determine sign: +ve × -ve -> ve.
$-1.110_2\times 2^{-3} = −0.21875$

FP Arithmetic Hardware
• FP multiplier is of similar complexity to FP adder.
But uses a multiplier for significands instead of an adder.
• FP arithmetic hardware usually does.
Addition, subtraction, multiplication, division, reciprocal, square-root.
FP ßàinteger conversion.
• Operations usually takes several cycles.
Can be pipelined.

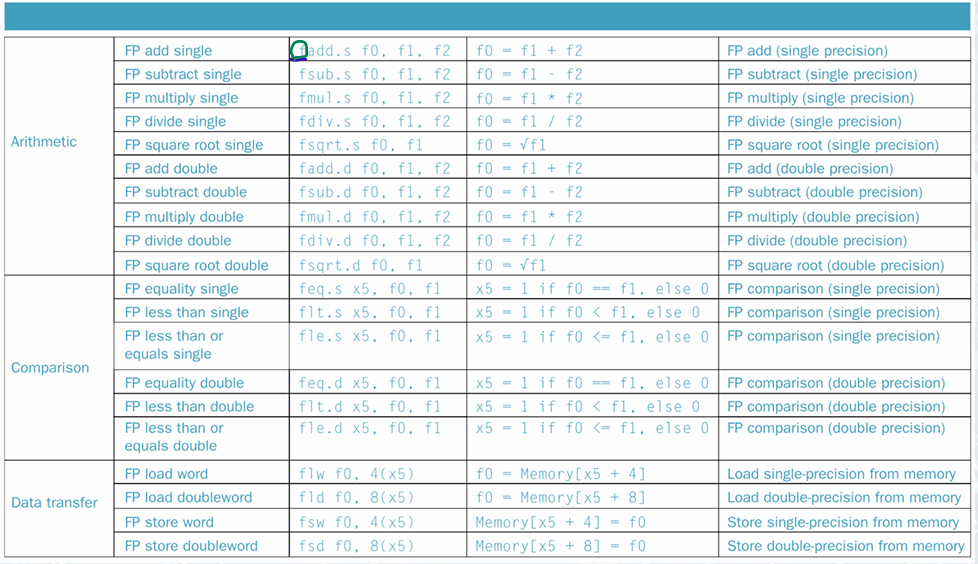
FP Instructions in RISC-V
32 floating-point registers: f0-f31: An f-registers can hold either a single-precision floating-point number or a double-

Associativity

Concluding remarks

• Bits have no inherent meaning.
Interpretation depends on the instructions applied.
• Computer representations of numbers.
Finite range and precision.
Need to account for this in programs.
• ISAs support arithmetic.
Signed and unsigned integers.
Floating-point approximation to reals.
• Bounded range and precision.
Operations can overflow and underflow.