[GN] 1,2. Fundamentals on Graph, Random Graph Generation

HW1을 위한 전체 정리

Week 1-2. Fundamentals on Graph

1. Network & Applications

Graph Example: Social Networks, Social Circle Detection, Content Propagation, Blogger Connections, Information Cascades 폭포, Multi-layered Graph
Application: Recommendation, Interest Graph, Polarization, Virality
Do: Node classification, Link prediction, Community detection, Network similarity, graph-based algorithms

2. Graph Basic & Modeling

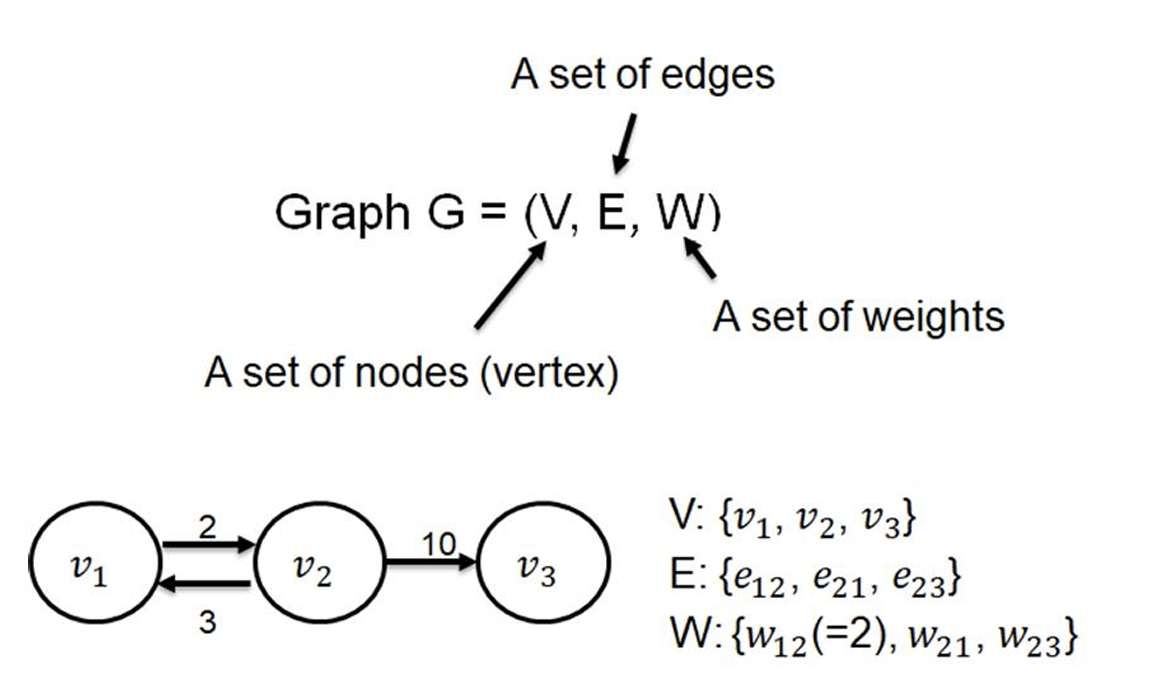
Components of a network
• Objects: nodes, vertices
• Interactions: links, edges
• System: network, graph

Graph Types
Undirected Graph: a - b
Directed Graph: a -> b
Unweighted Graph: a 1-> b

• Complete Graph: undirected graph with the number of edges E = Emax(N(N-1)/2)
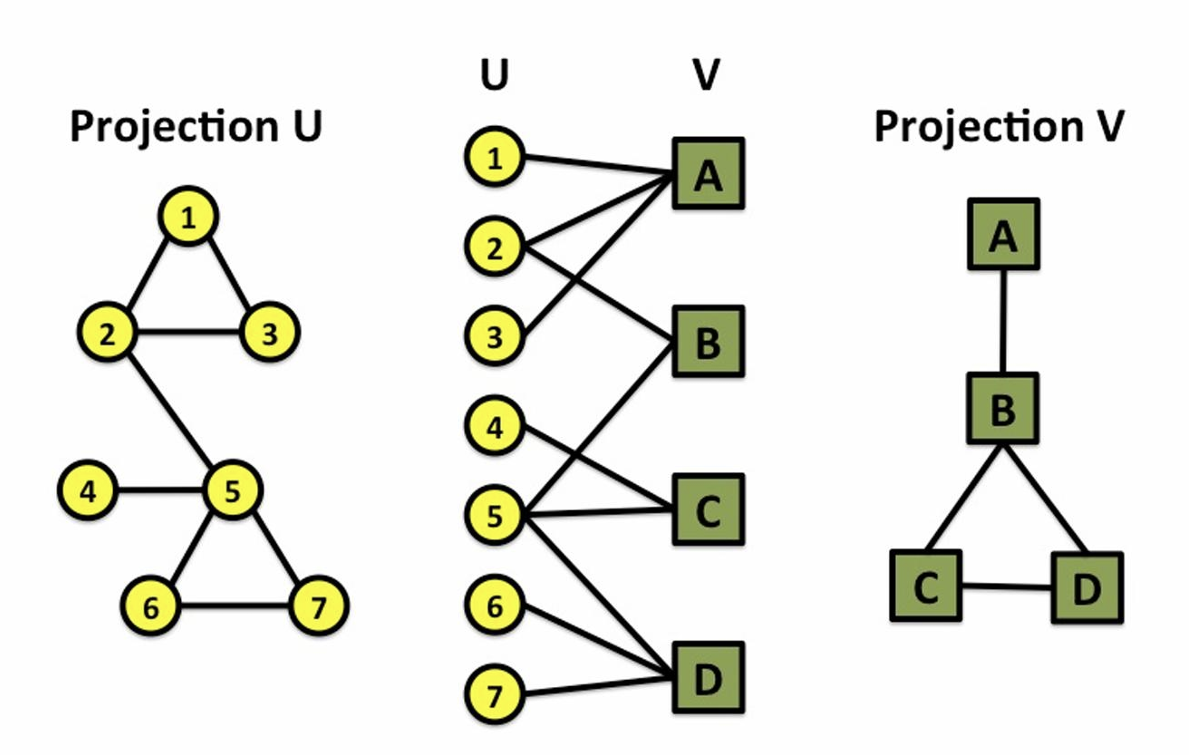
• Bipartite Graph: two disjoint sets U - V 다 서로 연결됨
• Folded/Projected Bipartite Graph: Author collaboration networks, Movie co-rating networks

• Tree: All nodes are connected, No cycles

Representing Graphs

• Adjacency Matrix

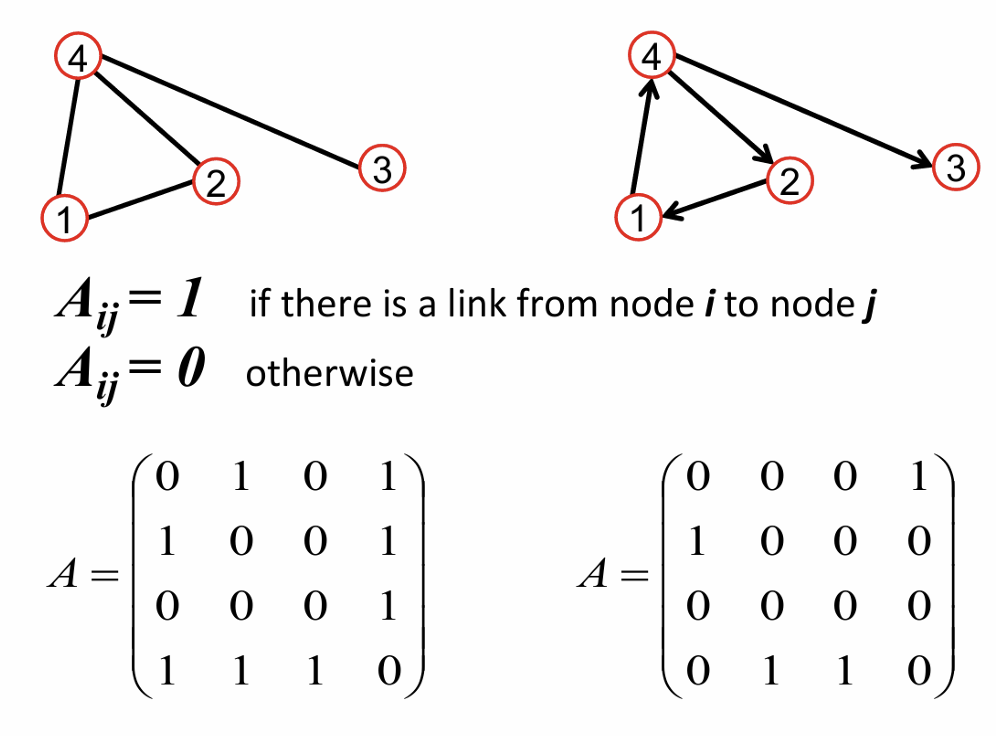
• Unweighted, Weighted, Self-edges, Multigraph
  real-world networks are sparse

• Alternatives: Edge List: set of edges
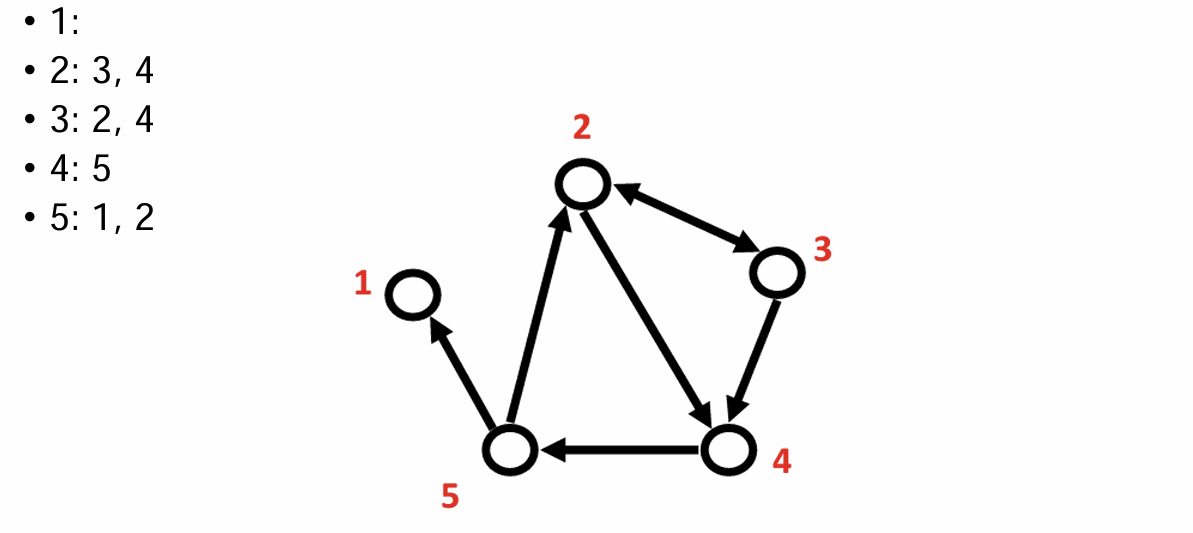
• Adjacency List: all neighbors of node

Modeling a Network with Graph
target object - node
relation, want to represent - edges

Week 2-1. Graph Properties

1. Network Properties

coarse-grained characteristics: 거친 입자 특성
Network Properties: Degree Distribution
P(k): Probability that a randomly chosen node has degree k
$N_k$ = # nodes with degree k
$\displaystyle P(k) = \frac{N_k}{N}$

Paths in a Graph
A path is a sequence of nodes in which each node is linked
to the next one
$P_n = {i_0,i_1,...i_n}, P_n = {(i_0,i_1),(i_1,i_2),...,(i_{n-1},i_n)}$

Network Properties: Distance(Shortest Path Length)
The number of edges along the shortest path connecting the nodes
• If the two nodes are not connected, the distance is usually defined as infinite (or zero)

Network Properties: Diameter & APL
• Diameter: The maximum (shortest path) distance between any pair of nodes in a graph
• Average path length (for a connected graph or a strongly connected directed graph)

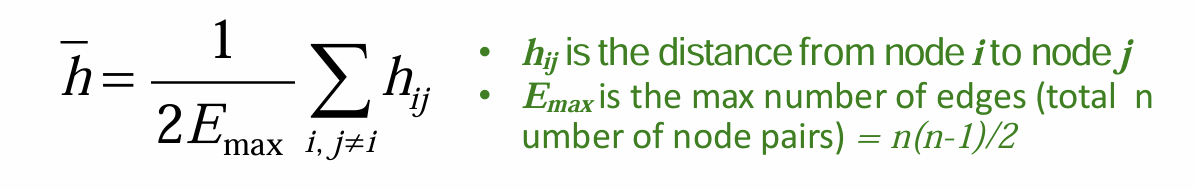
+isolated nodes are not considered

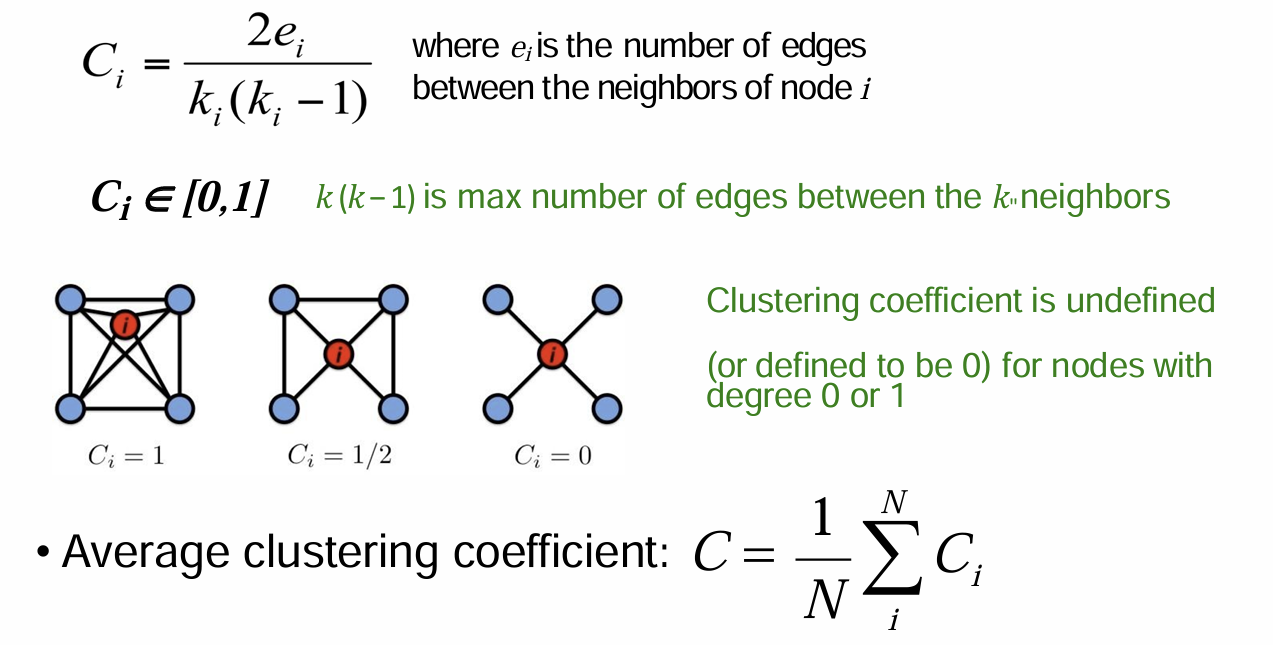
Network Properties: Clustering Coefficient
for undirected graphs
• How connected are $i$’s neighbors to each other? 이웃끼리 얼마나 연결돼있는지, 이웃들이 연결돼있을수록 1에 가까움, 연결 없으면 0
• Node i with degree $k_i$

Network Properties: Connectivity
Size of the largest connected component
• Largest set where any two vertices can be joined by a path
Finding connected components: BFS, find unvisited node and BFS

2. Network Properties in Real-world Networks

Example: MSN Messenger
p13 week2

Week 2-2. Random Graph Generation & Small World

1. Generating Random Graph(Erdos-Renyi)

Random Graph Model
$G_{np}$: undirected graph on n nodes where each edge (u, v)
appears i.i.d. with probability p

• Degree Distribution

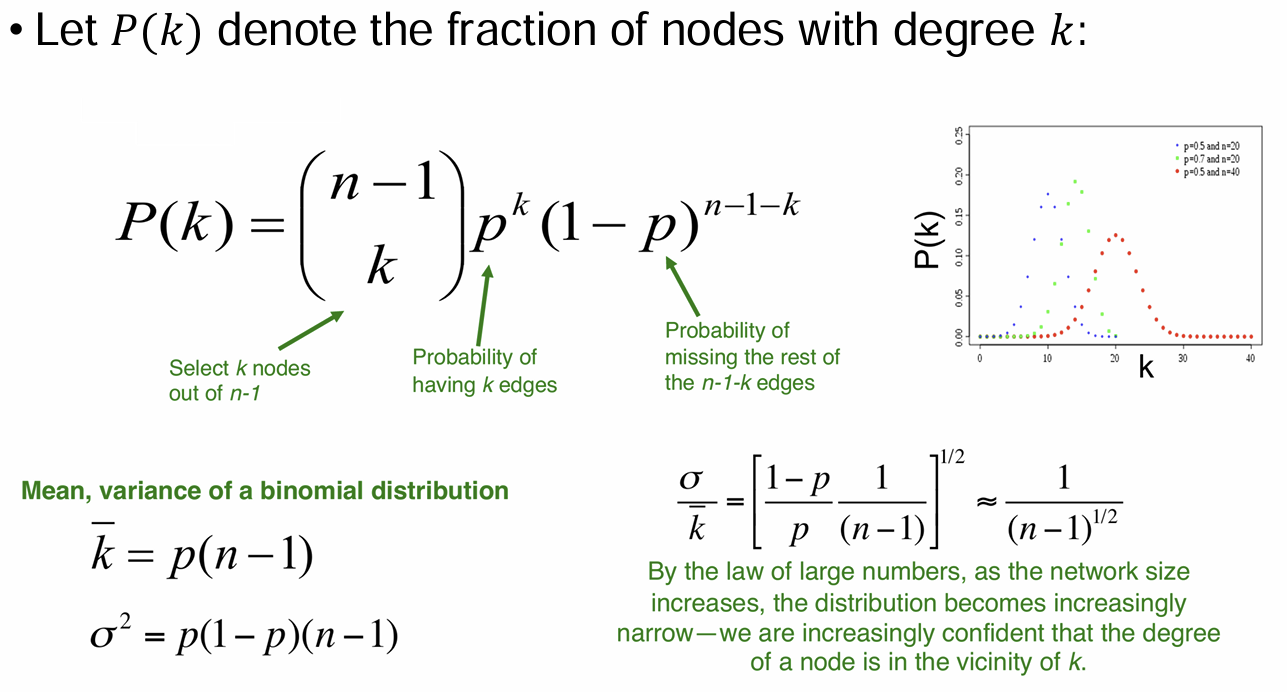
binomial: 이항식

• Clustering Coefficient of $G_{np}$
  i.i.i, prob p

Ref) Definition of Expansion

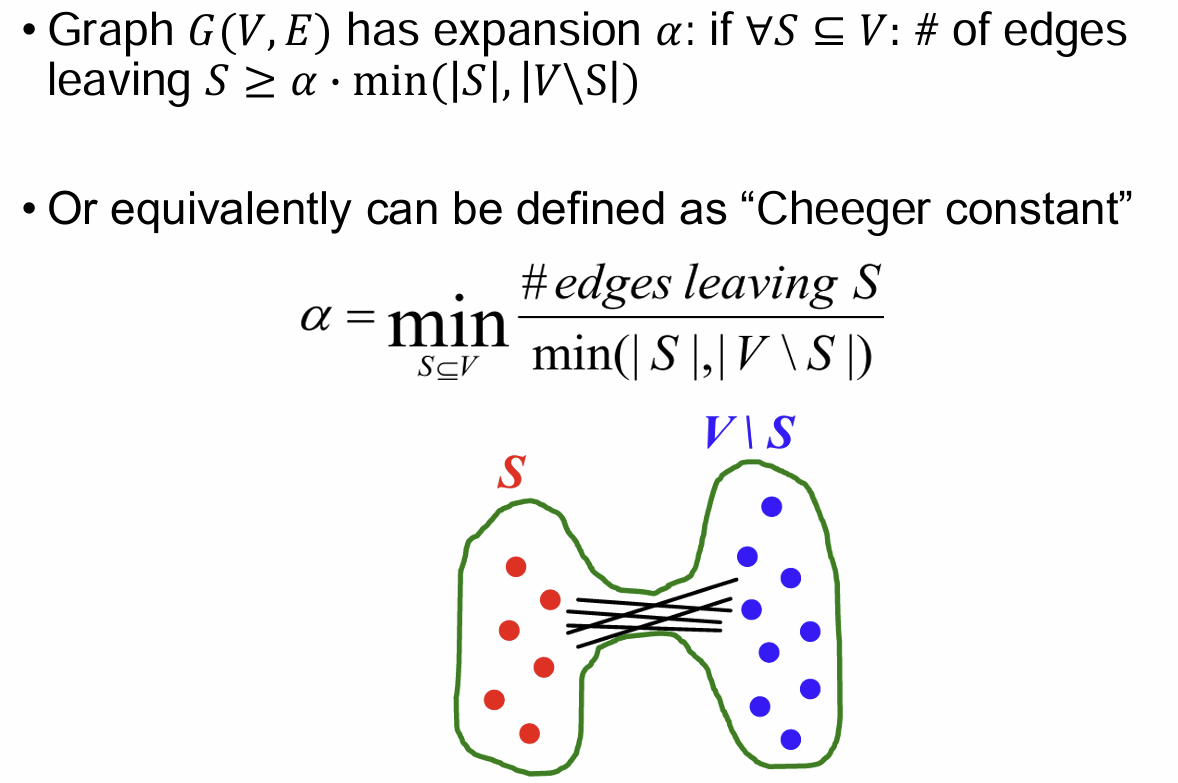
• Expansion in Random Graphs
  logarthmic number of steps for BFS to visit all nodes

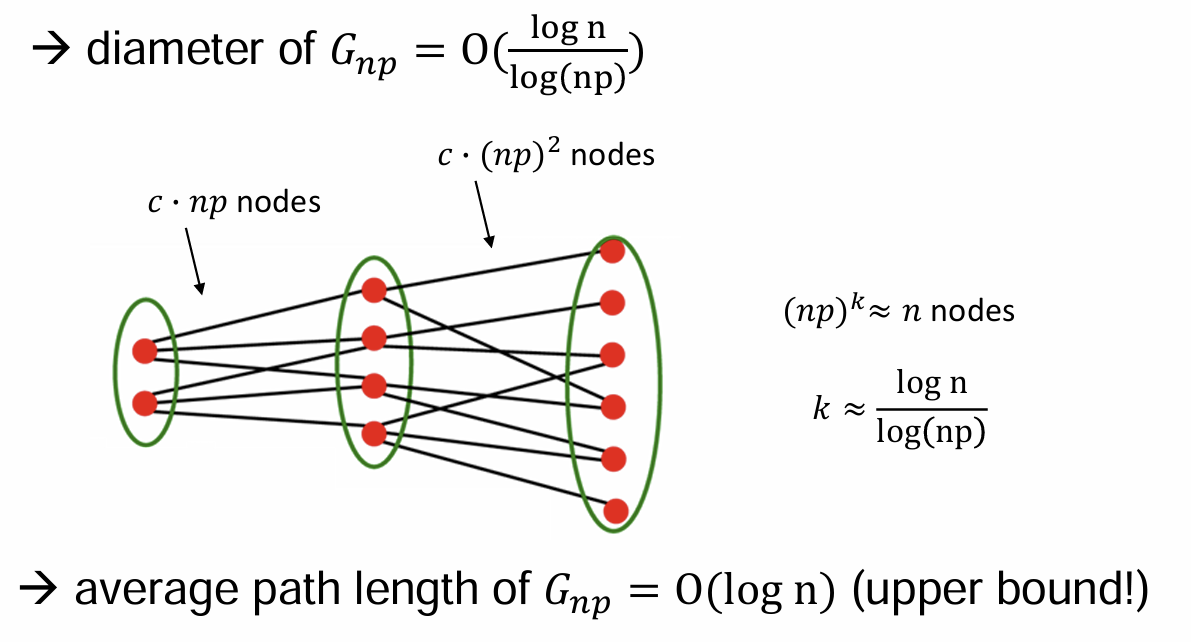
• Evolution of a Random Graph
  Real-world Networks vs. $G_{np}$

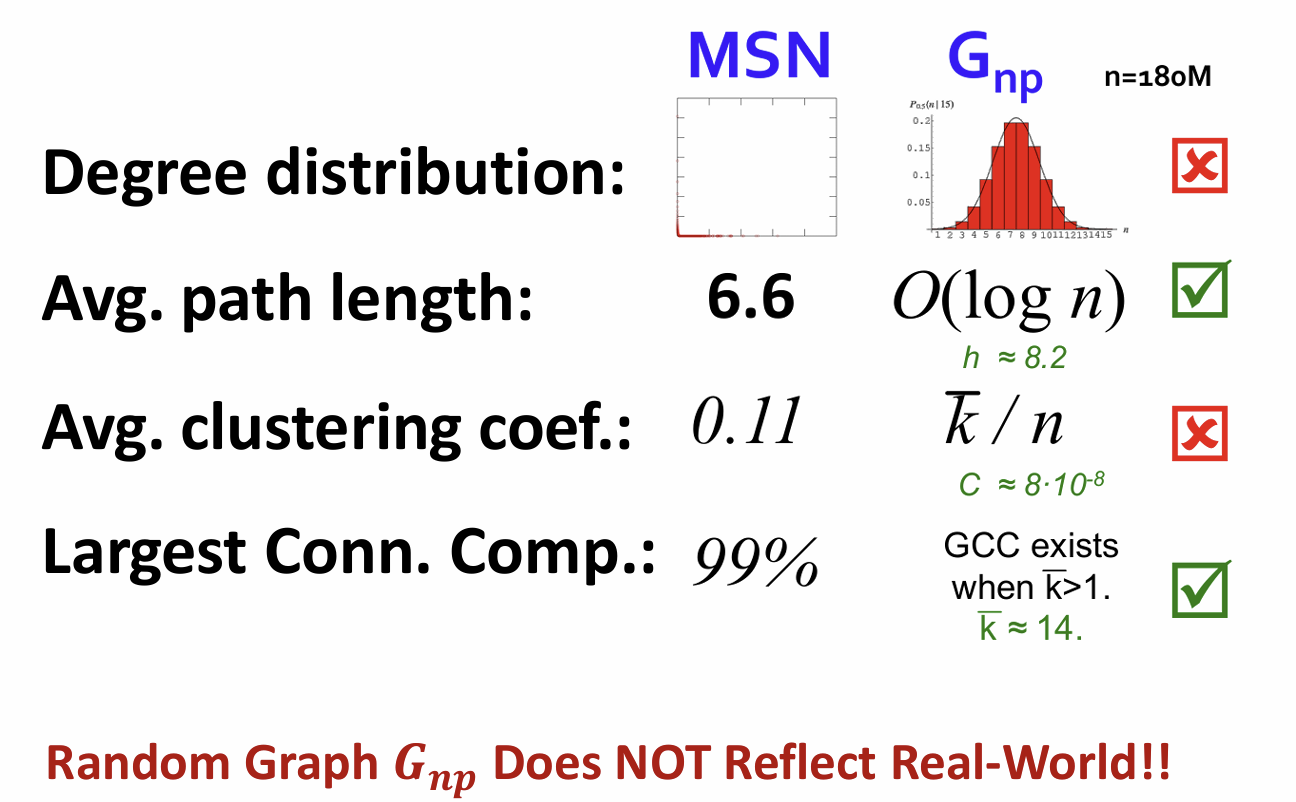
2. The Small-World Model

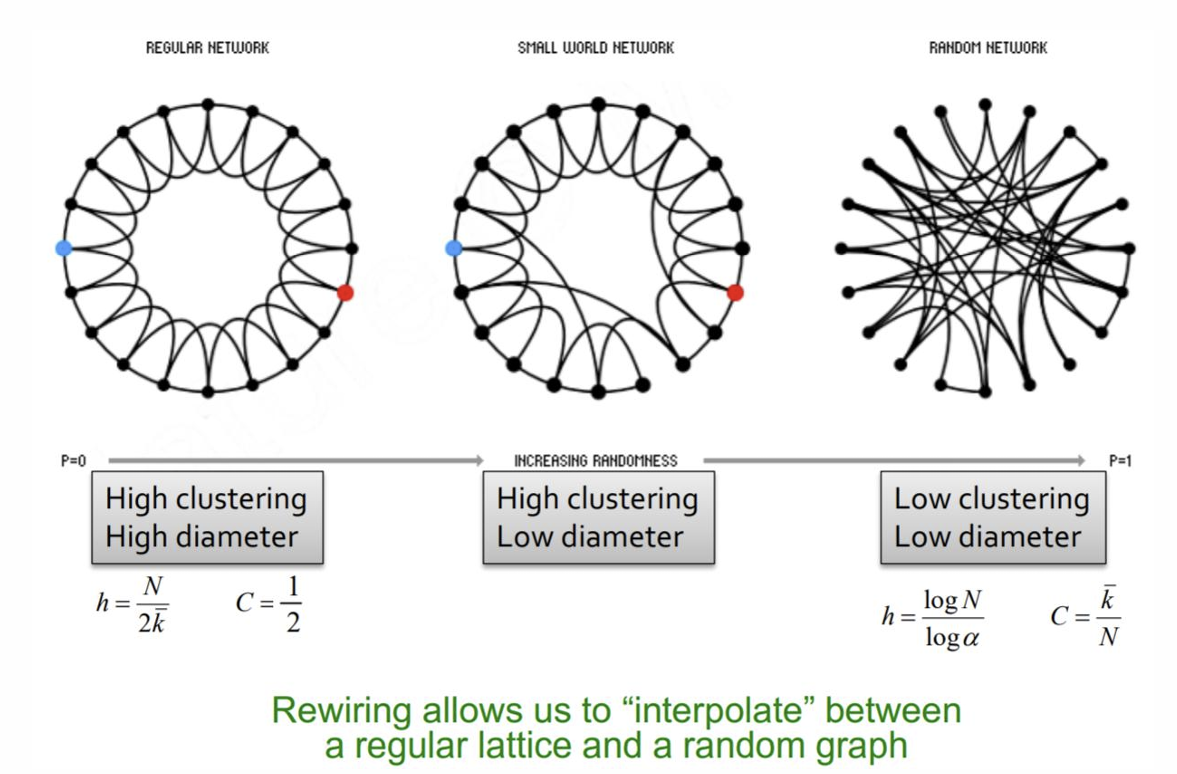
Solution: The Small World Model
Start with a low-dimensional regular lattice with high clustering coefficient
introduce randomness: add/remove edges to create shortcuts to join remote parts
lattice: 격자
regular high diameter - random low diameter

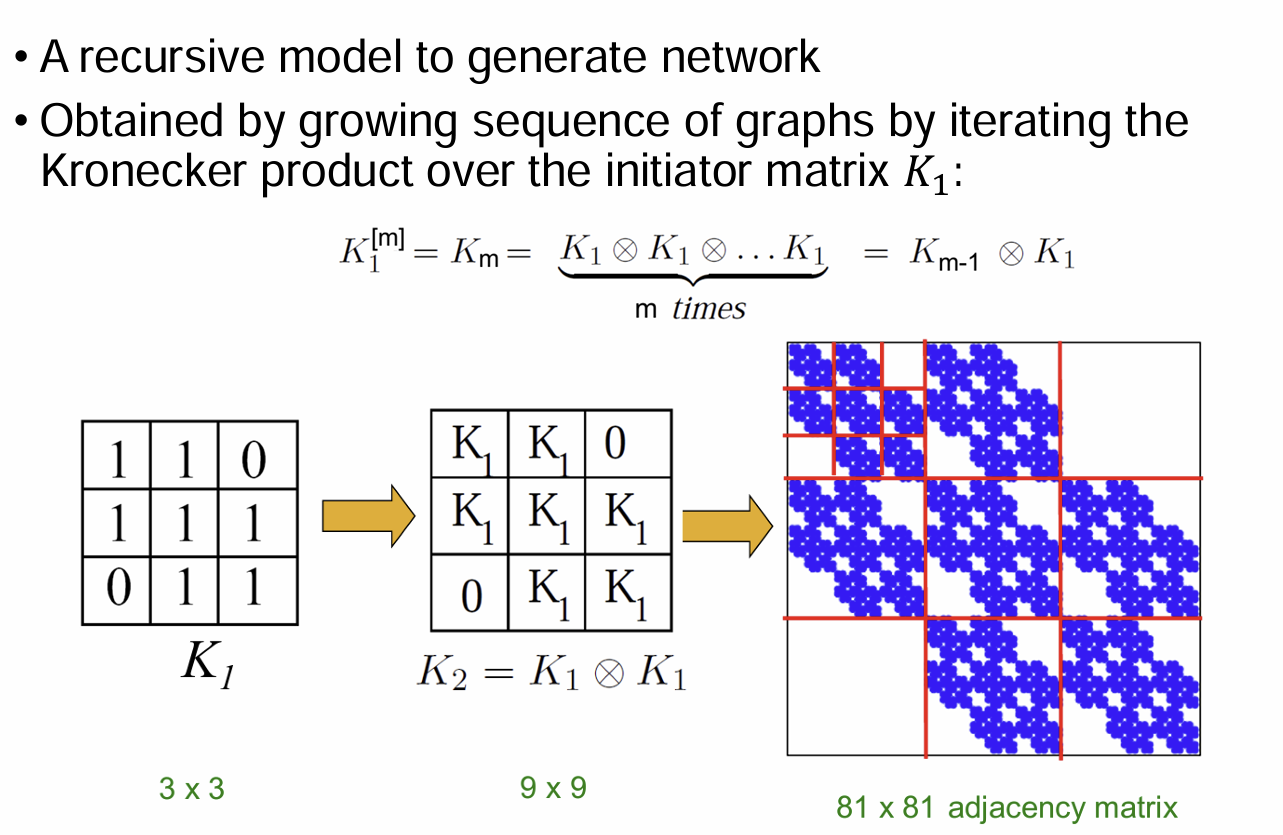
3. Kronecker Graph Model

Idea: Recursive Graph Generation
Self-similarity
Ref.) Definition of Kronecker Product

• Stochastic Kronecker Graph