[ML] 5. Deep Learning (CNNs)

Lecture Week 9-1. Deep Learning (CNNs)

background

1. Discrete (digital) convolution

내부 계산
: used to smooth or sharpen an image, comprises "sum-of-products" and "shift" operation

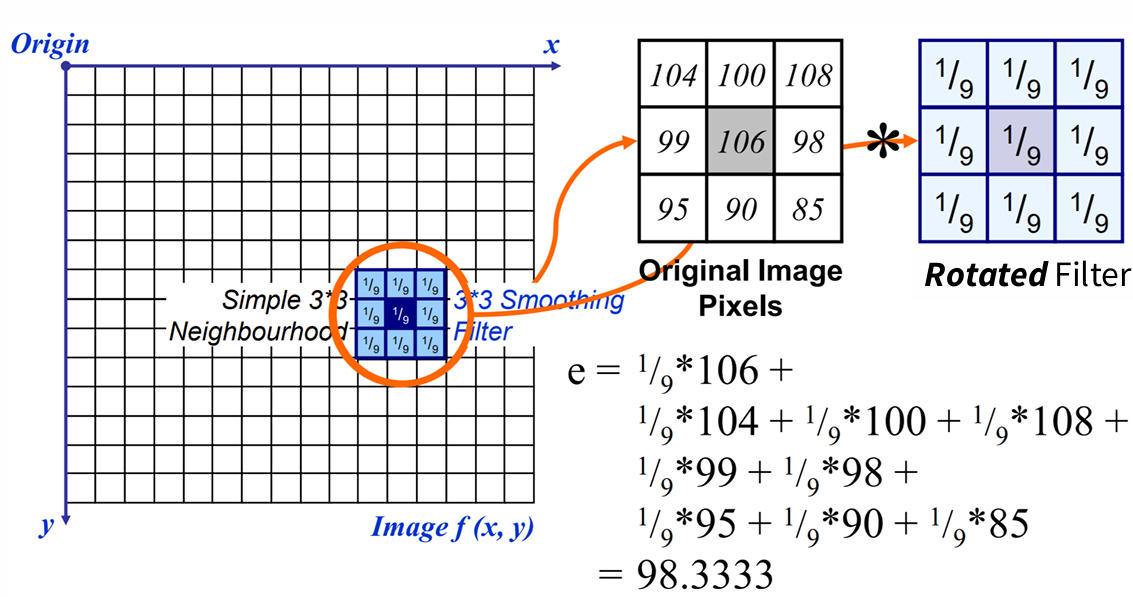
Smoothing operation

• mean filter
  :average all of the pixels in the neighborhood, mean of its neighbors
  removing noise, highlighting gross detail(철저한)

• Sobel edge detector
  detect gradients, sudden changes in brightness, edges

실습 사이트: http://setosa.io/ev/image-kernels/

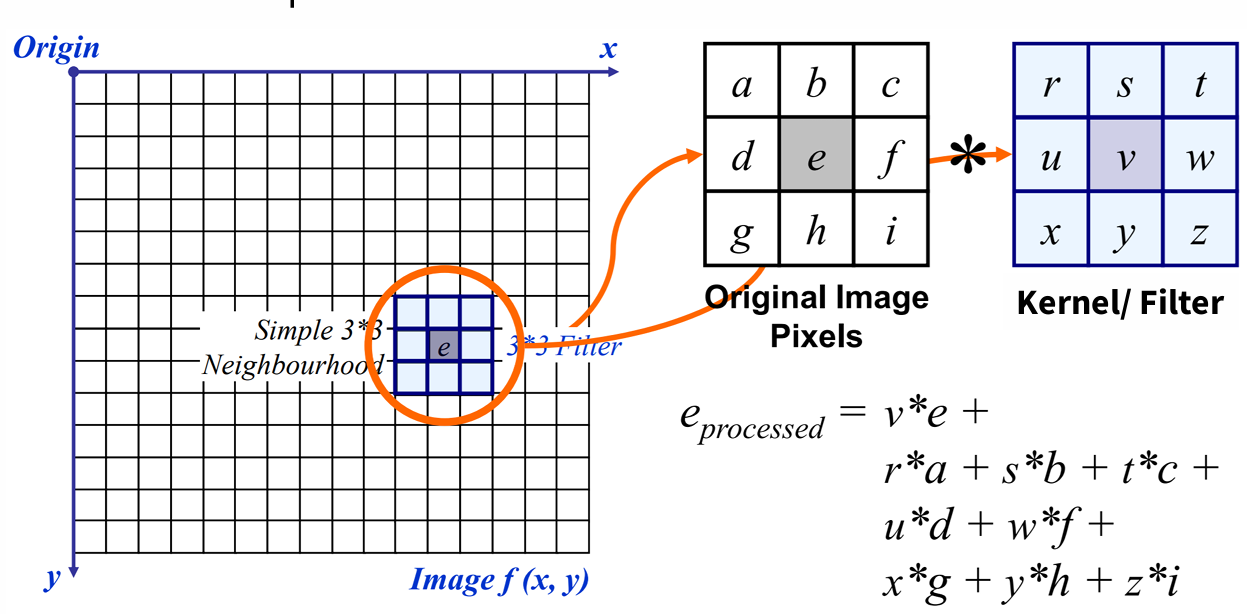
Convolution: pick 3x3 matrix k of weights, slide this over an image, compute inner product(similarity) of k and the corresponding field of the image, and replace the pixel in the center of the field with the output of the inner product operation
convolution extract low-level "features" from an image
varing the weights of k; parameters
used for edge detection, blurring, sharpening, etc.

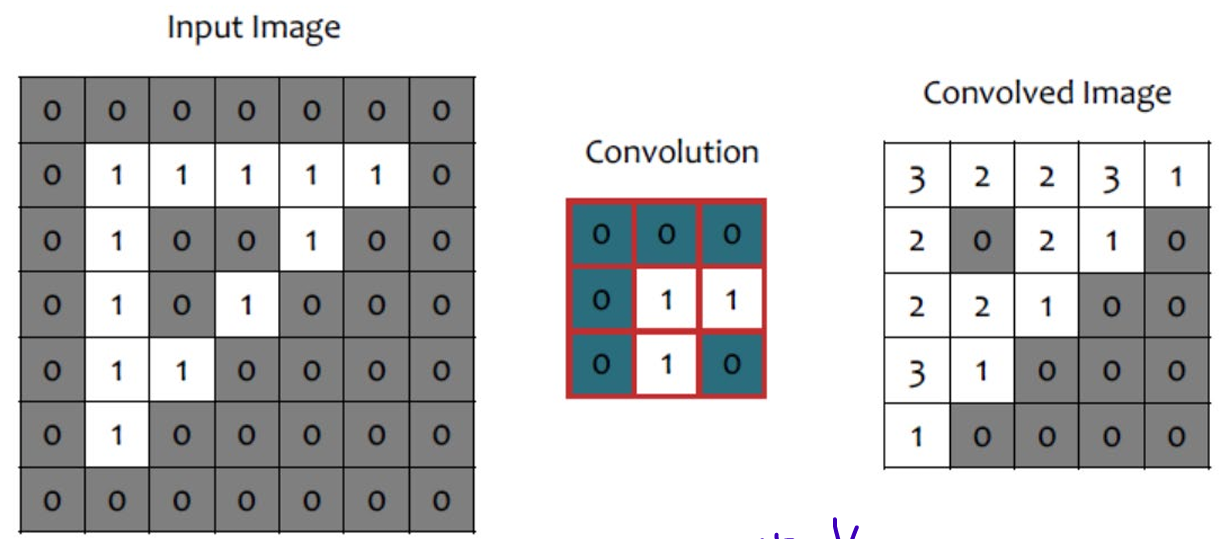
2. Convolutional Neural Nets: Stride, Pooling, Padding

1. Stride
: skip some of the slide. Downsampling with Stride
A stride of 3 means skipping every 2 slides, downsizing roughly by factor 3.

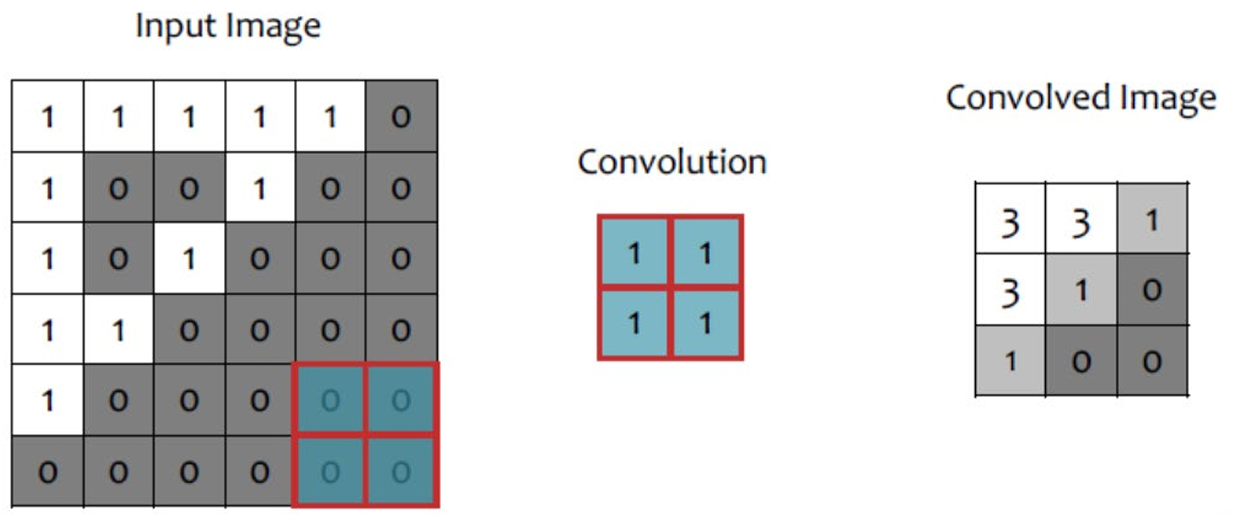
2. Pooling

• Average-Pooling

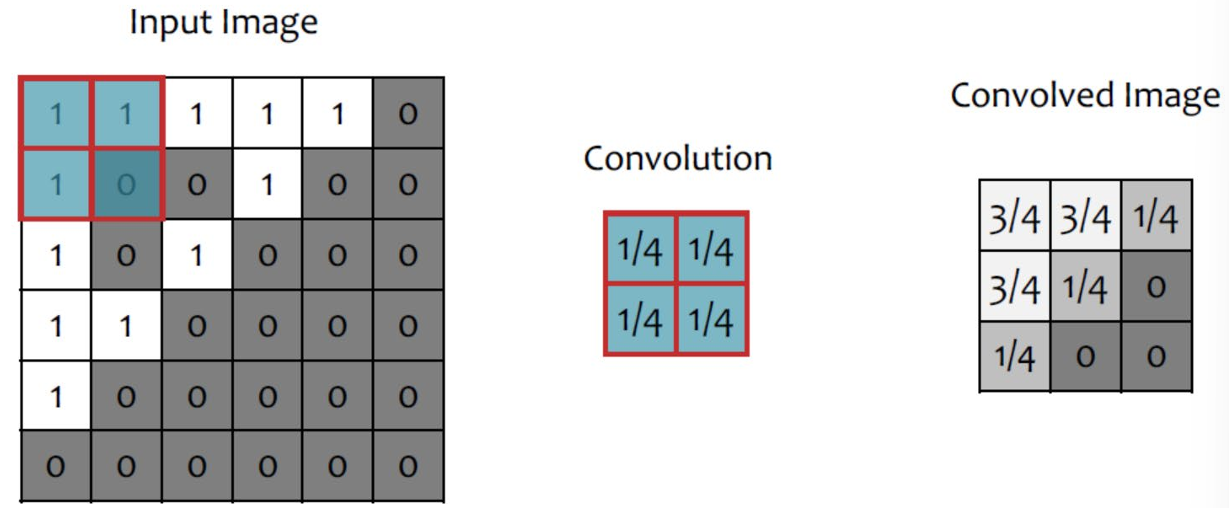
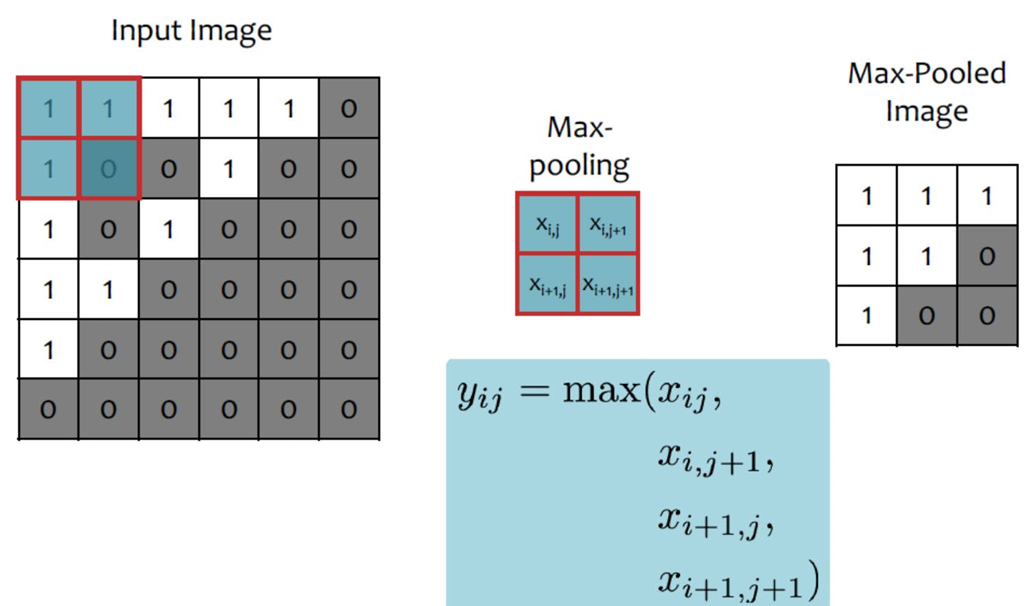
• Max-Pooling

3. Padding
: put the edges with extra, fake pixels

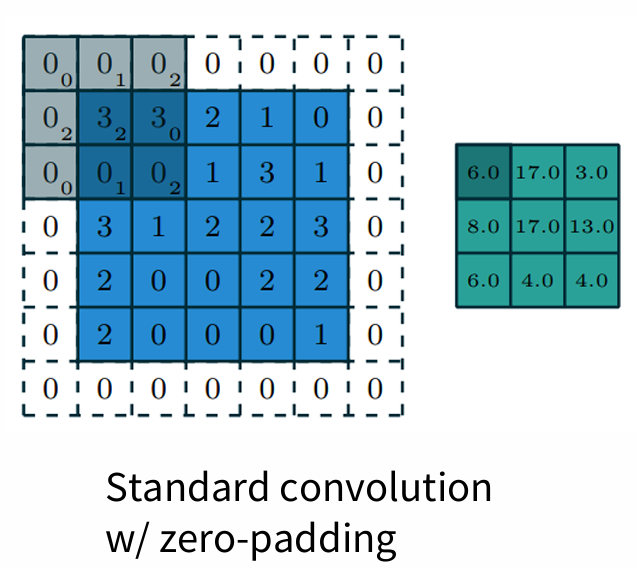
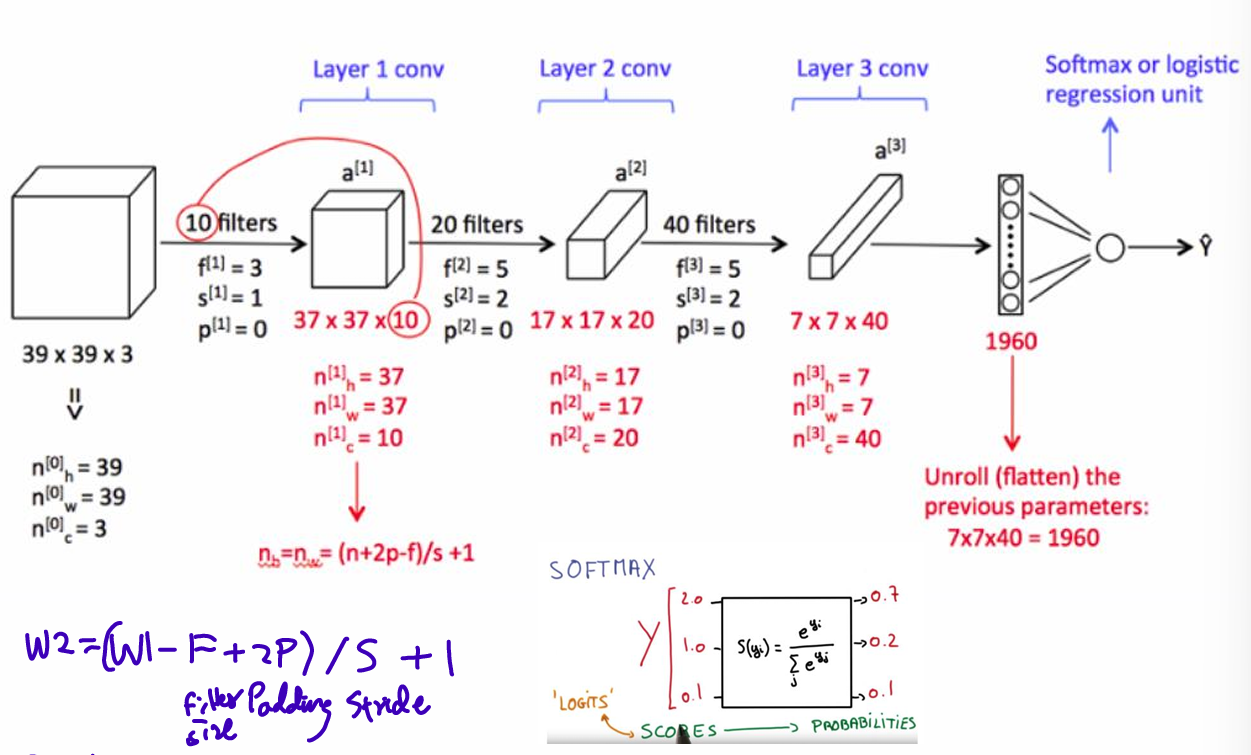
3. CNN: 3d Kernel, multiple filters

RGB color 3-dimensional
input W1 x H1 x D1
hyperparameters;
number of filters K, filters' spatial extent F, the stride S, the amount of zero padding P
produce W2 x H2 x D2
W2 = (W1 - F + 2P) / S + 1
H2= (H1 - F + 2P) / S + 1
D2 = K
total parameters(weights + biases): F$^2$ D1 K + K

Why convolutions?

• Parameter sharing: parameter saving, a feature detector is also useful in another part of the image

• Sparsity of connections: each output value depends only on a small number of inputs

• Structure preservation

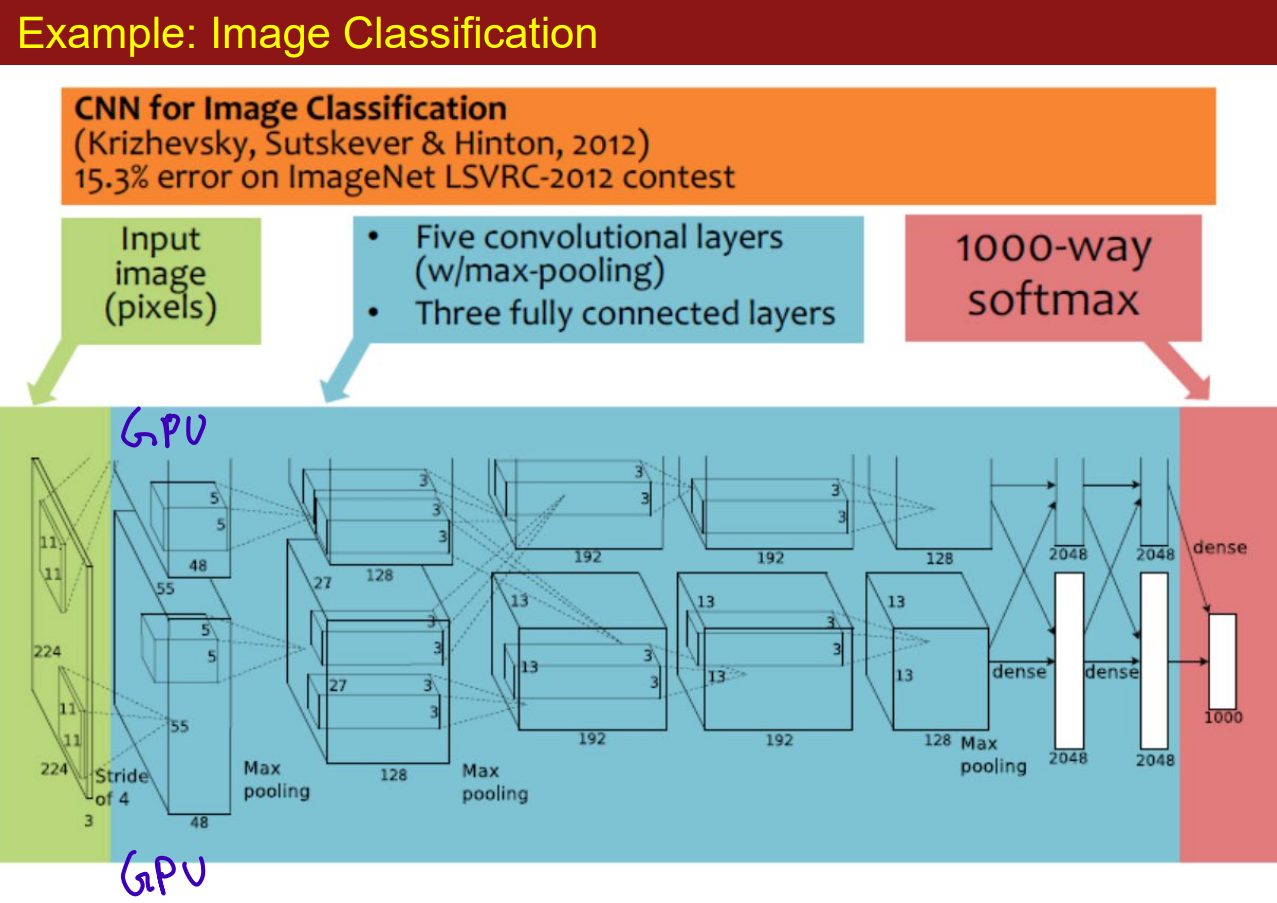
• example

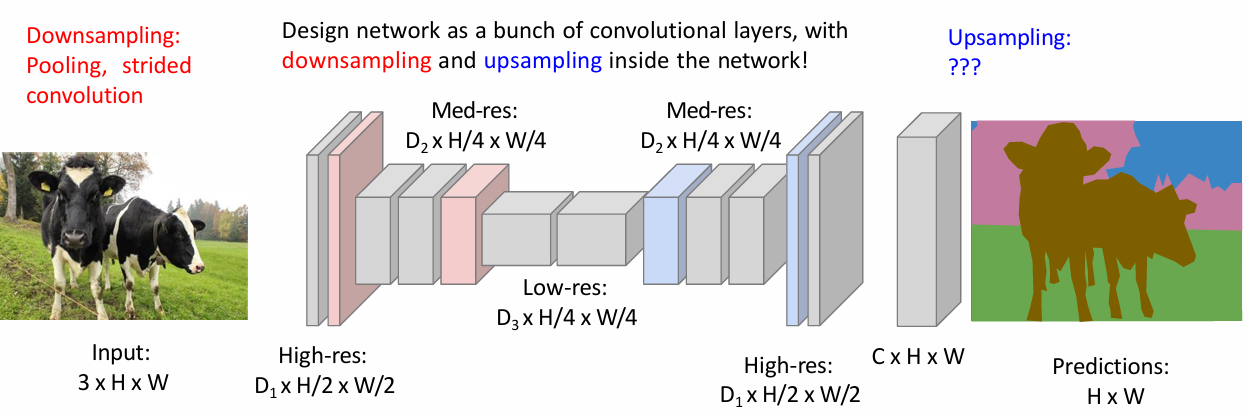
4. CNN: Upsampling

Semantic Segmentation Idea
: fully convolutional

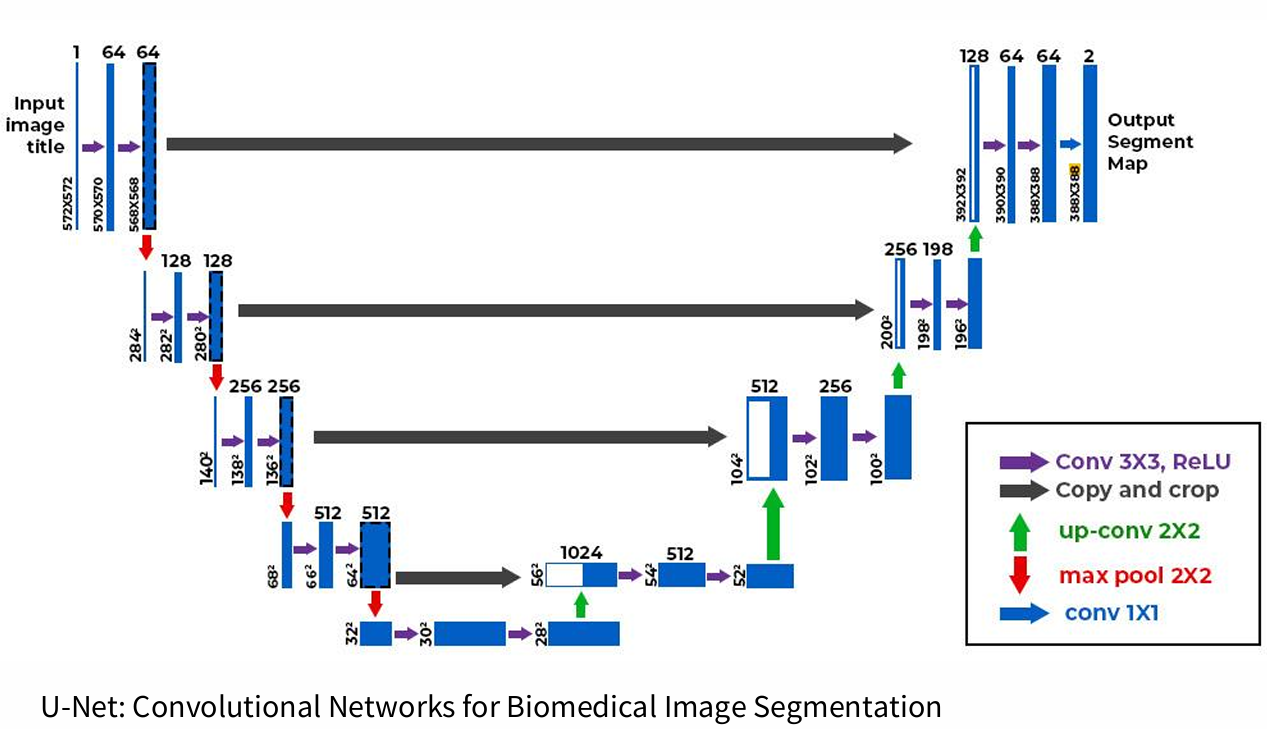
Unet: convolutional networks for Biomedical Image Segmentation

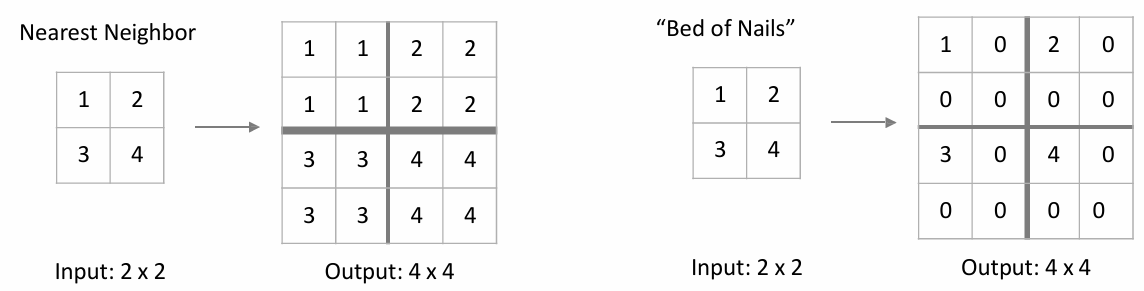
In-Network upsampling: Unpooling
Nearest Neighbor/ Bed of Nails

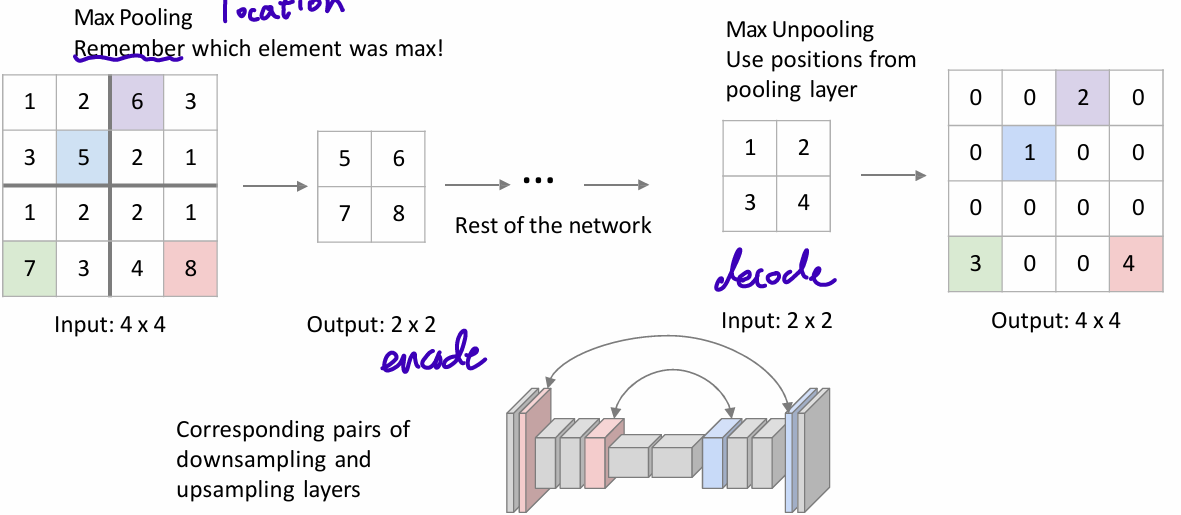
Max Unpooling
no learning process; not optimal, not using data

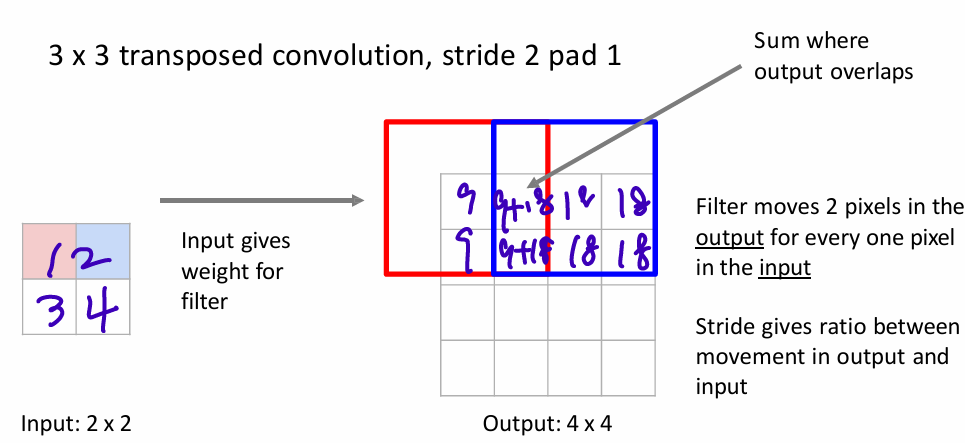
Learnable Upsampling: Transposed Convolution

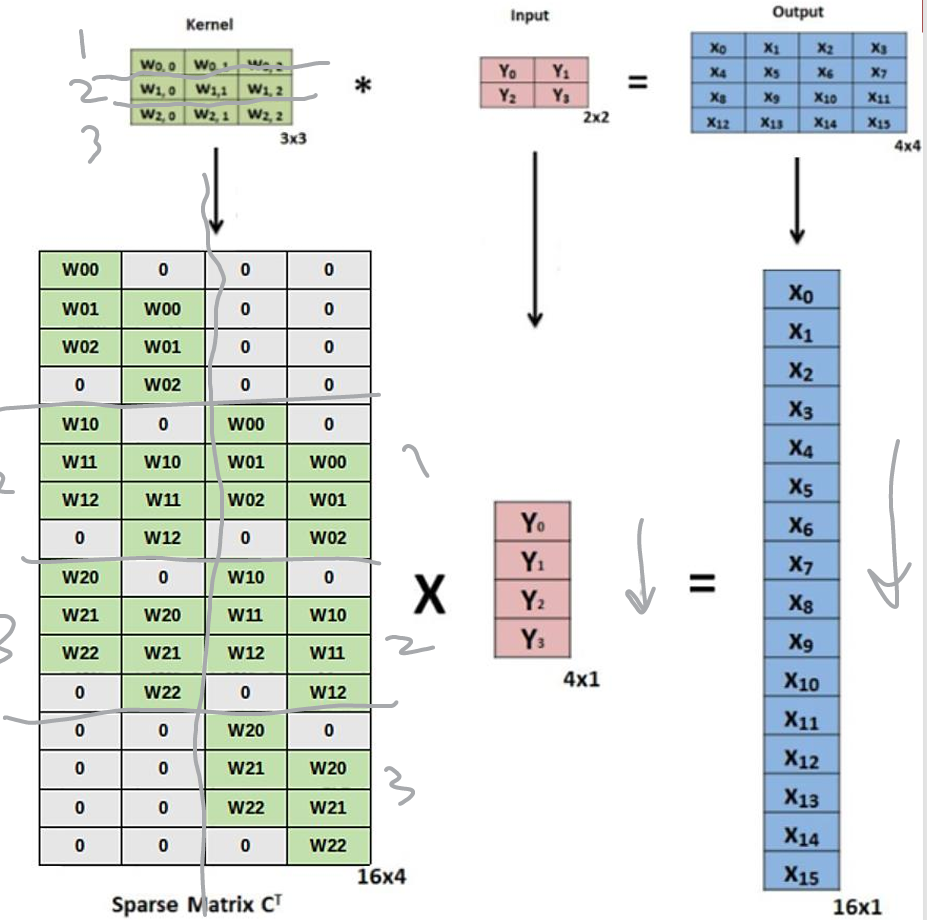
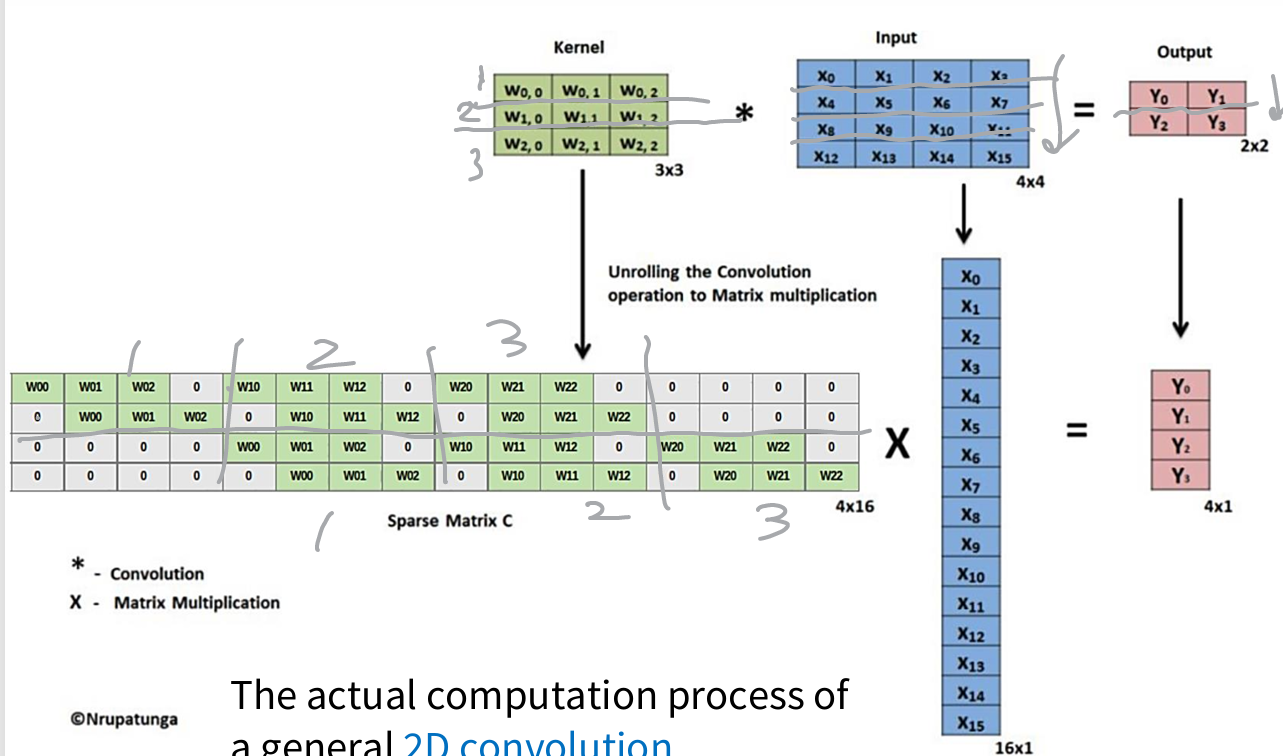
5. Convolution as Matrix Multiplication

• 1D Example

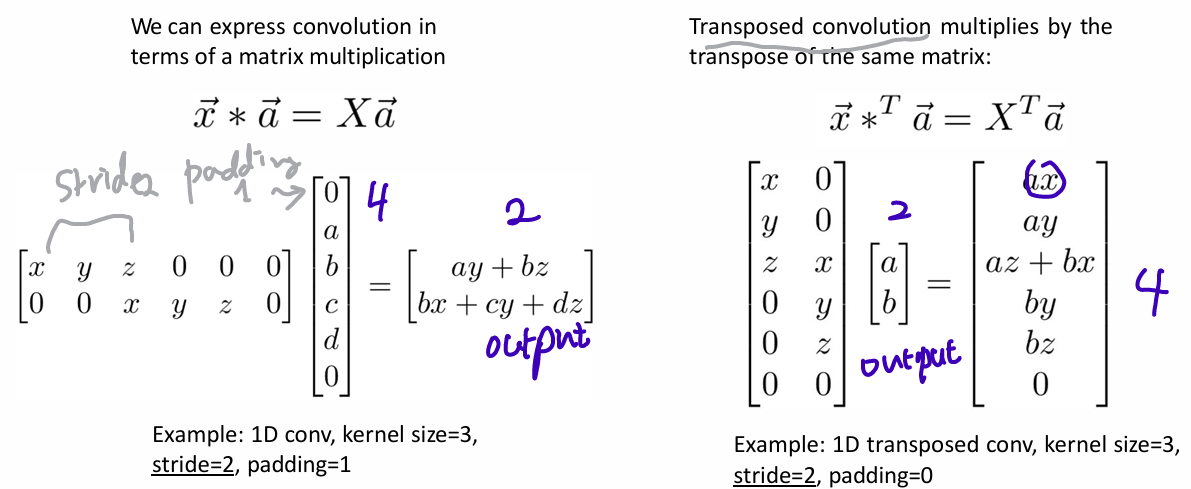
• 2D Example
  The actual computation process of a general 2D convolution
  ;stride 1, padding 0, kernel 3x3

The actual computation process of a 2D Transpose Convolution