[ML] 6. Support Vector Machine (SVM)

Week 10-1. SVM (Support Vector Machine)

Theory and Intuition: Hyperplanes and Margins

Hyperplane
: a flat subspace (N-1 dimension) that divides a higher dimensional space (N dimension)into two parts
create seperation between classes
when new point, use hyperplanes to assign a class
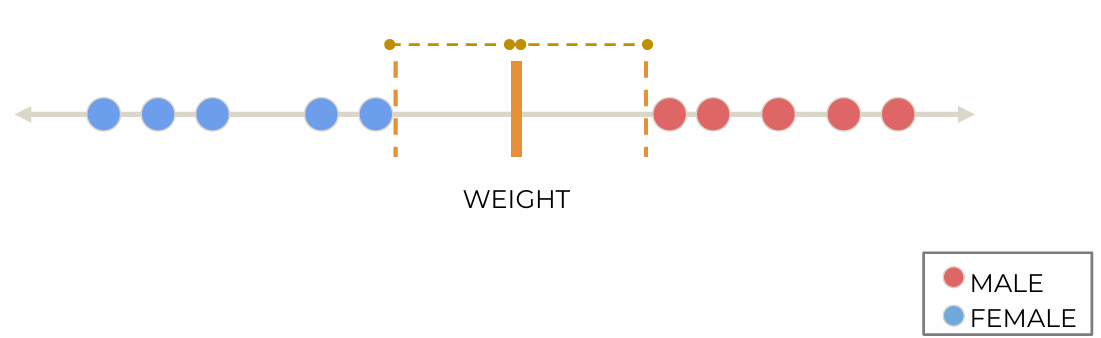
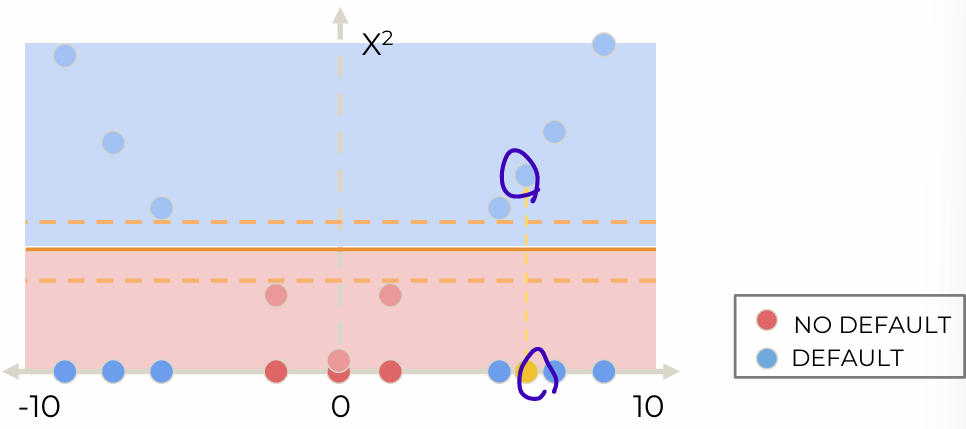
Example: a dataset with one feature, one binary target label
create seperating hyperplane
maximize the margin(여백) between the classes; maximal margin classifier

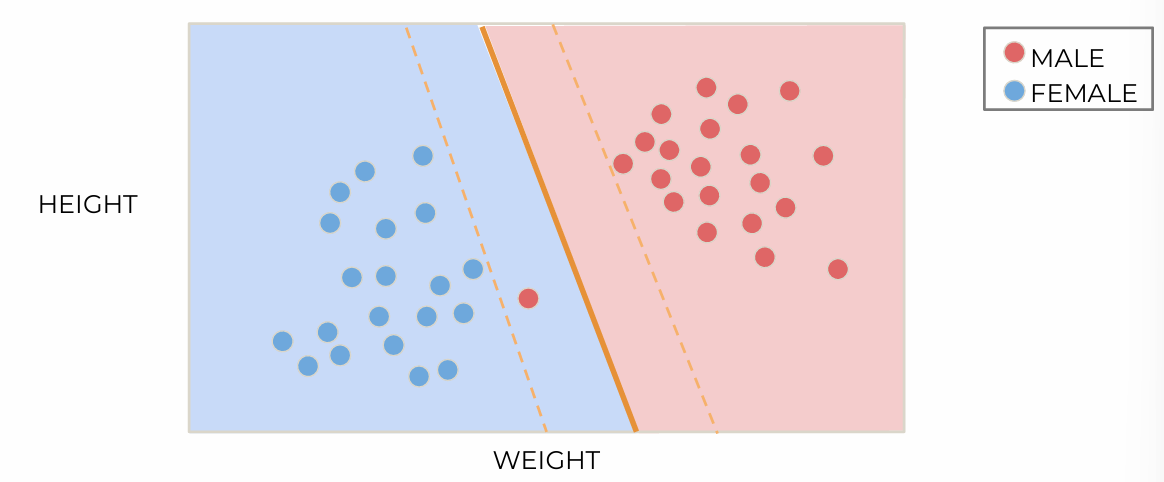
2D data, support vector

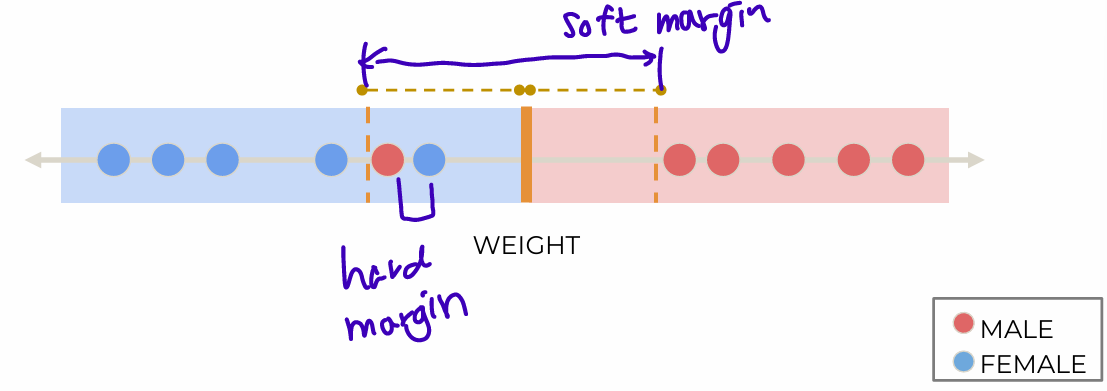
• Not perfectly seperable: misclassification exists
  Bias-variance trade-off
  variance: overfitting, bias: underfitting
• soft margin

Cross validation to determine the optimal size of the margin

Theory and Intuition: Kernels

When hyperplane performs poorly, move from Support Vector Classifier to Support Vector Machines
Kernels are used to project the features to a higher dimension

• Kernel Projection 1D

Mathematics

• Linear classifier: finding optimal solution
  • Maximizes the distance between the hyperplane and the “difficult points” close to decision boundary
  • One intuition: if there are no points near the decision surface, then there are no very uncertain classification decisions
  equation of n-dimensional hyperplane: $w_1 x_1 + w_2 x_2 + w_3 x_3 + ... + w_n x_n = a => \vec{w}^T \vec{x}$

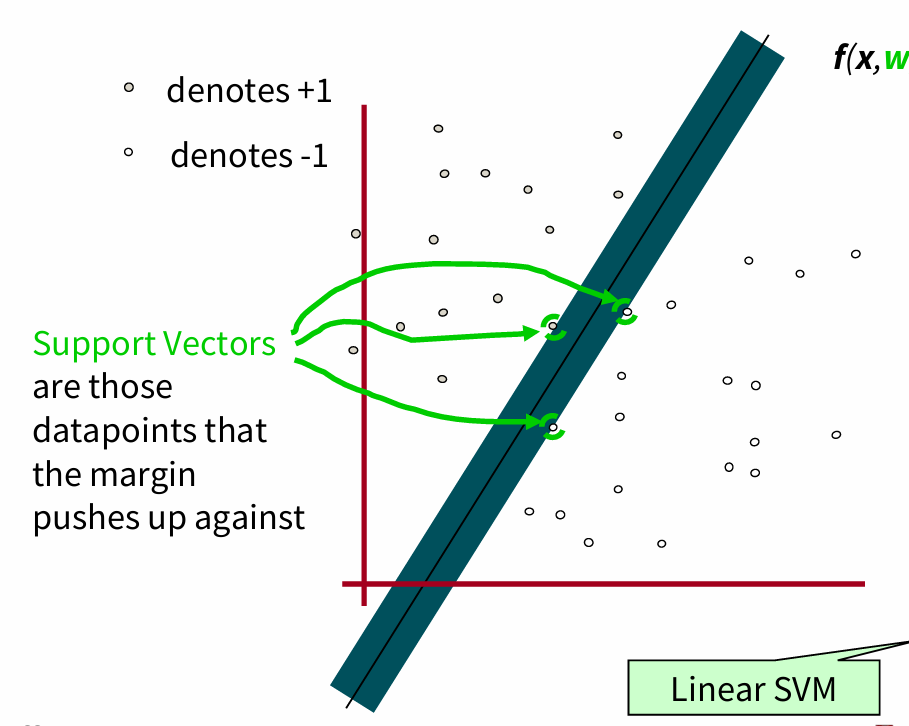
Support Vectors: Intuition
:traing data points closer to the border which are most crucial to design the classifier
To chose a good line: optimize some objective function
Primarily we want least number of misclassification of test points, points closer to boundary more likely to be misclassified

Support Vector Machine(SVM)
:maximum margin classifier
$L_1, L_2$ are lines defined by the support vectors
margin: seperation between the lines
The decision boundary is the line that pass through the middle of $L_1$ and $L_2$.

• another intuition: fat seperator between class, less choices, decreased capacity of the model

Linear Classifiers
f(x, w, b) = sign(wx - b)
Define the margin of a linear classifier as the width that the boundary could be increased by before hitting a datapoint.
Maximum margin linear classifier(LSVM)

Large-margin Decision Boundary
Recall: the distance from the point (m, n) to the line Ax + By + C = 0:
$\displaystyle d = \frac{|Am + Bn + C|}{\sqrt{A^2 + B^2}}$

The perpendicular distance(수직거리) of the line (L) from any point $\vec{u} = [u_1, u_2, u_3, ..., u_n]^T$: $\displaystyle d(\vec{u},L) = \frac{|\vec{w}^T \vec{u} - a|}{\parallel \vec{w}\parallel}$
The perpendicular distance of the line from origin: $\displaystyle d(0,L) = \frac{|a|}{\parallel \vec{w}\parallel}$

• minimize $||\vec{w}||^2 = \vec{w}^T\vec{w}$

• $y_i$ class label: (C1 class1, C2 class2)
  $y_i = \begin{cases}+1,\; \text{if}\; \vec{x_i}\in C_1 \\ -1,\; \text{if}\; \vec{x_i}\in C_2 \end{cases}$

• constraint to our optimization problem:
  $\vec{w}^T\vec{x_i}+b \leq -1, \;\forall \vec{x_i}\in C_2 \\ \vec{w}^T\vec{x_i}+b \geq 1, \;\forall \vec{x_i}\in C_1$
  class 2는 L1 아래쪽, class 1은 L2 위쪽

• simply say:
  $y_i(\vec{w}^T\vec{x_i}+b \geq 1\;\forall i\in {1,2,...,m})$
  (m: # of training samples)

Equation

• hyperplanes defined: $\beta_0 + \beta_1X_1 + \beta_2 X_2+...+\beta_pX_p = 0$
• Seperating Hyperplanes:
  $\beta_0 + \beta_1X_1 + \beta_2 X_2+...+\beta_pX_p > 0 \\ \beta_0 + \beta_1X_1 + \beta_2 X_2+...+\beta_pX_p < 0$
• Data Points:
  $x_1 = \begin{pmatrix}x_{11} \\.\\.\\.\\ x_{1p}\end{pmatrix},...,x_n = \begin{pmatrix}x_{n1} \\.\\.\\.\\ x_{np}\end{pmatrix}$

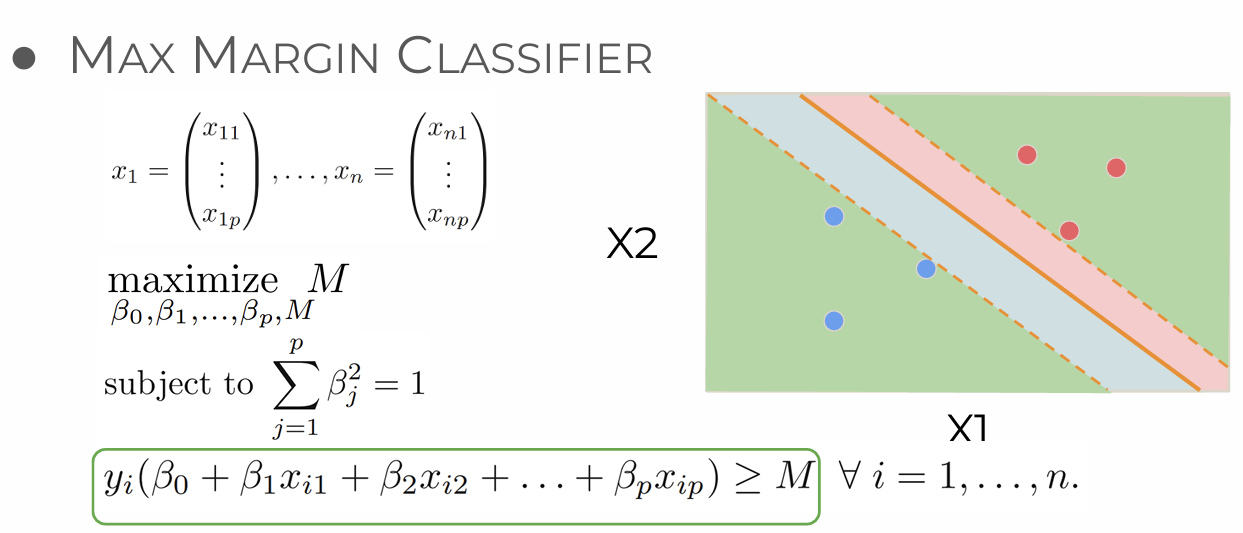
Hard Margin SVM Classifier (Max Marigin Classifier)

Soft Margin SVM Classifier (Support Vector Classifier)

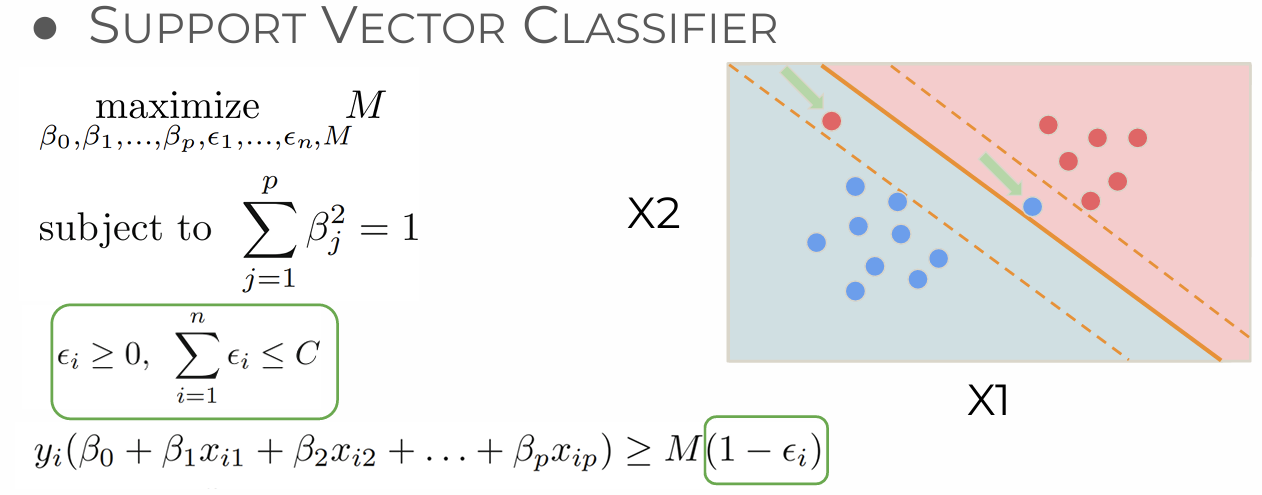
• C: Regularization parameter (user defined), Regularization inversely proportional to C, strictly positive, squared l2 penalty, default=1.0
  Small C; allows large $\epsilon_i$'s, more $\vec{x_i}$'s to slip through the margin (margin 안에 points 더 많아도 됨)
  Large C; forces small $\epsilon_i$'s
  c작으면 epsilon 작아짐, 더 다양한 경우- miss 많아짐

Kernel Trick
very large feature space
avoid computations in the enlarged feature space, only need to perform computations for each distinct pair of training points
The use of kernels can be a measure of similarity between the original feature space and enlarged feature space.
use inner(dot) product; similarty between the vectors

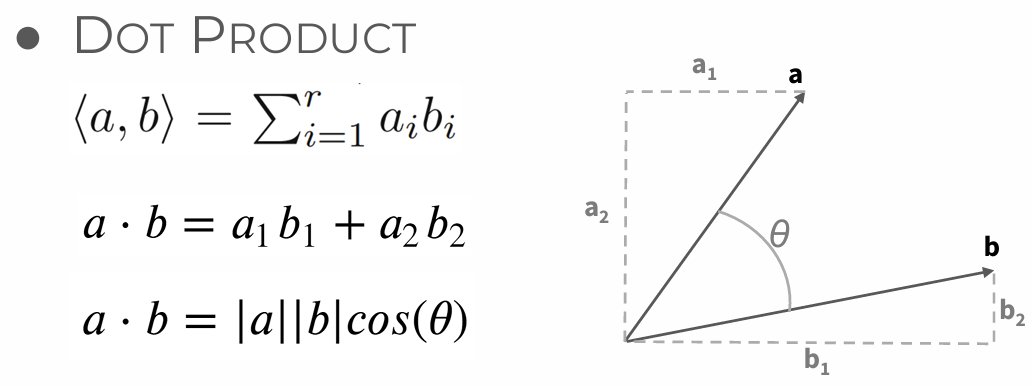
• Linear Support Vector Classifier rewritten
• (Linear) Kernel function

$\displaystyle f(x) = \beta_0 + \sum_{i\in S}\alpha_i K(x,x_i)$

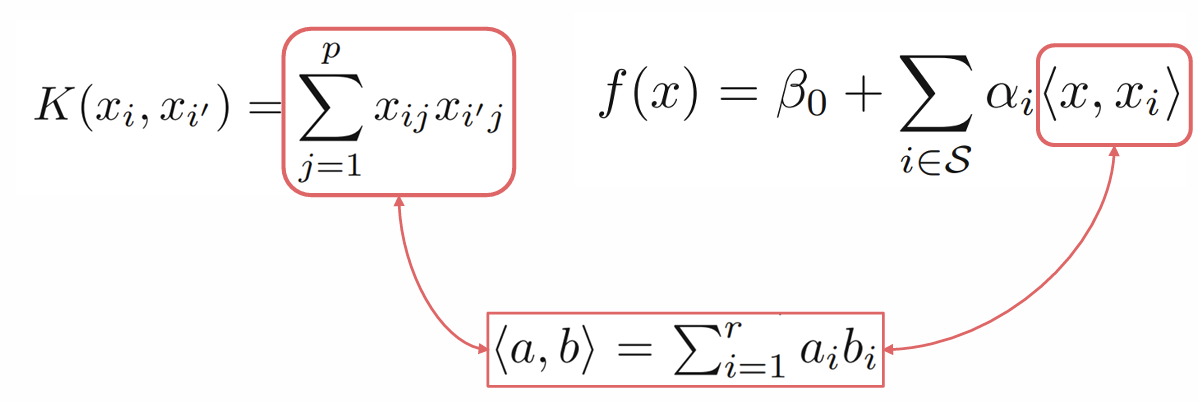
• Polynomial Kernel

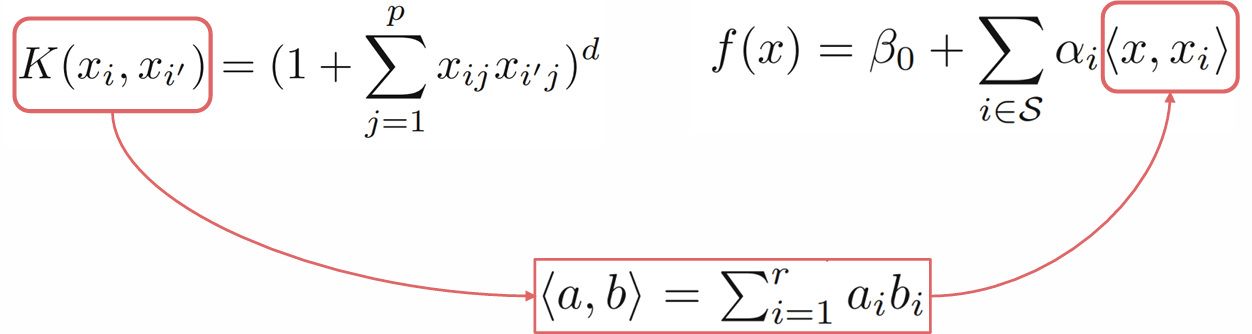
• Radial Basis Kernel

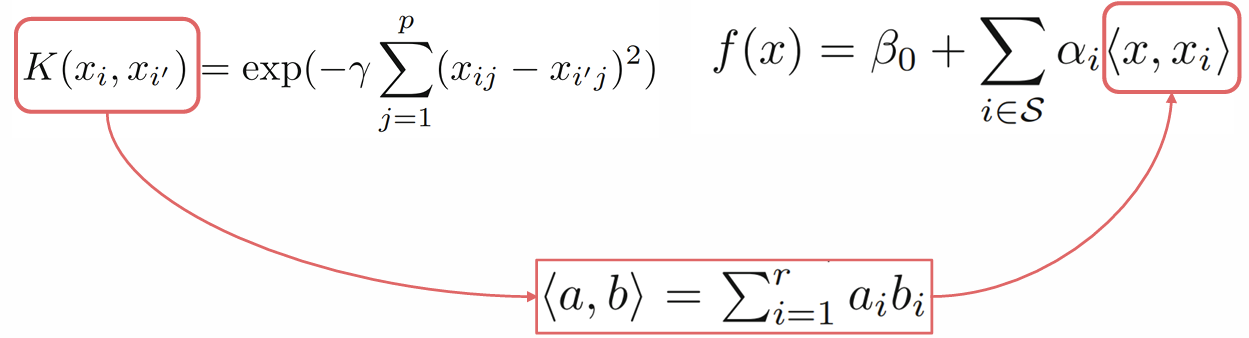
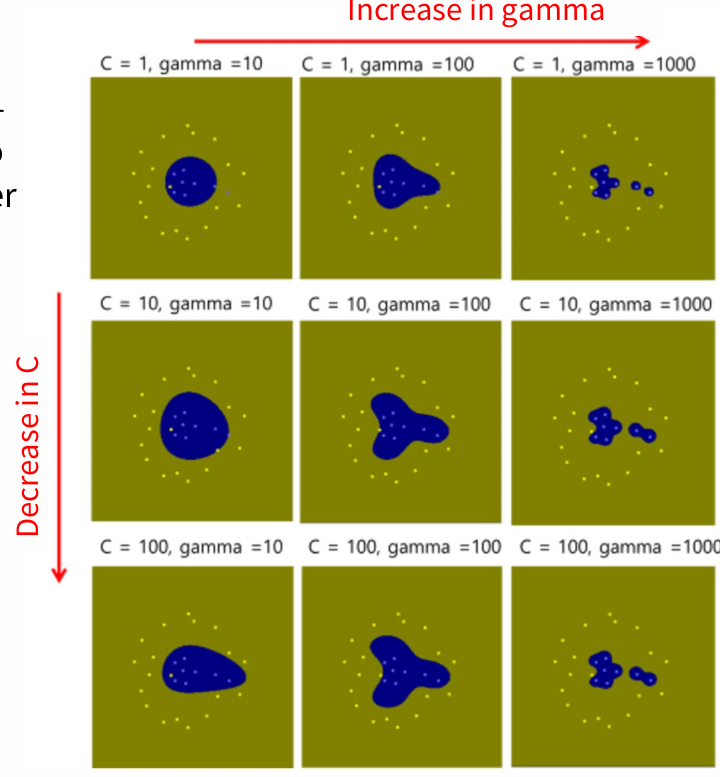
As gamma $\gamma$ increases, the influence range of a data point shortens, while a lower gamma extends it.