강의 보고 공부한 것을 정리하는 목적으로 작성된 글이므로 틀린 점이 있을 수 있음에 양해 부탁드립니다. (피드백 환영입니다)

우리가 앞에서 배운 Vector와 List는 1차적으로 나열된 형태를 표현하기 적합한 자료구조라고 볼 수 있다.
하지만 나중에는 이것만으로 부족한 상황이 나오게 될 것이다.

그래서 우리는 Tree를 배워볼 것이다!

트리란?

트리는 계층적 구조를 갖는 데이터를 표현하기 위한 자료구조라고 볼 수 있다.
노드(Node)는 데이터를 표현하고
간선(Edge)는 노드의 계층 구조를 표현하기 위해 사용한다.

예시

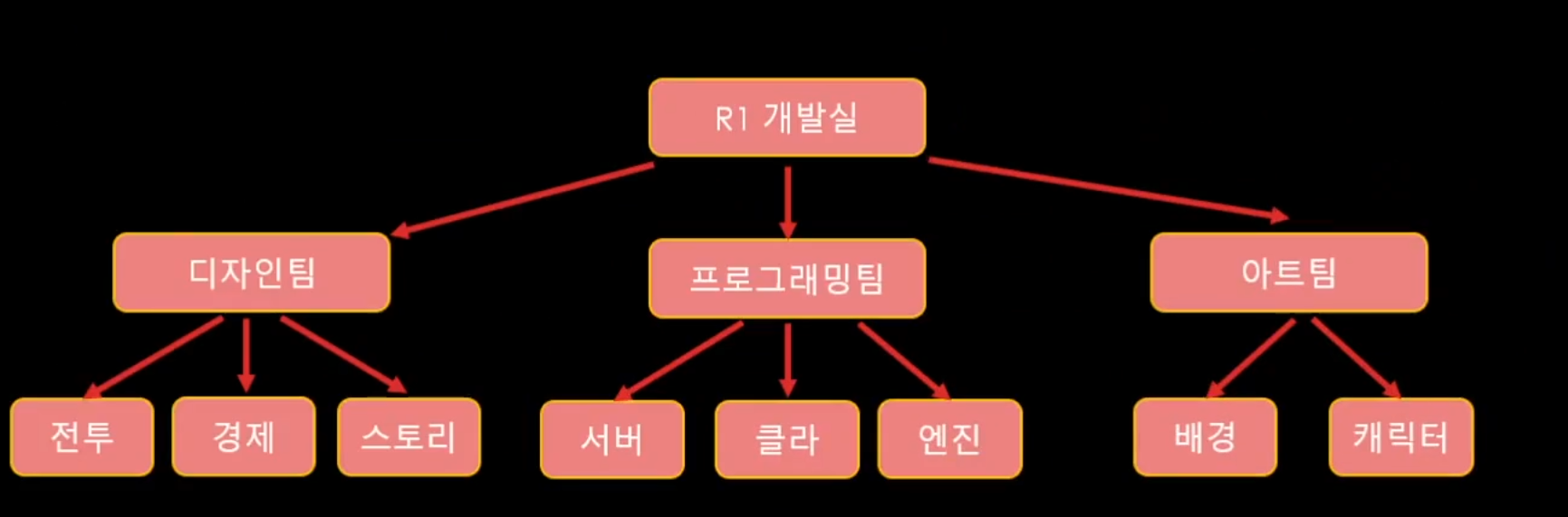
트리의 예시로는 이런것이 있다.

이것을 왜 List로 구현을 못하였냐 하면 List는 앞뒤로 하나씩만 가질 수 있지만
이것같은 경우에는 하나가 여러개를 가지고 있기때문에 구현을 할 수가 없다.

트리는 개념은 단순하지만 응용이 어렵다.

트리 관련 용어로는 이러한 것들이 있다.

• 부모(parent) 노드
  • 말 그대로 노드의 부모가 되는 노드
• 자식(child) 노드
  • 말 그대로 노드의 자식이 되는 노드
• 형제(sibling) 노드
  • 말 그대로 동일선상의 노드
• 선조(ancestor) 노드
  • 말 그대로 자식의 부모의 부모
• 자손(descendant)
  • 말 그대로 부모의 자식의 자식
• 루트(root)
  • 최상위 노드
• 잎(leaf)
  • 최하위 노드
• 깊이(depth)
  • 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
• 높이(height)
  • 루트 노드에서 가장 깊숙히 있는 노드의 깊이
• 트리의 재귀적 속성 및 서브트리(subtree)

트리를 이해할 때 가장 중요하게 이해해야 하는 것은
왜 재귀함수를 사용하면 궁합이 잘 맞는지에 대해 알아야 한다.

트리를 나무라고 보면 나무의 가지를 잘라도 그것대로 트리라고 볼 수 있다.
즉 어떠한 코드를 만들 때 재귀함수를 이용하면 트리 구조를 훨씬 쉽게 구현하거나 탐색할 수 있다.

음 그럼 트리로는 무엇을 만들 수 있을까?
솔직히 우리가 일상에서 많이 사용할 일은 없다.
만들어도 특성트리?정도 라고 볼 수 있지만
이 트리가 기본기가 되어서 고급 기법을 만드는 데에 도움이 되고
우선순위 큐, 레드 블랙 트리 등을 구현 할 때도 사용된다.

구현

만약에 우리가 트리를 구현하게 된다면 앞서 배운 Vector를 사용하여 만들 수 있을 것이다.
우리가 트리에게 이어진 노드에 개수를 모르기 때문에 동적으로 늘어나는 배열인 Vector를 사용하여 node들을 만들어주면 될 것 이다.
그리고 children이라는 변수를 만들어서 부모에서 그 노드들을 이어주면 될 것이다.

#include <iostream>
using namespace std;
#include <vector>

class Node
{
public:
	Node(const char* data) : data(data) { }

public:
	const char* data;
	vector<Node*> children;
};

Node* CreateTree()
{
	Node* root = new Node("R1 개발실");
	{
		Node* node = new Node("디자인");
		root->children.push_back(node);
		{
			Node* leaf = new Node("전투");
			node->children.push_back(leaf);
		}
		{
			Node* leaf = new Node("경제");
			node->children.push_back(leaf);
		}
		{
			Node* leaf = new Node("스토리");
			node->children.push_back(leaf);
		}
	}
	{
		Node* node = new Node("프로그래밍");
		root->children.push_back(node);
		{
			Node* leaf = new Node("클라");
			node->children.push_back(leaf);
		}
		{
			Node* leaf = new Node("서버");
			node->children.push_back(leaf);
		}
		{
			Node* leaf = new Node("엔진");
			node->children.push_back(leaf);
		}
	}
	{
		Node* node = new Node("아트");
		root->children.push_back(node);
		{
			Node* leaf = new Node("배경");
			node->children.push_back(leaf);
		}
		{
			Node* leaf = new Node("캐릭터");
			node->children.push_back(leaf);
		}
	}

	return root;
}

그럼 어떤식으로 출력해볼 수 있을까?

일단 생각 해보면 root의 size를 받아서 for문을 돌려준다.
라고 생각하면 안된다.
왜냐하면 그 안에 얼마난 노드들이 파고 들지 모르기 떄문이다.

이럴 때 재귀함수를 사용한다.

void PrintTree(Node* root)
{
	cout << root->data << endl;

	int size = root->children.size();
	for (int i = 0; i < size; i++)
	{
		Node* node = root->children[i];
		PrintTree(node);
	}
}

이런식으로 출력해볼 수 있다.

하지만 이런식으로 출력한다면 보기 불편할 것이다.
그래서 우리는 깊이 구해서 계층구조를 나타내 줄 것이다.

깊이는 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 개수이다.

void PrintTree(Node* root, int depth = 0)
{
	for (int i = 0; i < depth; i++)
		cout << "-";

	cout << root->data << endl;

	int size = root->children.size();
	for (int i = 0; i < size; i++)
	{
		Node* node = root->children[i];
		PrintTree(node, depth + 1);
	}
}

이러면 대충 트리를 어떤식으로 만들고 출력하는지 알 수 있게 된다.

그리고 트리의 높이를 구현해보기 위한 코드도 구현 해볼 것이다.
왜냐하면 이러한 문제 유형이 있다고 해서이다.

높이의 경우 깊이보다 생각할 것들이 많아진다.

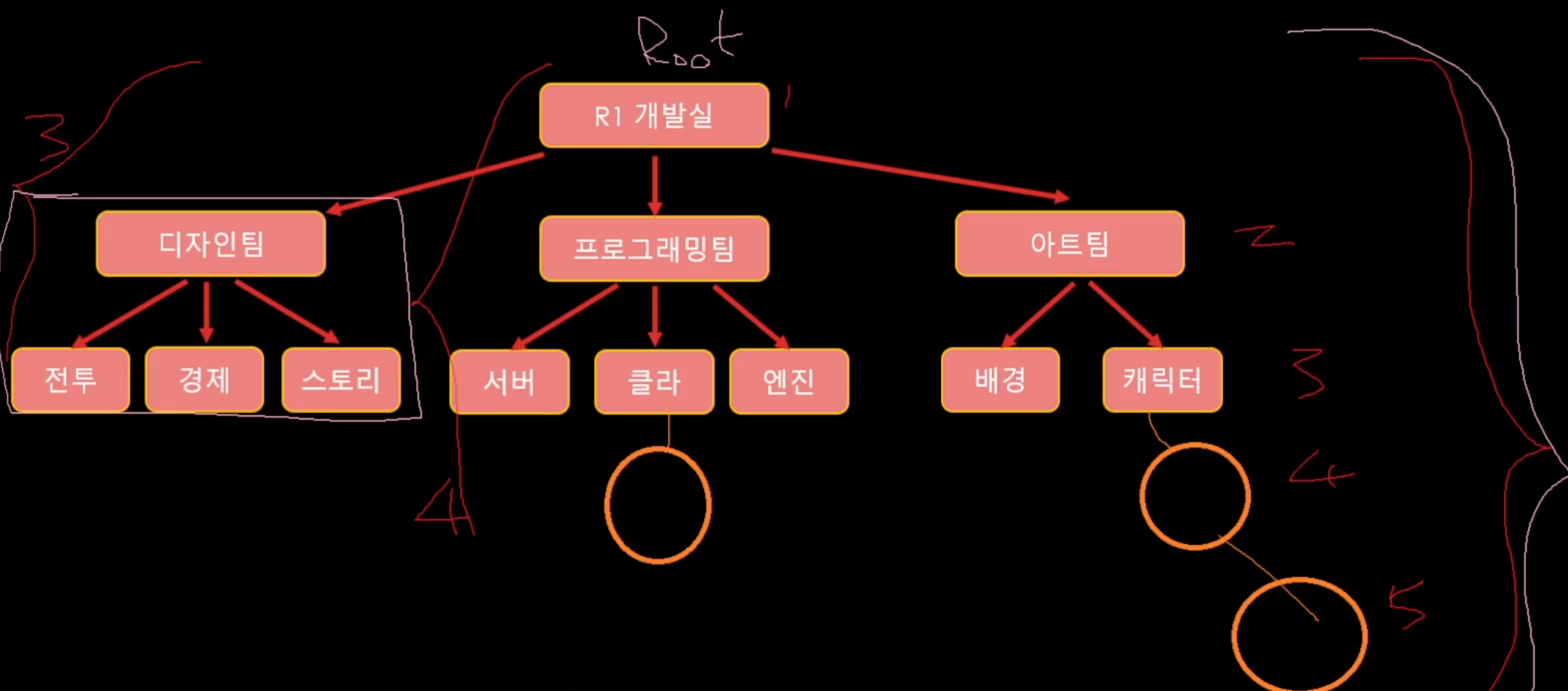
이것처럼 높이는 루트의 맨 아래의 노드를 기준으로 깊이를 구해야 하는 것이기 때문에 루트의 자식노드 중에서 가장 높이 높은 노드의 높이 + 1을 해줘야 한다.

// 높이
int GetHeight(Node* root)
{
	int ret = 1;

	int size = root->children.size();
	for (int i = 0; i < size; i++)
	{
		Node* node = root->children[i];
		int h = GetHeight(node) + 1;
		
		if (ret < h)
			ret = h;
	}

	return ret;
}

이런식으로 구현해 줄 수 있다.
노드가 하나일 때 1이니 기본값을 1로 초기화하고
루트 노드의 자식 노드의 개수만큼 for문을 돌려 node를 생성해주고
GetHeight() 재귀함수를 돌려서 최종 높이를 구하고
그 높이가 결과값 보다 크면 덮어씌우는 방식으로 만들어줄 수 있다.

정리

트리는 계층적 구조를 갖는 데이터를 표현하기 위한 자료구조이다.
트리는 레드 블랙 트리처럼 서칭할 때 가장 많이 사용된다.

트리는 너무 코어(기초)이기 때문에 직접 만들어서 사용할 일은 별로 없지만 다른 부분과 응용하여 많이 사용되는 자료구조이다.

나중에 한 번더 복습하자