강의 보고 공부한 것을 정리하는 목적으로 작성된 글이므로 틀린 점이 있을 수 있음에 양해 부탁드립니다. (피드백 환영입니다)

저번에 말하였던 이진 탐색의 한계때문에 이진 탐색 트리를 공부해볼 것이다.

이진 탐색 트리

이진 탐색 트리(Binary Search Tree)는 이진 트리와 같이 최대 두 개의 자식을 가질 수 있고 왼쪽은 무조건 작은 값 오른쪽은 무조건 큰 값으로 분류되는 트리이다.

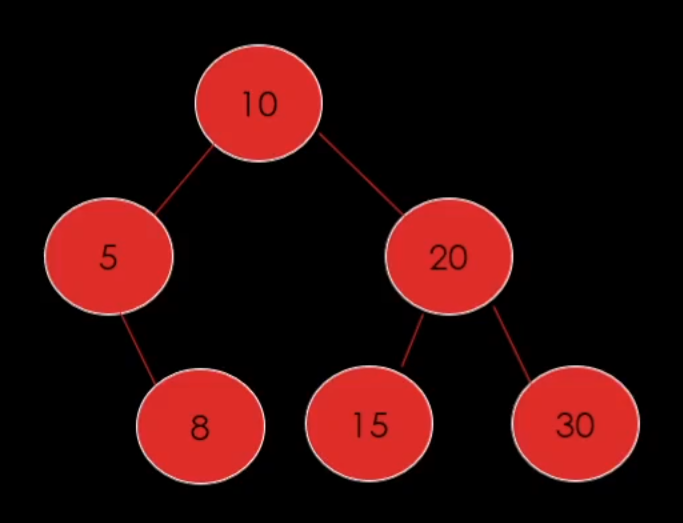
옳은 버전

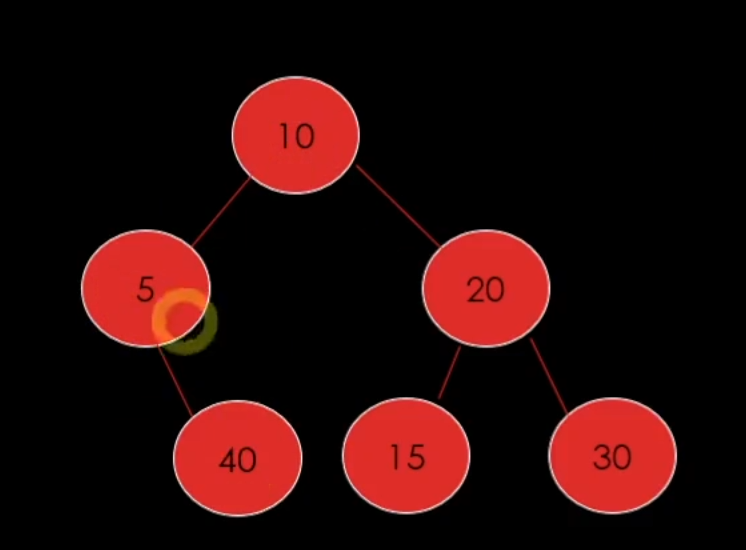
틀린 버전
40은 5보다는 크기만 10보다는 안 작다.

이런 규칙대로 분류를 시킨다.

데이터를 추가 시키는 경우

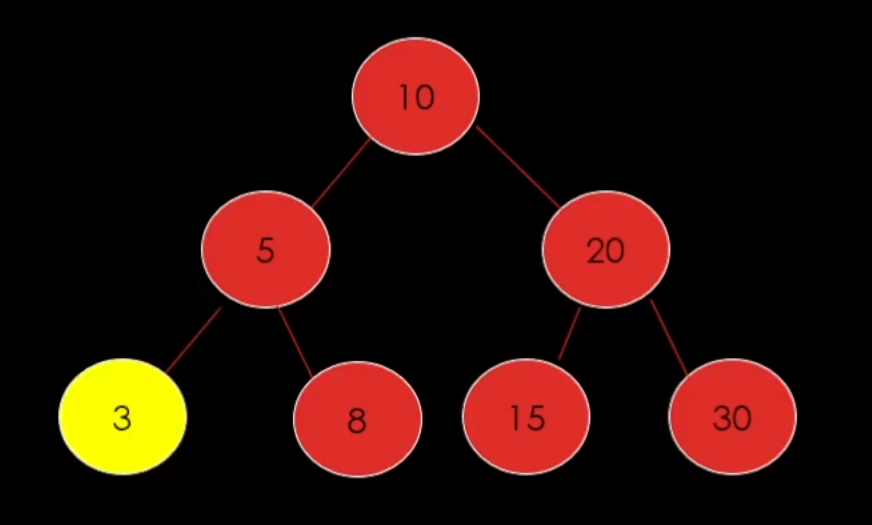
우리가 3이라는 값을 추가시킨다면 우리는 이런식으로 판별해서 값을 넣어줄 수 있을 것이다.

3은 10보다 작다 -> 왼쪽
3은 5보다 작다 -> 왼쪽
더 이상 데이터가 없다 -> 3삽입

데이터를 삭제 시키는 경우

데이터를 추가 시키는 경우보다는 복잡하다.

첫 번째로 삭제할 노드가 자식이 아예 없는 경우이다.

우리가 8을 삭제 해야 된다! 라고 한다면 별로 규칙에 위배되는 것이 없기때문에 그냥 삭제를 해줄 수 있다.

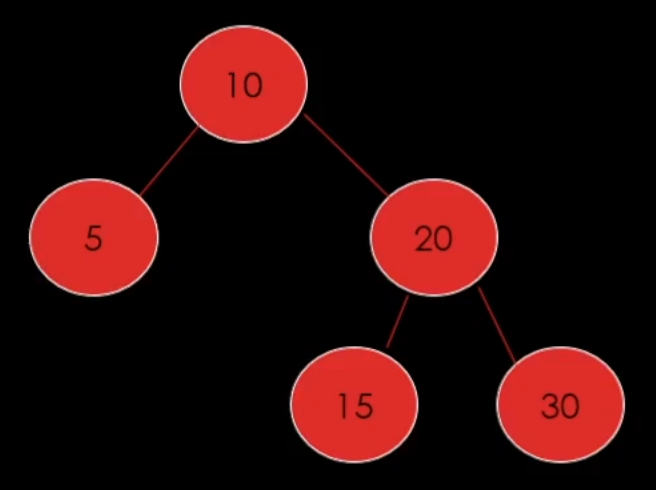
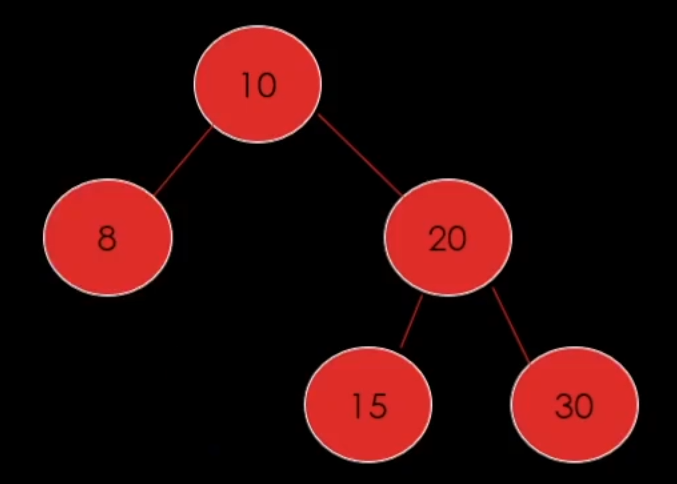
두 번째로 삭제할 노드에 자식이 1개가 있는 경우이다.

우리가 5를 삭제 해야 된다! 라고 한다면 5를 삭제하면 끊어지기 때문에 연결을 해줘야 한다. 그래서 5가 있는 자리에 8을 옮겨주면 된다.

세 번째로 삭제할 노드가 자식이 2개인 경우이다.

우리가 10을 삭제 해야 된다! 라고 한다면 10을 삭제하면 자식을 올려야 하는데 무슨 자식을 올려야하는지 애매해진다.

이럴 때에는 10 다음으로 큰 값을 찾아준다(15). 그러면 15를 10에 자리로 옮겨준다. 그리고 원래 자리에 있던 15를 삭제해준다.

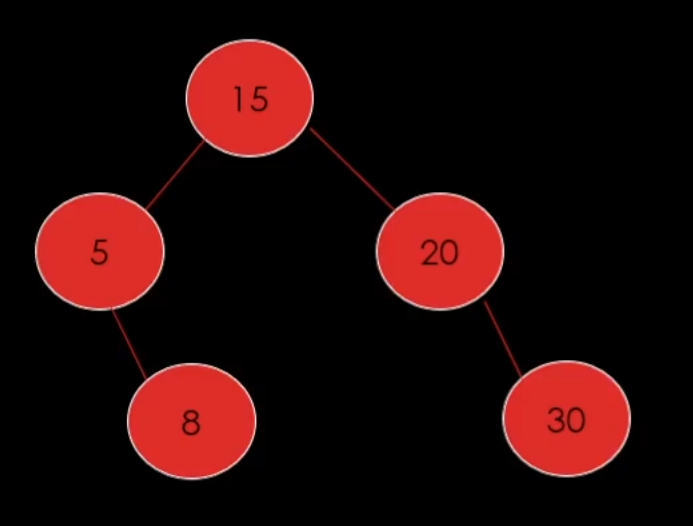
그래서 우리는 이진 탐색 트리를 공부할 때 모든 노드가 자식을 최대 2개까지 가질 수 있고 왼쪽은 무조건 작은 값이 들어가고 오른쪽은 무조건 큰 값이 들어간다는 규칙만 기억하고 있으면 된다.

그래서 우리는 이것을 구현해볼 것이다.

이진 탐색 트리 구현

일단 노드라는 개념이 필요하기 때문에 Node를 구현해줄 것이다.

struct Node
{
	Node* parent = nullptr;
	Node* left = nullptr;
	Node* right = nullptr;
	int key = 0;
};

그리고 이진 탐색 트리의 토대를 만들어 줄 것이다.

class BinarySearchTree
{
public:

private:
	Node* _root = nullptr;
};

이런식으로 간단하게 root노드만 가지고 있게 만들어준다.

우리는 먼저 insert함수를 만들어줄 것이다.

void BinarySearchTree::Insert(int key)
{
	// 새로운 노드 생성
	Node* newNode = new Node();
	// key값 넣어주기
	newNode->key = key;

	// root가 없으면
	if (_root = nullptr)
	{
		_root = newNode;
		return;
	}

	// 추가할 위치를 찾기
	// 위치 추적을 위한 node
	Node* node = _root;
	// 부모님이 누군지
	Node* parent = nullptr;

	// null을 만날 때 까지
	while (node)
	{
		parent = node;
		// left
		if (key < node->key)
			node = node->left;
		// right
		else
			node = node->right;
	}

	newNode->parent = parent;

	// 어디서 추가가 되었는가?
	if (key < parent->key)
		parent->left = newNode;
	else
		parent->right = newNode;
}

그리고 이것은 시각적으로 보기 위해서 Print함수를 만들어 줄 것이다.
이것도 출력하는 방식이 다양하지만 우리는 부모를 먼저 출력하고 왼쪽 오른쪽 순서대로 출력을 해볼 것이다.

#include <iostream>
#include <Windows.h>
using namespace std;

// 지정하고 싶은 위치에 출력하기 위함
void SetCursorPosition(int x, int y)
{
	HANDLE output = ::GetStdHandle(STD_OUTPUT_HANDLE);
	COORD pos = { static_cast<SHORT>(x), static_cast<SHORT>(y) };
	::SetConsoleCursorPosition(output, pos);
}

void BinarySearchTree::Print(Node* node, int x, int y)
{
	// 예외 처리 null이면 return
	if (node == nullptr)
		return;

	// 커서 조정
	SetCursorPosition(x, y);

	cout << node->key;

	// 뒤에 공식은 예쁘게 출력하기 위함임
	Print(node->left, x - (5 / (y + 1)), y + 1);
	Print(node->right, x + (5 / (y + 1)), y + 1);
}

이런식으로 코드를 짜준다.
그리고 출력을 해본다면

#include "BinarySearchTree.h"

int main()
{
	BinarySearchTree bst;

	bst.Insert(20);
	bst.Insert(30);
	bst.Insert(10);

	bst.Print();
}

이렇게 출력이 되는 것을 알 수 있다.

그 다음으로는 Search함수를 만들어 줄 것이다.

Node* BinarySearchTree::Search(Node* node, int key)
{
	// 못찾으면 nullptr 리턴, 찾으면 찾은 node 리턴
	if (node == nullptr || key == node->key)
		return node;

	// key가 node의 key보다 작으면 왼쪽으로
	if (key < node->key)
		return Search(node->left, key);
	// 아니면 오른쪽으로!
	else
		return Search(node->right, key);
}

이런식으로 구현해주면 된다.

그리고 이제 대망의 삭제하는 부분을 만들었어야 하는데 이론으로도 삭제하는 부분은 좀 번거로운 부분이 있었다.
그래서 헬퍼함수인 Min과 Max와 Next 먼저 만들어 볼 것이다.
여기서 Min과 Max는 만들기 간단하짐나 Next는 조금 힘들 수 있다.

Node* BinarySearchTree::Min(Node* node)
{
	if (node == nullptr)
		return nullptr;
	while (node->left)
		node = node->left;

	return node;
}

Node* BinarySearchTree::Max(Node* node)
{
	if (node == nullptr)
		return nullptr;
	while (node->right)
		node = node->right;

	return node;
}

Node* BinarySearchTree::Next(Node* node)
{
	if (node->right)
		return Min(node->right);

	Node* parent = node->parent;

	while (parent && node == parent->right)
	{
		node = parent;
		parent = parent->parent;
	}
	return parent;
}

이런식으로 구현해줄 수 있다.

그리고 마지막으로 Replace라는 서브트리를 교체시키는 함수를 만들 것이다.
Replace는 만약에 중간에 값을 삭제해 버렸을 때 이어주는 함수이다.

void BinarySearchTree::Replace(Node* u, Node* v)
{
	// u가 root라는 뜻
	if (u->parent == nullptr)
		_root = v;
	// u가 부모의 왼쪽 노드일 때
	else if (u == u->parent->left)
		u->parent->left = v;
	// u가 부모의 오른쪽 노드일 때
	else
		u->parent->right = v;

	// 경우따라 nullptr로 넣을 수 있기에 예외처리
	if (v)
		v->parent = u->parent;

	delete u;
}

replace는 대충 이런식으로 돌아가는 함수이다.

그러면 이제 최종적으로 delete를 만들어주면 된다.

void BinarySearchTree::Delete(int key)
{
	Node* deleteNode = Search(_root, key);
	Delete(deleteNode);
}

void BinarySearchTree::Delete(Node* node)
{
	// nullptr 체크
	if (node == nullptr)
		return ;

	// 자식 여부에 따라 처리
	
	// 왼쪽 자식이 없을 때
	if (node->left == nullptr)
	{
		Replace(node, node->right);
	}
	// 오른쪽 자식이 없을 때
	else if (node->right == nullptr)
	{
		Replace(node, node->left);
	}
	// 양쪽에 자식이 다 있을 때
	else
	{
		// root 다음으로 큰 수 찾기
		Node* next = Next(node);
		node->key = next->key;
		Delete(next);
	}
}

이런식으로 위에 규칙과 동일하게 구현을 해주면 된다.

자 그러면 한 번 만든 것들을 사용해 본다면

int main()
{
	BinarySearchTree bst;

	bst.Insert(20);
	bst.Insert(30);
	bst.Insert(10);

	bst.Insert(25);
	bst.Insert(26);
	bst.Insert(40);
	bst.Insert(50);

	bst.Print();
}

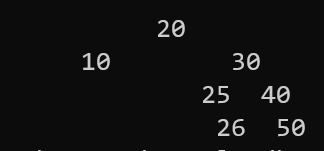
이런식으로 출력이 되고

Delete를 써본다면

int main()
{
	BinarySearchTree bst;

	bst.Insert(20);
	bst.Insert(30);
	bst.Insert(10);

	bst.Insert(25);
	bst.Insert(26);
	bst.Insert(40);
	bst.Insert(50);

	bst.Delete(26);

	bst.Print();
}

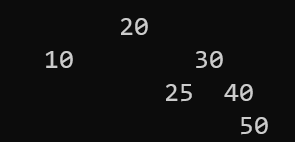
이런식으로 잘 지워지는 것을 알 수 있다.

우리는 이 세부적인 코드를 전부 이해하는 것이 아니라
이진 탐색 트리가 무엇인가?에 대한 핵심 내용만 알고 있으면 된다.

이진 탐색이 vector기반이여서 중간 삽입/삭제가 어려움
-> 중간 삽입/삭제가 용이한 트리로 만들어 버림

음 그러면 이진 탐색 트리으로 만족하면 될까?

이진 탐색 -> O(logN) -> 데이터 추가/삭제 어려움..
이진 탐색 트리 -> O(logN) -> 무언가 부족함

이진 탐색 트리가 부족한 것은 균형이다..
균형이 잘 맞으면 O(logN)이지만..

이런식으로 한쪽으로 값을 쭉 넣어서 쏠리게 된다면 솔직히 연결 리스트랑 다를께 없게 되어서 O(N)이 되어 버린다.

그래서 우리는 이것을 개선하기 위해서 균형을 맞춰줘서 한 쪽으로 쏠리지 않게만 만들어주면 되는데 그것이 Red-Black-Tree이고 그것을 구현한 표준 방식이 map이다.

그래서 다음시간에는 Red-Black-Tree을 배울 것이다!

마무리

일단 다음에 Red-Black-Tree를 배우기 전에 왜 Red-Black-Tree까지 갔어야 하는지 기억을 해야한다.

이진 탐색은 빠르지만 데이터 추가/삭제가 어렵다.
그래서 데이터 추가/삭제가 편한 트리 구조로 이진 탐색 트리를 만들었다.
하지만 이진 탐색 트리는 균형이 맞지 않는다면 연결리스트과 다를빠가 없게 되어서 느려진다.
그래서 우리가 Red-Black-Tree를 배우는 것이다.

✅기억하자!