동적계획법을 보면 알고리즘이나 인공지능쪽에서는 비중이 높다.
솔직히 게임쪽에서는 DP를 사용할 일이 거의 없다. ( 코테 제외 )
하지만 이런걸 할 수 있다는 것은 어쨋든 자신의 무기가 늘어나는 것이기에 공부해볼 것이다.
Combination (이항계수) 문제

상자 안에 공 5개가 있는데 공 2개를 뽑는 경우의 수는?
확율과 통게같은 즉 수학시간에 배웠던 것이다.
이걸 공식화해서 만들어보면
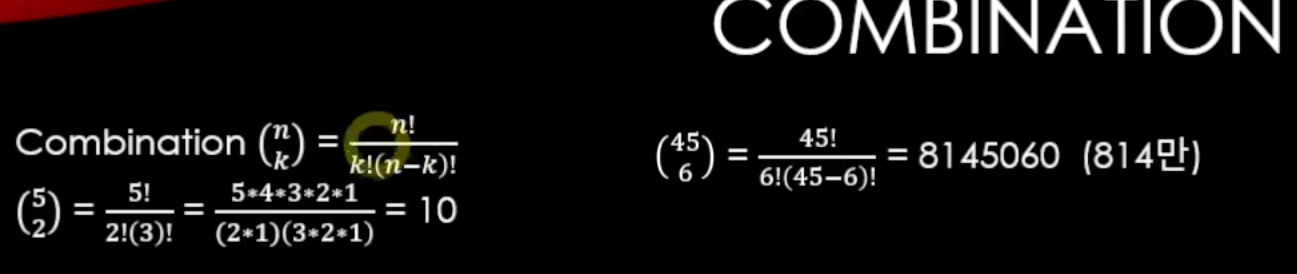
n에서 k개를 뽑는다면 위 공식을 사용해 값을 구할 수 있다.
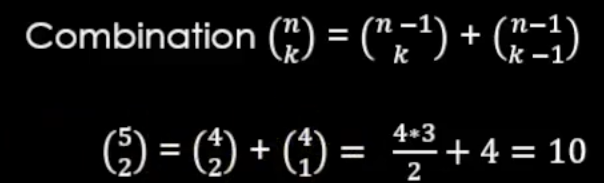
그리고 애가 특징을 가지고 있는 것이 n개에서 k개를 뽑는것은 ( n-1 / k ) + ( n - 1 / k - 1 ) 이라는 공식을 가지고 있다.
그럼 우리가 이걸 코드로 가지고 가서 구현을 해본다고 하자.
#include <windows.h>
int combination(int n, int r)
{
// 기저 사항
if ( r == 0 || n == r )
return 1;
return combination(n - 1, r - 1) + combination(n - 1, r);
}
int main()
{
__int64 start = GetTickCount64();
int letto = combination(45, 6);
__int64 end = GetTickCount64();
cout << end - start << "ms" << endl;
}이런식으로 위 공식 그대로 코드를 짤 수 있을 것이다.
하지만 여기서 아쉬운것이 있는데,
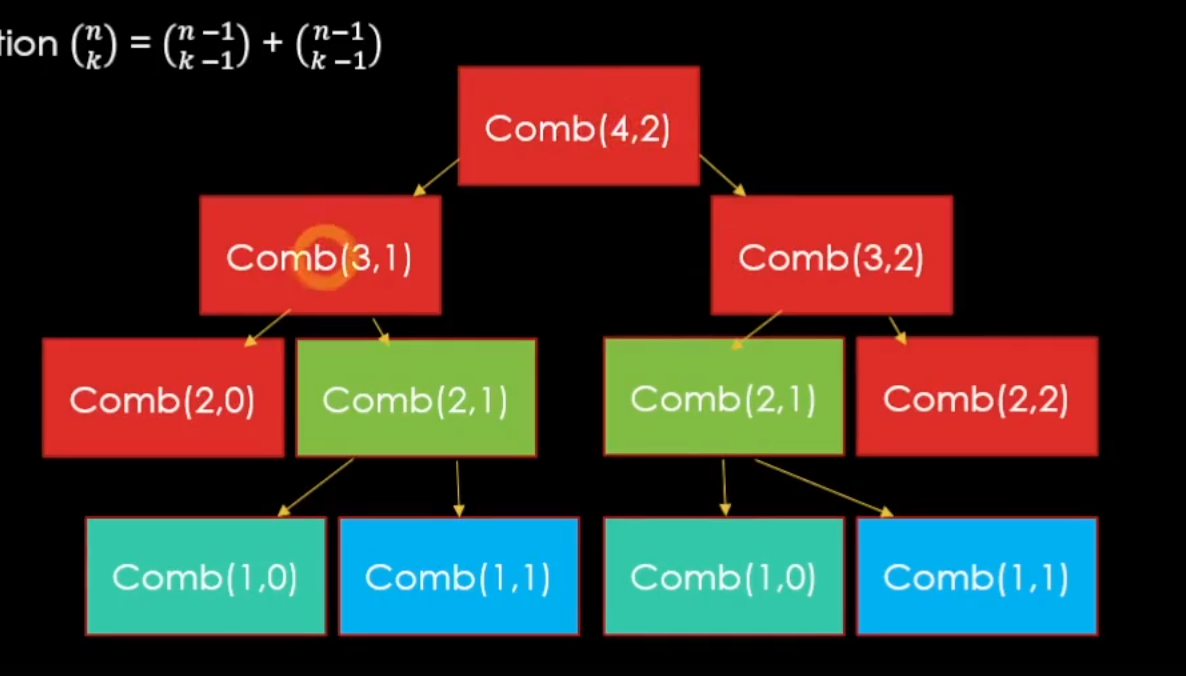
바로 중복되어 계산되는 것들이 많다는 것이다.
값이 작으면 상관이 없겠지만 45, 6처럼 값이 많아지게 된다면 중복으로 호출되는 것이 많아서 엄청난 부담이 될 것이다.
그래서 반복횟수를 줄이기 위해 어디에다가 결과를 보관했다가 사용하면은 좋아질 것이지만 지금은 무식하게 동일한 값을 반복하고 있다.
#include <windows.h>
int g_count;
int combination(int n, int r)
{
// 기저 사항
if ( r == 0 || n == r )
return 1;
if (n == 2 && r == 1)
g_count++;
return combination(n - 1, r - 1) + combination(n - 1, r);
}
int main()
{
int letto = combination(45, 6);
cout << g_count << endl;
}이렇게 계산을 해보면 n이 2이고 r이 1인 경우를 962598번이나 반복하여 계산했다는 것을 알 수 있다. 사실 우리가 한 번만 계산해서 그 값을 저장하고 있다면 1번만 연산을 하면 되는데 무식하게 계산하고 있던 것이다.
그럼 이거를 어떻게 개선할 수 있는가?
cache를 해서 결과물을 저장하고 있으면 처음은 계산하겠지만 그 다음부터는 계산해논값을 빼갈 것이기에 반복된 계산을 줄일 수 있게 된다. 이게 바로 DP ( 동적 계획법이다 )
사실 게임을 만들때에는 아무 쓸모가 없지만 알파고같은거 구현하는 원리가 이것저것 계산을 해서 계산결과를 저장해서 재사용하는 것이다. 우리가 바둑을 둘 때도 이런 알고리즘을 사용하지 않지만 여러가지의 가능성이 있을 것이다. 그럴때마다 바둑의 상태를 보고 전에 만난 상태였으면 매번 무식하게 계산하는 것이 아닌 저장된 값을 보고 판별할 수 있을 것이다.
그래서 이 개념자체가 인공지능에 관련이 있다는 것을 알 수 있다.
이것을 응용해서 코드를 바꿔본다면된다.
DP문제는 문제를 푸는 규칙을 찾은 다음에 어떻게 캐쉬를 만들 것인지를 정해야 된다.
이것을 메모이제이션( memoization )이라고 부른다.
그럼 구현을 해보자
#include <windows.h>
int cache[50][50];
int combination(int n, int r)
{
// 기저 사항
if ( r == 0 || n == r )
return 1;
// 이미 답을 구한 적 있으면 바로 반환
int& ret = cache[n][r];
if(ret != -1)
return ret;
return ret = return combination(n - 1, r - 1) + combination(n - 1, r);
}
int main()
{
// 배열을 -1로 초기화
::memset(cache, -1, sizeof(cache)); // 이중 for문 대신 사용가능
__int64 start = GetTickCount64();
int letto = combination(45, 6);
__int64 end = GetTickCount64();
cout << end - start << "ms" << endl;
}여기서 cache는 n과 r이 있기 때문에 int cache[50][50]; 이런 느낌으로 만들 수 있다.
또 여기서 cache를 초기화 할 때 memset이라는 함수를 사용해서 -1로 초기화 시킬 수 있다. ( 0이나 -1로 초기화할 때 많이 쓰임 )
또한 참조값을 사용해서 원본에다가 넣어줄 수 있다.
이제 이런식으로만 바꿔줘도 원래는 46ms였던 것이 0ms로 빨라졌다.
그래서 DP문제는 cache를 만들어서 우월하게 찾겠다! 이런 느낌이다.
PLUS
추가로 강사님이 크레프톤 코테를 볼 때 ENCHANT라는 문제를 냈다고 한다.
컨셉이 어떤 무기가 있는데 +0 집행검에서 시작을 한다.
여기서 무기 강화 주문서를 바르게 되면 +1 +2 +3중 하나가 랜덤으로 뜨게 된다.
이렇게 우여곡절 끝에 +9집행검이 되었을 때 경우의 수는? 이라는 문제 였다.
예를 들어보면 +1만 되어서 9강이 된 집행검이 있을 것이고 +3만 되어서 0강이 된 집행검도 있을 것이다 즉 다양한 경우의 수가 존재한다.
그래서 그 경우의 수를 다 찾아서 더해라가 문제였다.
풀이를 해보면
int n = 9;
int cache[100];
// [+num]부터 시작해서, [+N}까지 가는 경우의 수
int Enchant(int num)
{
// 기저 사례
if(num > N)
return 0;
if(num == N)
return 1;
// 캐시
int& ret = cache[num];
if(ref != -1)
return ret;
// 적용
return ret = Enchant(num + 1) + Enchant(num + 2) + Enchant(num + 3);
}
int main()
{
memset(chche, -1, sizeof(cache));
int ret = Enchant(0);
cout << ret << endl;
}이런식으로 구현을 할 수 있는데
보면 앞에 문제와 공식은 달라졌다는 것을 알 수 있지만, 공식을 구했다 싶으면 캐시를 적용시켜서 반복적으로 구한 것을 재사용하는 것까지는 다를바가 없다.
그래서 처음에 틀을 짤 때
// 기저사항
// 캐시
// 적용이런식으로 틀을 짜면 편하다.
마무리
여기까지가 DP에 관한 내용이였다.
DP는 보기보다 별게 없는 것 같다.
DP는 아마 코테를 칠 때 필요할 것이기 때문에 DP문제를 풀다가 모르겠으면 복습을 한 번 하자