강의 보고 공부한 것을 정리하는 목적으로 작성된 글이므로 틀린 점이 있을 수 있음에 양해 부탁드립니다. (피드백 환영입니다)

전에 공부하였던 이진 탐색 트리의 완전형인 레드 블랙 트리를 공부해볼 것이다.

레드 블랙 트리

일단 레드 블랙 트리도 이진 탐색 트리에서 시작을 한 것이라고 볼 수 있다.

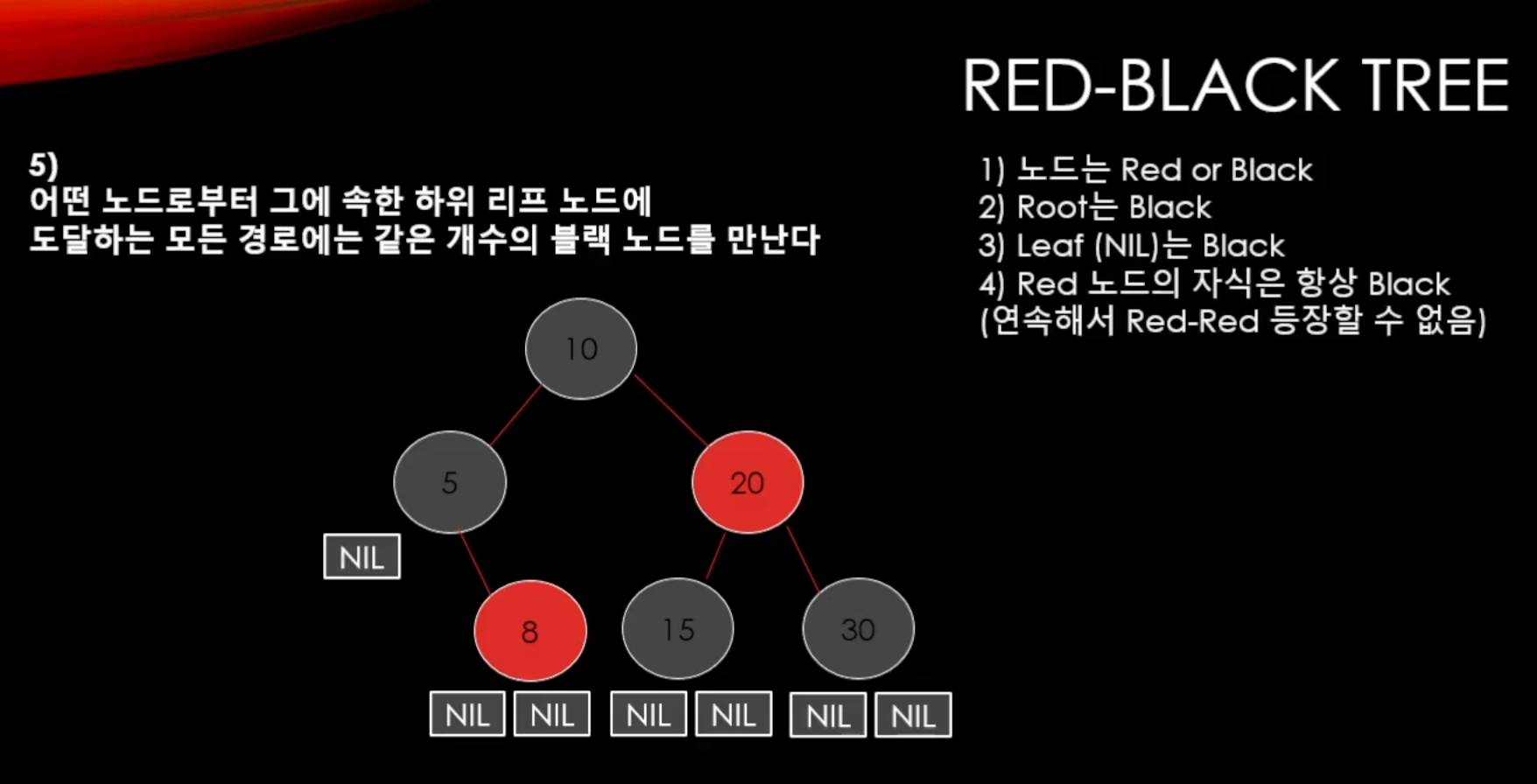
일단 레드 블랙 트리로 가면서 규칙이 추가 되게 된다.

1. 노드에다가 Red와 Black이라는 색상을 둘 것이다. (두가지의 타입)
2. Root노드는 항상 Black이다.
3. Leaf(NIL)은 항상 Black이다. (nullptr이라고 생각하면 된다)
4. Red노드의 자식은 항상 Black이다. (연속해서 Red가 나올 수 없다)
5. ✨어떤 노드로부터 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 같은 개수의 블랙 노드를 만난다.✨

5번의 추가 설명을 해보자면
만약 8번에서 시작을 한다치면
왼쪽으로 가면 블랙 노드가 2개 오른쪽으로 가도 블랙 노드가 2개로 똑같다.

5번에서 시작한다고 하면
왼쪽으로 가면 자신까지 포함해서 2개
오른쪽으로 가면 두 갈래로 나뉘는데 여기서 왼쪽 오른쪽 둘 다 동일하게 2개이다.

이런식으로 다 동일한 것이다. (이 규칙을 맞추기 위해서 난리를 부려야한다)

레드 블랙 트리로 가면 삽입/삭제 둘 다 좀 어려워진다.

RED BLACK TREE 추가

일단 추가 되는 모든 노드는 RED노드 이다.

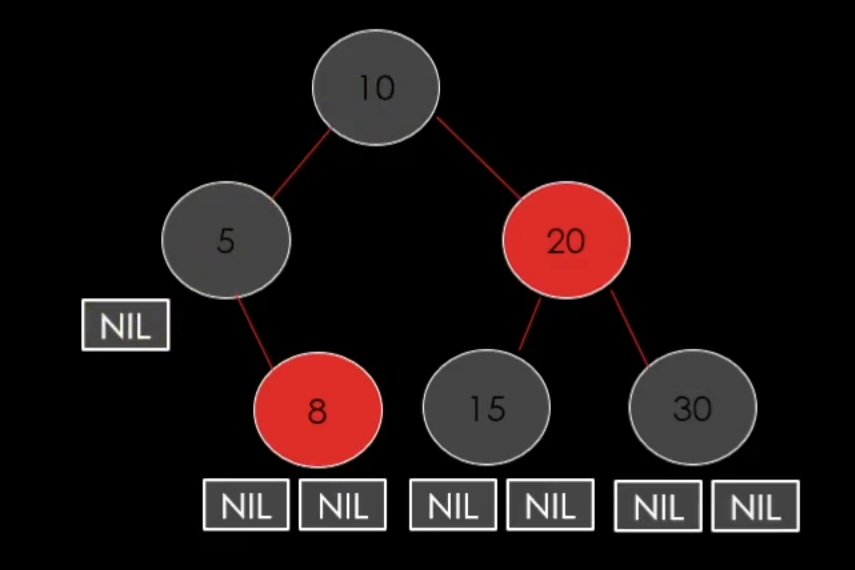
일단 여기서 4을 추가하게 된다면

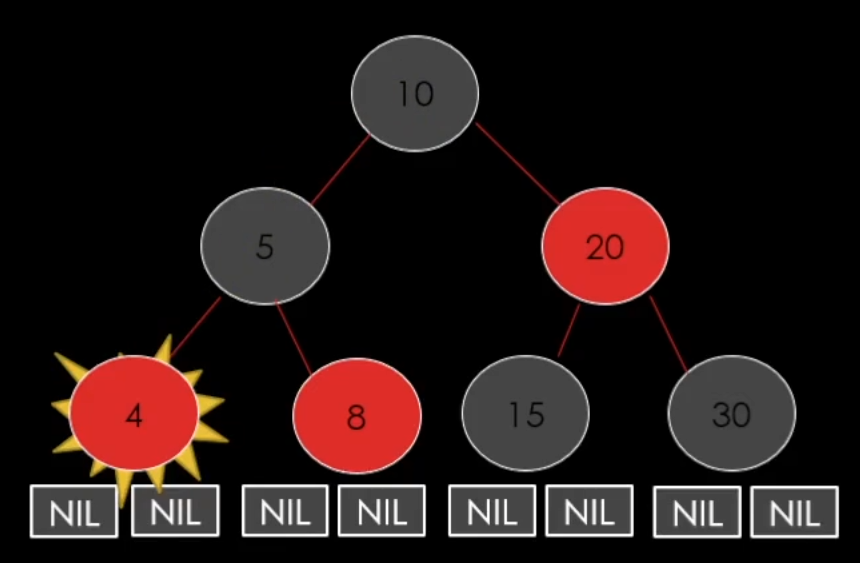
이렇게 끝이 난다.
마침 부모가 Black이기 때문에 문제가 될 것이 없다. (가장 좋은 케이스)

그럼 여기서 7을 추가한다면 어떻게 될까?

BST에 규칙대로 가보면 8노드의 왼쪽이 될 것인데..

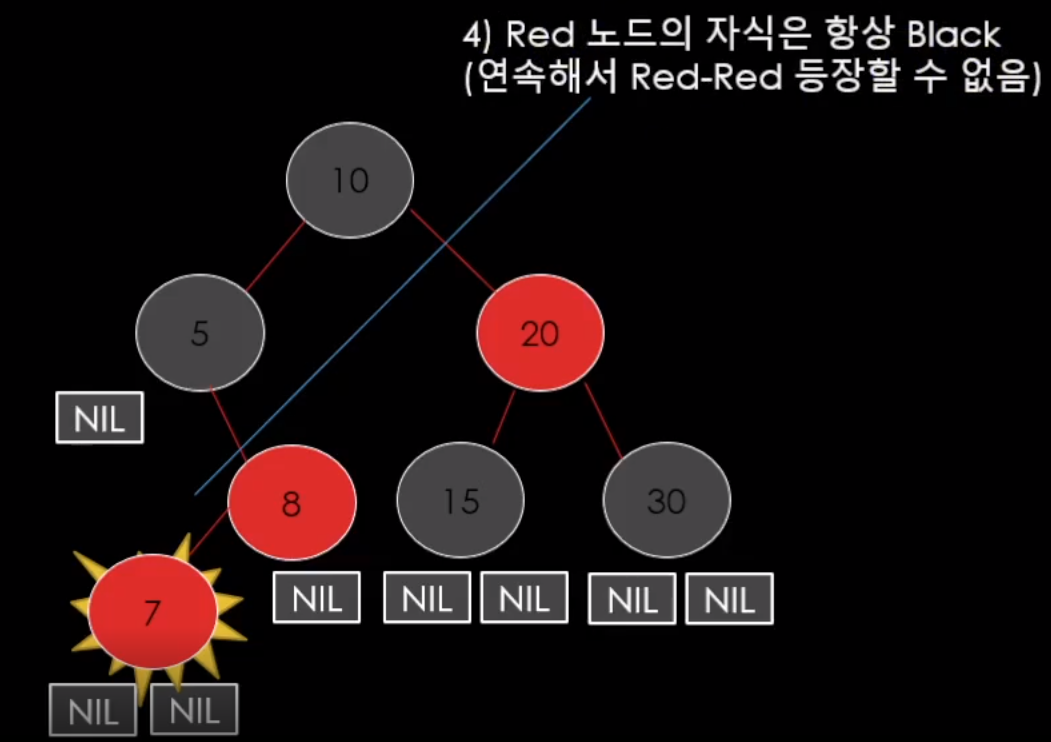
이런식으로 Red-Red가 되어서 규칙을 위배하게 된다.

여기서 구조를 바꿔줘야하는데 쉽지 않다.

그래서 이러한 공식이 있다.

P가 부모고 U이 삼촌이다.

1번째 경우는

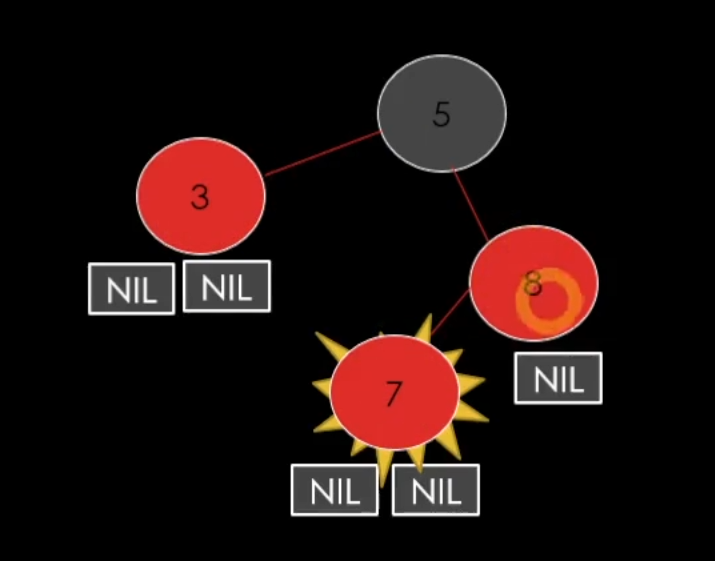
이러한 상황이다.

이러한 상황일 때 p = black, u = black, pp = red(pp체크)로 바꿔주는 공식이 있다.

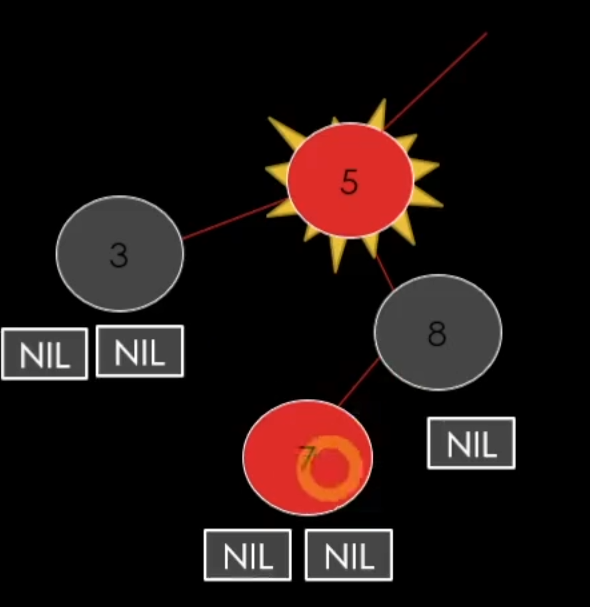
이렇게 될 것이고 5노드가 규칙 위배가 되는지 확인해야 한다.

2번째 경우는

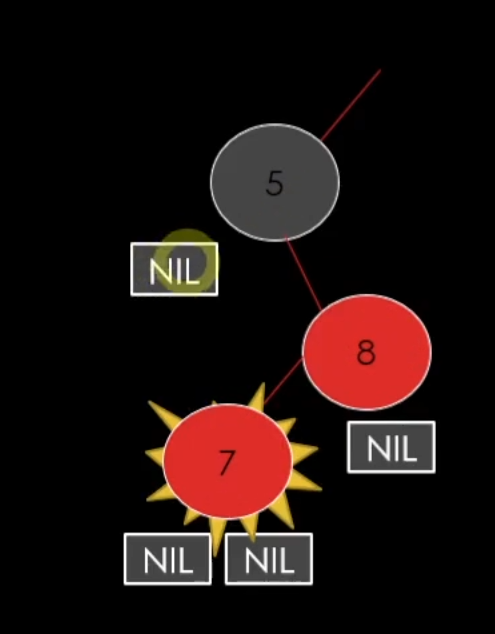
이러한 상황이다.

이러한 상황일 때에는 Rotate, 즉 돌려버려서 3번깨 경우로 만들어 버린다.

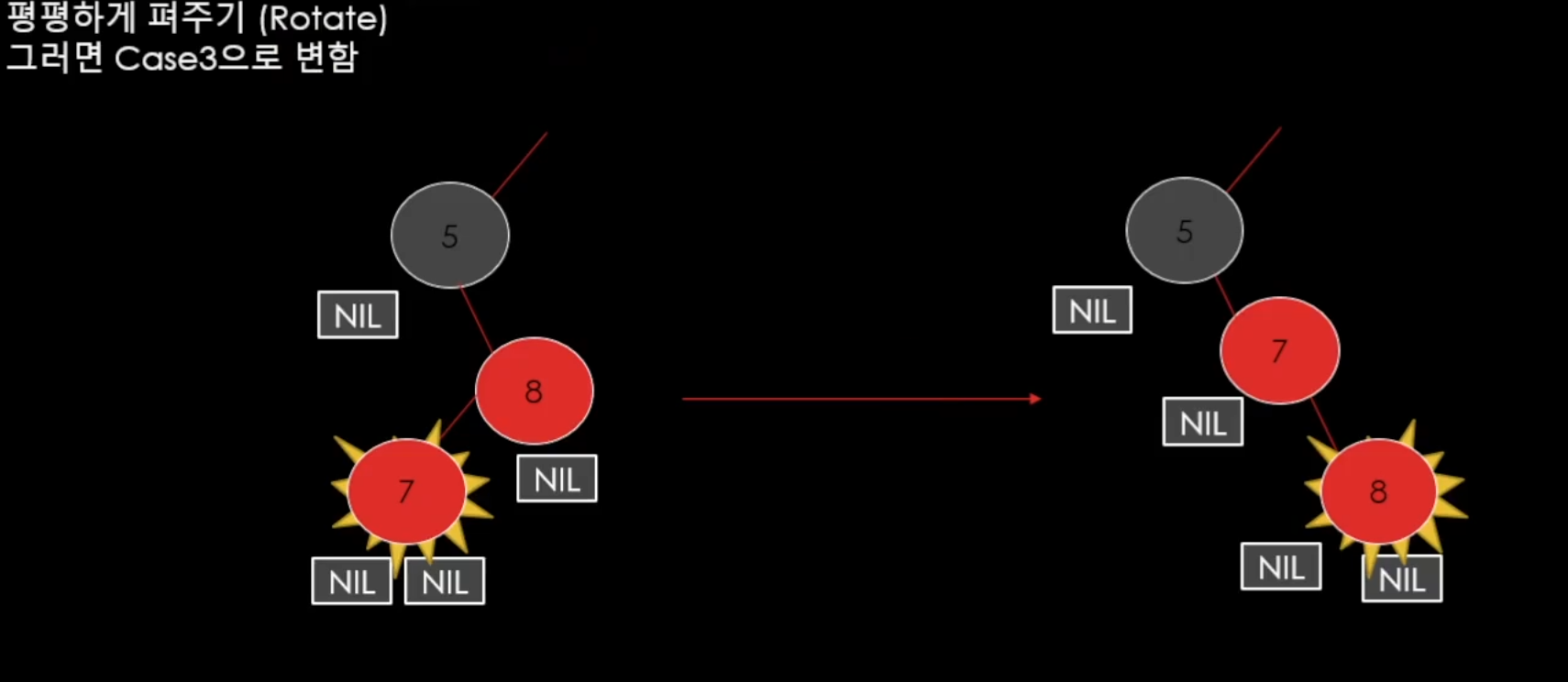
3번째 경우는

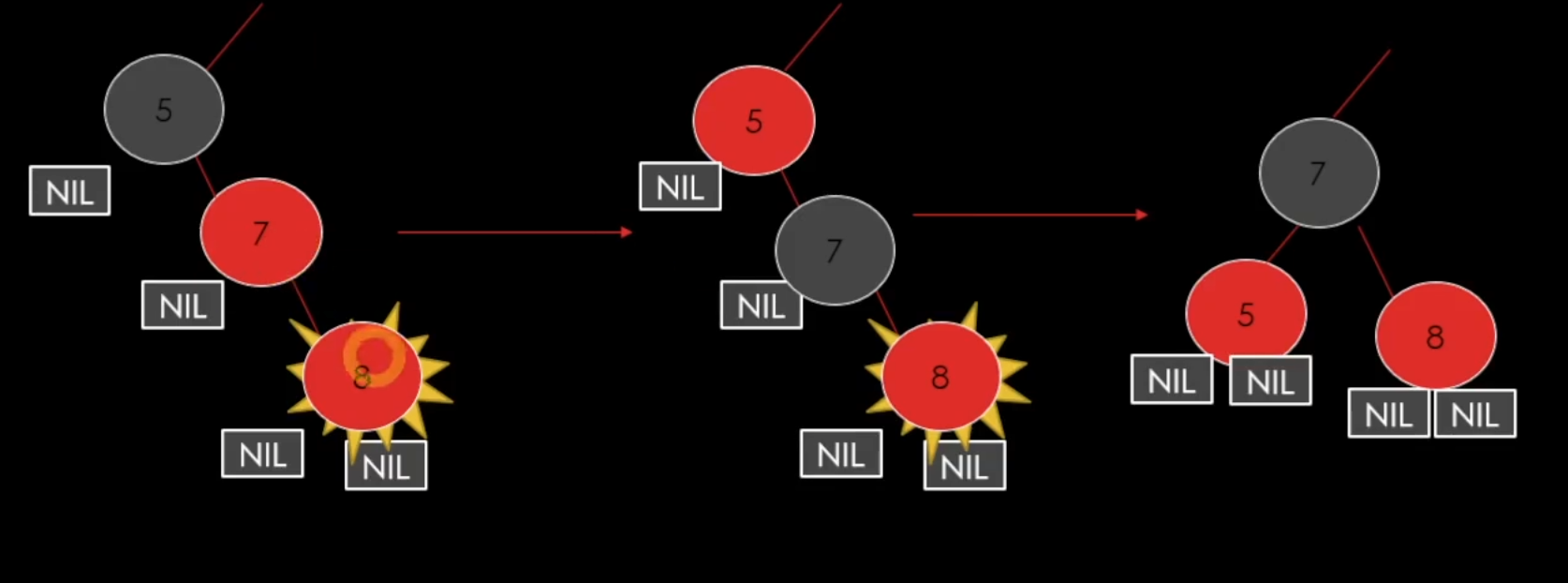
이러한 상황일 때인데

이러한 상황일 떄는 p = black으로 바꾸고 pp = red 그리고 rotate를 하여 맞춰주면 된다.

그래서 RED BLACK TREE를 추가할 때는

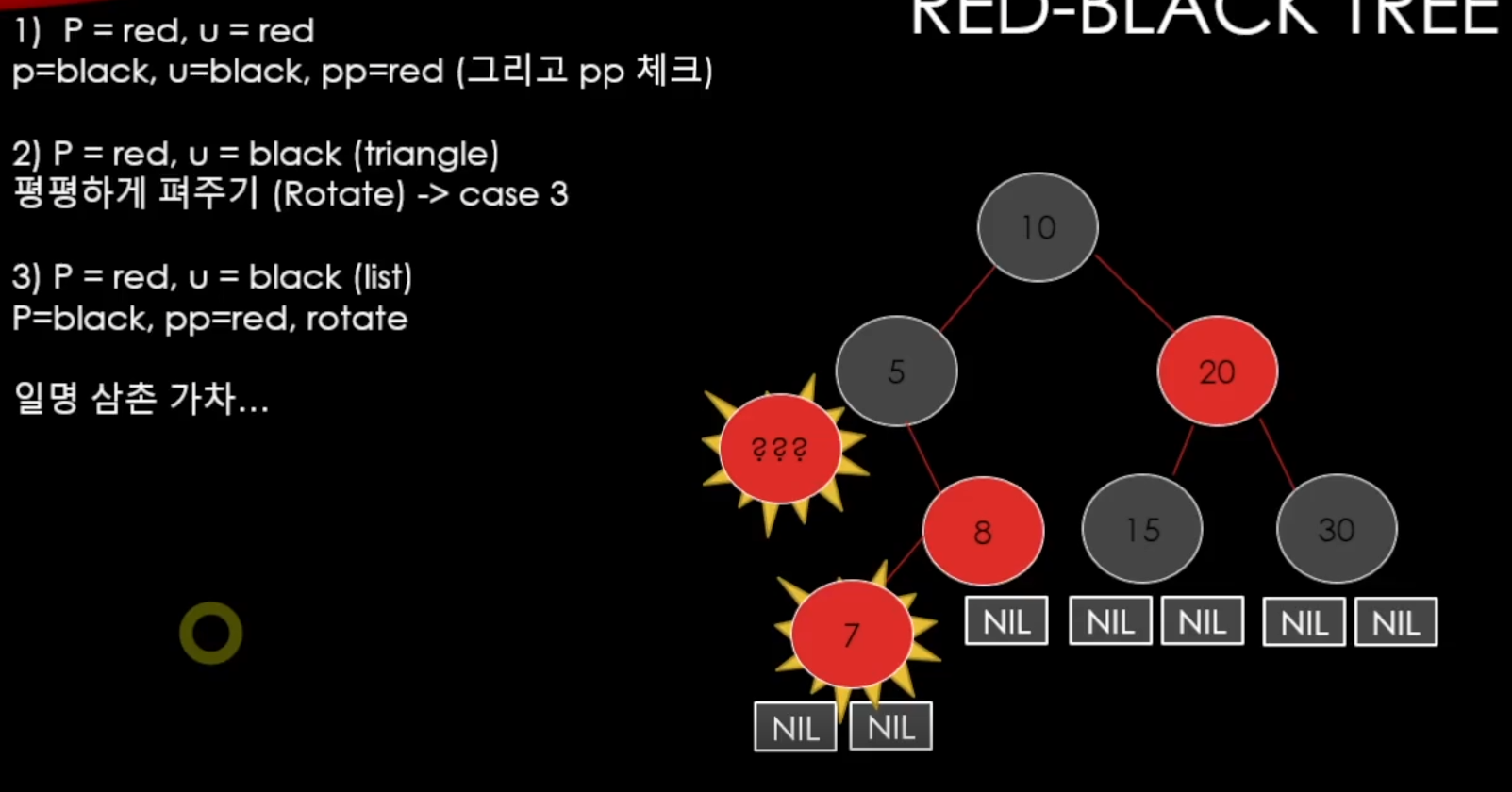
이런식이 될 것이다. (삼촌이 중요하다)

RED BLACK TREE 삭제

case 1. 삭제할 노드가 RED인 경우

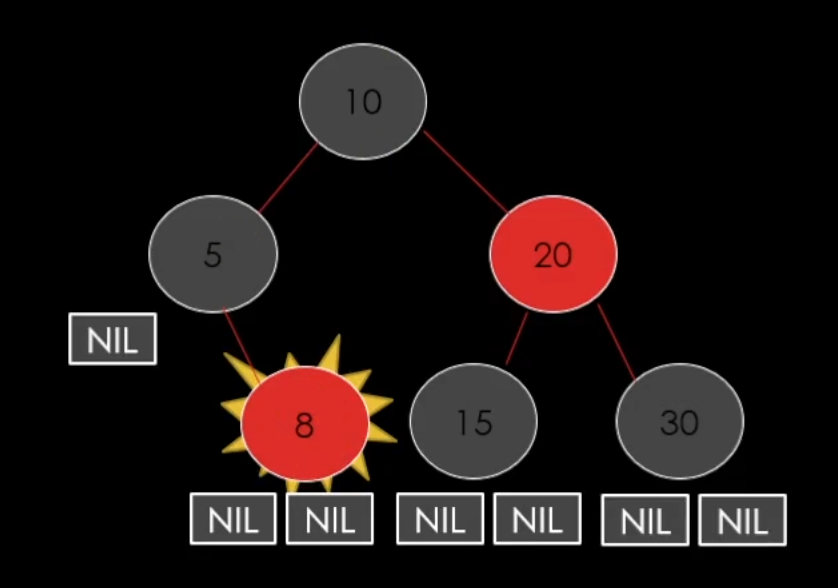
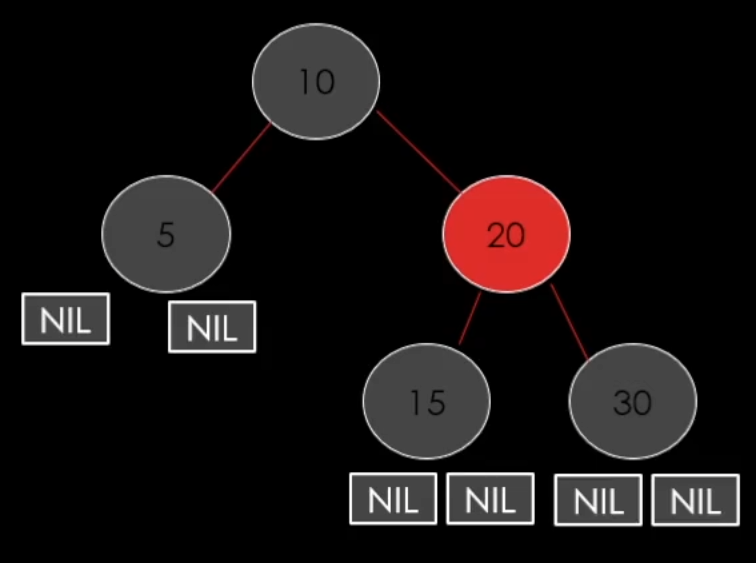
그냥 삭제 해버린면 된다. (가장 좋은 케이스)

case 2. 삭제할 노드가 Black인 경우

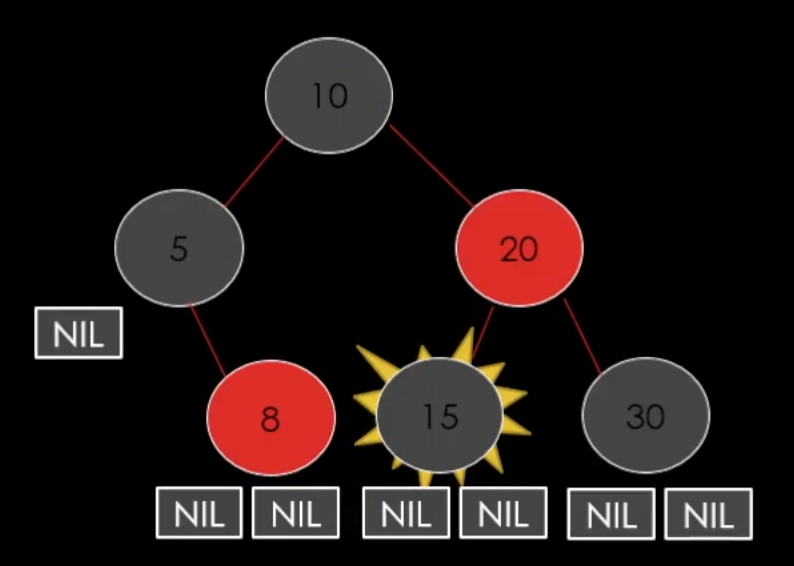
이러면 경로의 개수가 안맞게 된다.

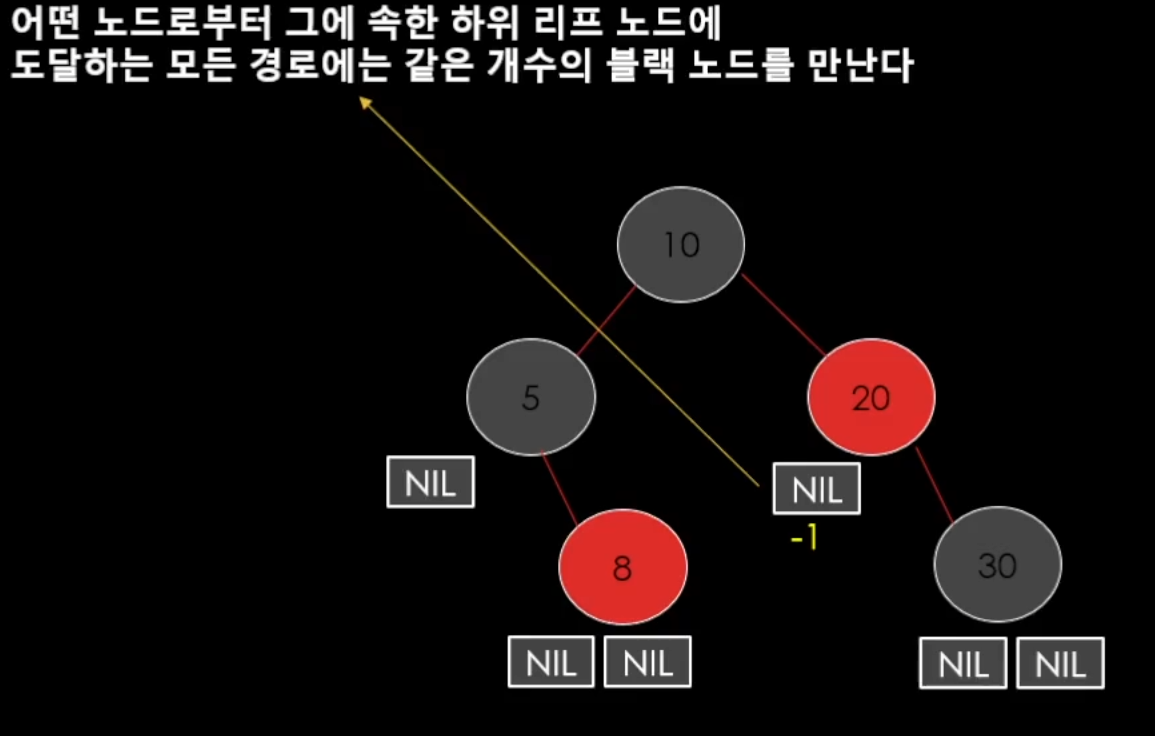
그럴 떄에는 이런식으로 처리해야 한다.

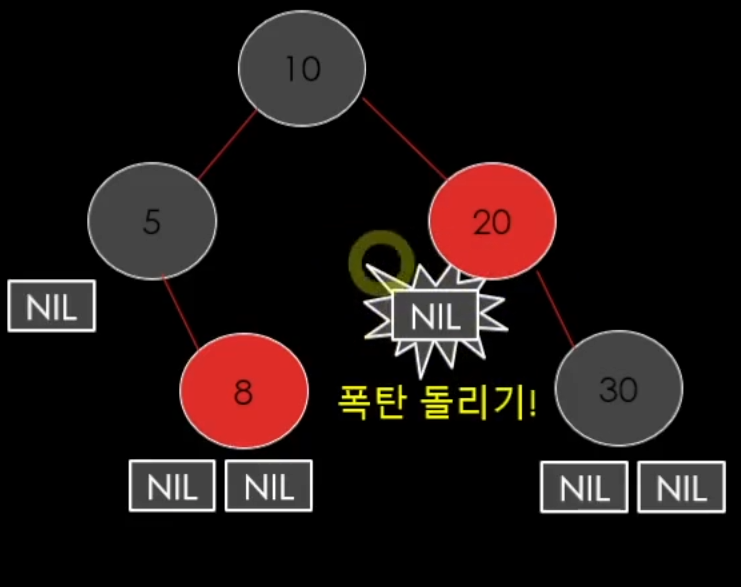
일단 블랙이 두개 있는 더블 블랙을 만들어준다. (폭탄)
이걸 안정화 시켜주는 것이 목표이다.

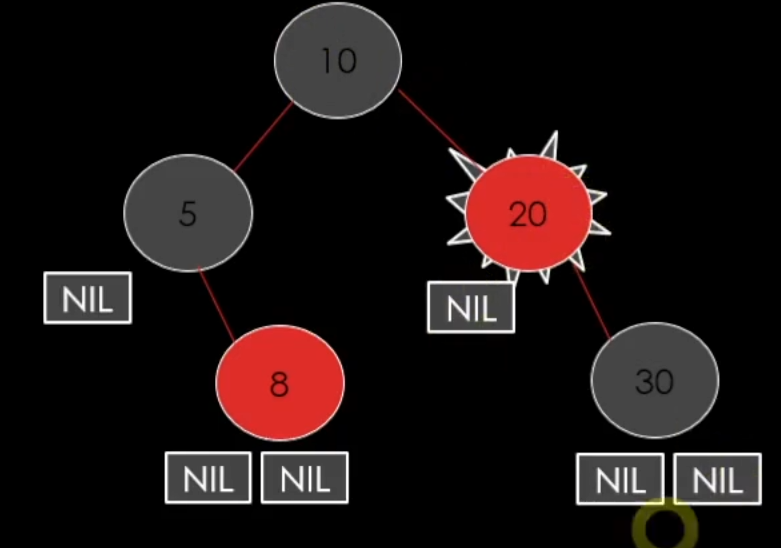
이걸 바로 올려버리면 왼쪽은 맞지만 오른쪽이 개수 하나가 올라가서 규칙을 위배하게 된다.

그래서 이것또한 공식이 있다.

case 2-1. Root가 더블 블랙일 때

이러한 경우에는 그냥 폭탄을 삭제 해주면 끝이 난다.
어차피 모든 경로가 루트를 통해서 가기 떄문에 모두에게 -1을 하는 것이여서 삭제하는 것이다.

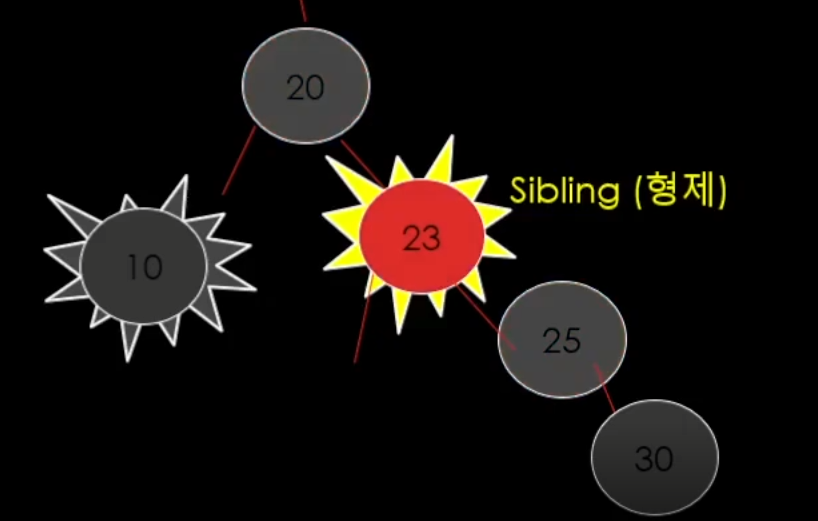
case 2-2. 더블 블랙의 형제가 Red이면 s = black, p = red (s와 p 색상 교환) (여기서 s는 형제) 그리고 더블 블랙 방향으로 rotate(p)를 시켜주면 해결 할 수 있다.

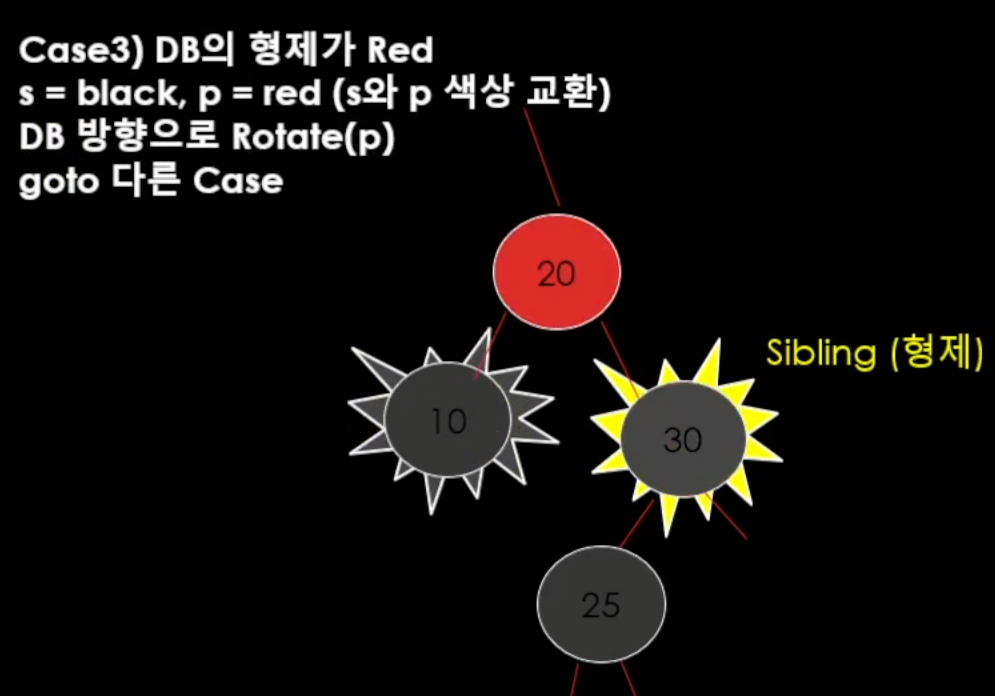
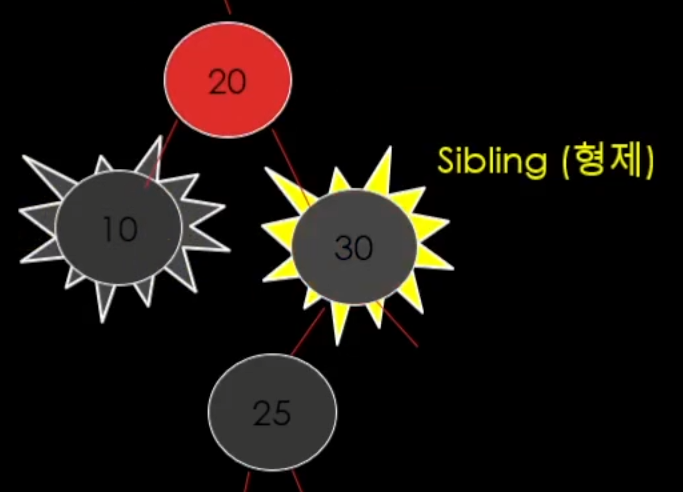
색상 바꾸고

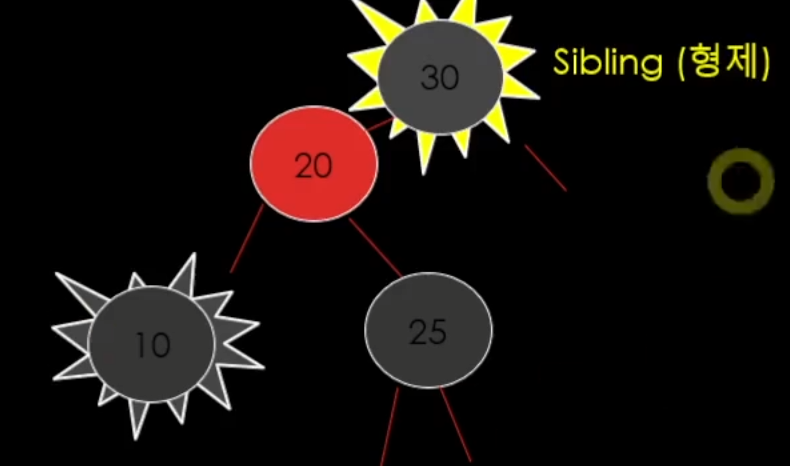
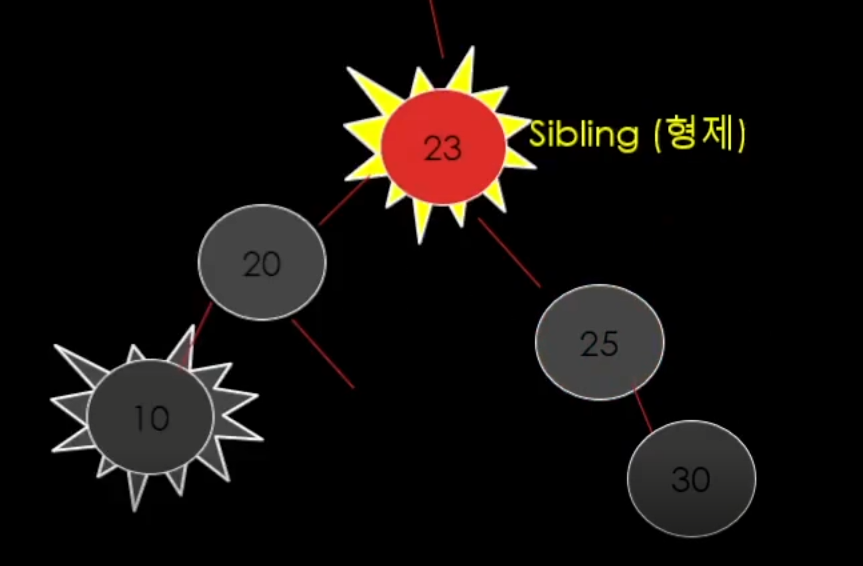
회전 하고

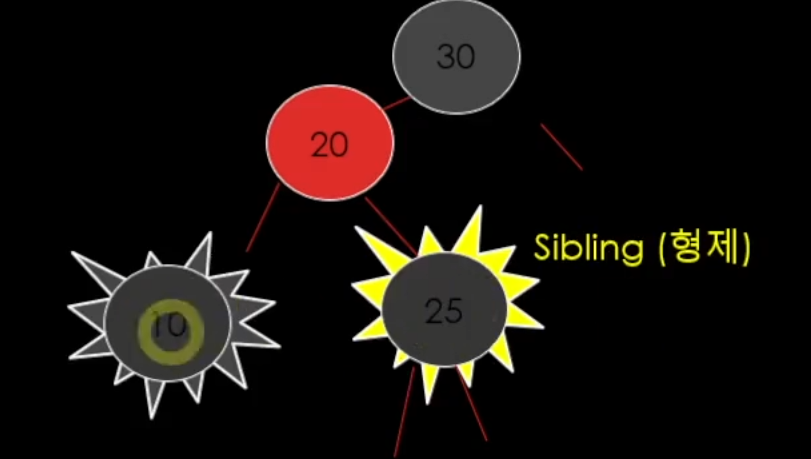
결국 이제 형제가 25가 되었기에 다른 case로 넘어가게 된다.

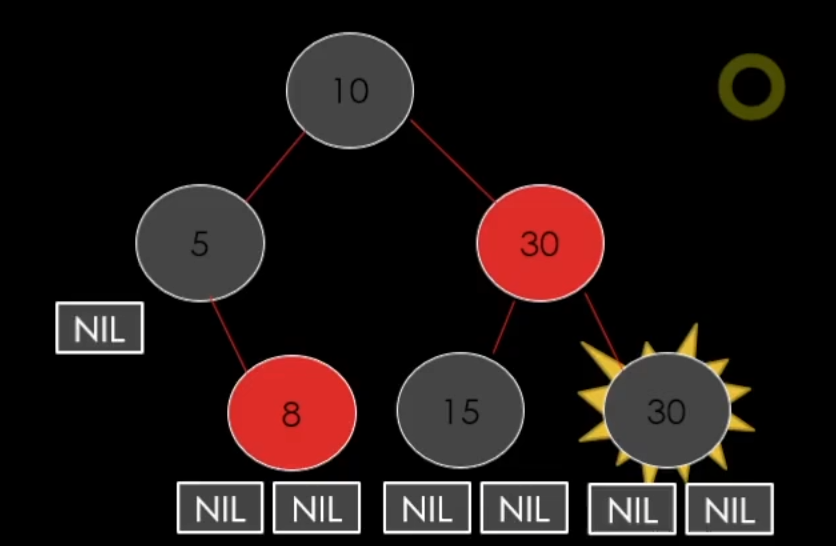
case 2-3. 더블 블랙의 형제가 Black && 형제의 양쪽 자식이 모두 Black일 때
추가 black(폭탄)을 parent에게 이전을 하고
p가 Red이면 Black이 되고, p가 Black이면 더블 블랙이 된다.
그리고 형제는 Red가 된다.

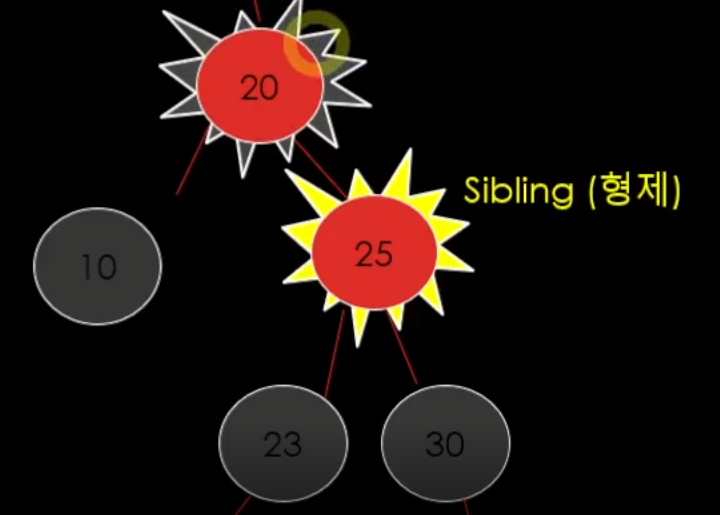
공식을 따라가면 이렇게 된다.

또 규칙이 더 있다..
case 2-4

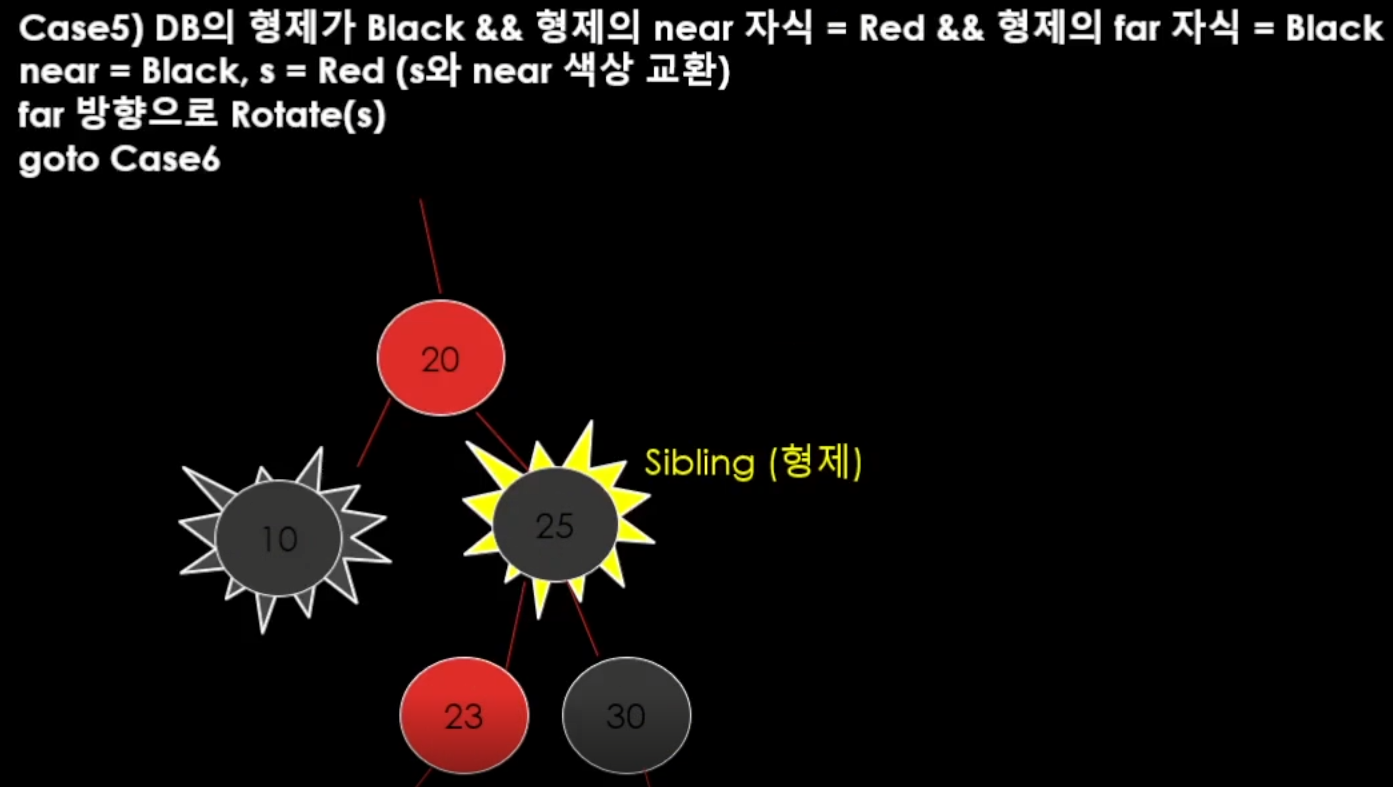
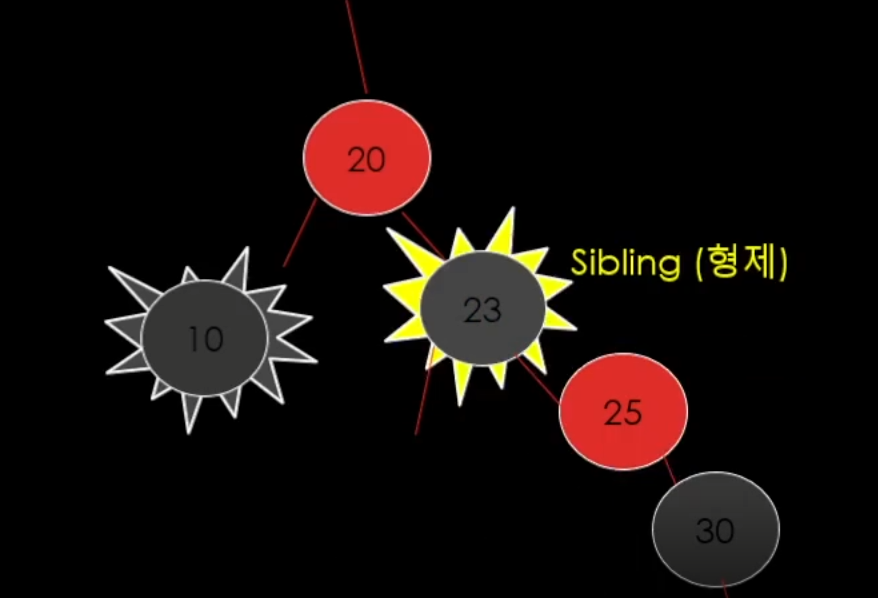
case 2-5

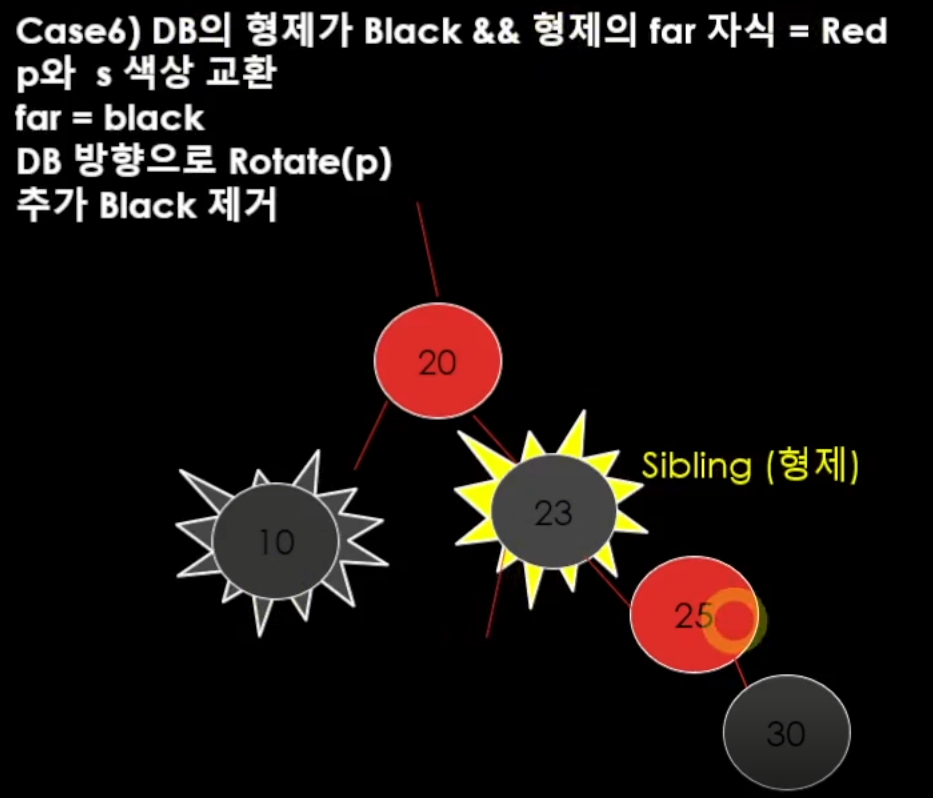
결론 & 마무리

그래서 결국 이러한 안정화를 하는 과정을 통해서 트리가 팽팽해지고 블랙의 개수가 일치가 된다!

솔직히 위에것들은 외우고, 구현하는 것은 솔직히 너무 시간도 많이 잡아먹고 사용하지도 않기 떄문에 하지 않을 것이다.

그래도 물어보면 대답은 할 줄 알아야 한다.

그래서 두줄 요약을 해보자면
추가는 삼촌 가챠이고
삭제는 폭탄 제거이다..

이 힘든 것을 구현을 한 것이 map이라고 볼 수 있다.

핵심적인 내용만 이해를 하자.

이진 탐색의 한계 추가/삭제 힘들다!
-> 이진 탐색 트리 추가/삭제 쉬워짐! but 한 쪽으로 쏠리면 연결리스트와 다를바 없음
-> 그래서 색상을 주고 여러가지 규칙들을 추가해 난리를 치는 Red Black Tree가 만들어짐!

이걸 이해했다??!!?!? map이나 쓰자