백준 12865: 평범한 배낭

델리만쥬 디퓨저·2025년 11월 30일

알고리즘

목록 보기

25/25

https://www.acmicpc.net/problem/12865

입출력 분석

물품의 수 100 * 버틸 수 있는 무게 100,000 = 10,000,000이므로 O(N^2)을 사용해도 시간 제한 2초 내로 가능
같은 이유로 메모리 제한 역시 넉넉하다

알고리즘 분석

과거의 선택과 현재의 무게를 고려해 물건을 선택하는 경우/선택하지 않는 경우를 통해 최적의 값을 구하려면 어떤 알고리즘이 필요할까?
DP

점화식

배낭 문제의 점화식은 다음과 같다.

v[i][j] = max(v[i-1][j], value + v[i-1][j-weight])

시나리오 분석

문제를 조금 더 쉽게 이해하기 위해, 점화식을 바탕으로 시나리오를 따라가면 다음과 같이 진행된다.

item1: 무게 6, 가치 13
item2: 무게 4, 가치 8
item3: 무게 3, 가치 6
item4: 무게 5, 가치 12

item1의 경우
1. 무게 1~5에 넣지 않는다
2. 무게 6~7에 가치 13을 입력한다

0   1   2   3   4   5   6   7  (배낭 무게)
    +---+---+---+---+---+---+---+
(1) | 0 | 0 | 0 | 0 | 0 | 13| 13|
    +---+---+---+---+---+---+---+

item2의 경우
1. 무게 1~3에 넣지 않는다
2. 무게 4~5에 가치 8을 입력한다
3. 무게 6에서 윗줄 값인 13과, item2의 가치인 8 + 남은 공간인 (6-4=2)의 윗줄 값을 비교해 더 큰 값인 13을 넣는다
4. 무게 7에서 윗줄 값인 13과, item2의 가치인 8 + 남은 공간인 (7-4=3)의 윗줄 값을 비교해 더 큰 값인 13을 넣는다

0   1   2   3   4   5   6   7  (배낭 무게)
    +---+---+---+---+---+---+---+
(1) | 0 | 0 | 0 | 0 | 0 | 13| 13|
(2) | 0 | 0 | 0 | 8 | 8 | 13| 13|
    +---+---+---+---+---+---+---+

item3의 경우
1. 무게 1~2에 넣지 않는다
2. 무게 3에 가치 6을 입력한다
3. 무게 4에서 윗줄 값인 8과, item3의 가치인 6 + 남은 공간인 (4-3=1)의 윗줄 값을 비교해 더 큰 값인 8을 넣는다
4. 무게 5에서 윗줄 값인 8과, item3의 가치인 6 + 남은 공간인 (5-3=2)의 윗줄 값을 비교해 더 큰 값인 8을 넣는다
5. 무게 6에서 윗줄 값인 13과, item3의 가치인 6 + 남은 공간인 (6-3=3)의 윗줄 값을 비교해 더 큰 값인 13을 넣는다
6. 무게 7에서 윗줄 값인 13과, item3의 가치인 6 + 남은 공간인 (7-3=4)의 윗줄 값을 비교해 더 큰 값인 14를 넣는다.

0   1   2   3   4   5   6   7  (배낭 무게)
    +---+---+---+---+---+---+---+
(1) | 0 | 0 | 0 | 0 | 0 | 13| 13|
(2) | 0 | 0 | 0 | 8 | 8 | 13| 13|
(3) | 0 | 0 | 6 | 8 | 8 | 13| 14|
    +---+---+---+---+---+---+---+

item4의 경우
1. 무게 1~4까지 넣지 않는다.
2. 무게 5에서 윗줄 값인 8과, item4의 가치인 12 + 남은 공간인 (5-5=0)의 윗줄 값을 비교해 더 큰 값인 12를 넣는다.
3. 무게 6에서 윗줄 값인 13과, item4의 가치인 12 + 남은 공간인 (6-5=1)의 윗줄 값을 비교해 더 큰 값인 13를 넣는다.
4. 무게 7에서 윗줄 값인 14과, item4의 가치인 12 + 남은 공간인 (7-5=2)의 윗줄 값을 비교해 더 큰 값인 14를 넣는다.

0   1   2   3   4   5   6   7  (배낭 무게)
    +---+---+---+---+---+---+---+
(1) | 0 | 0 | 0 | 0 | 0 | 13| 13|
(2) | 0 | 0 | 0 | 8 | 8 | 13| 13|
(3) | 0 | 0 | 6 | 8 | 8 | 13| 14|
(4) | 0 | 0 | 6 | 8 | 12| 13| 14|
    +---+---+---+---+---+---+---+

정답은 14가 되는 것을 확인할 수 있다.

풀이

import sys  
  
input = sys.stdin.readline  
  
n, k = map(int, input().split())  
  
item = [[0, 0]]  
dp = [[0] * (k + 1) for _ in range(n + 1)]  
  
for i in range(n):  
    new_item = list(map(int, input().split()))  
    item.append(new_item)  
  
for i in range(1, n + 1):  
    w, v = item[i]  
  
    if w > k:  
        for j in range(1, k+1):  
            dp[i][j] = dp[i-1][j]  
        continue  
  
    for j in range(1, w):  
        dp[i][j] = dp[i - 1][j]  
    for j in range(w, k + 1):  
        dp[i][j] = max(dp[i - 1][j], v + dp[i - 1][j - w])  
  
print(dp[n][k])

물건 무게가 배낭보다 큰 경우를 검사하지 않으면 인덱스 에러가 발생한다!

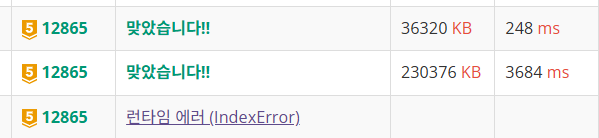
결과

정답은 맞았는데, 메모리와 시간이 엄청난 것을 확인할 수 있다.

더 효율적인 풀이

궁금해서 다른 사람들 풀이 구경하고 옴

import sys

input = sys.stdin.readline


def solve():
    n, k = map(int, input().split())

    items = [list(map(int, input().split())) for _ in range(n)]
    items.sort(key=lambda x: x[0], reverse=True)

    dp = {0: 0}

    for w, v in items:
        temp = {}

        for old_v, old_w in dp.items():
            new_v = old_v + v
            new_w = old_w + w

            if new_w > k:
                continue

            if new_w < dp.get(new_v, k + 1):
                temp[new_v] = new_w

        dp.update(temp)

    print(max(dp.keys()))


if __name__ == "__main__":
    solve()