문제
가로, 세로의 크기가 각각 100인 정사각형 모양의 흰색 도화지가 있다. 이 도화지 위에 가로, 세로의 크기가 각각 10인 정사각형 모양의 검은색 색종이를 색종이의 변과 도화지의 변이 평행하도록 붙인다. 이러한 방식으로 색종이를 한 장 또는 여러 장 붙인 후 색종이가 붙은 검은 영역의 넓이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 색종이의 수가 주어진다. 이어 둘째 줄부터 한 줄에 하나씩 색종이를 붙인 위치가 주어진다. 색종이를 붙인 위치는 두 개의 자연수로 주어지는데 첫 번째 자연수는 색종이의 왼쪽 변과 도화지의 왼쪽 변 사이의 거리이고, 두 번째 자연수는 색종이의 아래쪽 변과 도화지의 아래쪽 변 사이의 거리이다. 색종이의 수는 100 이하이며, 색종이가 도화지 밖으로 나가는 경우는 없다
출력
첫째 줄에 색종이가 붙은 검은 영역의 넓이를 출력한다.

논의
본 문제는 다음과 같이 수행된다.
- 붙일 색종이의 갯수를 입력받는다.
- 각 색종이들의 좌표를 입력받는다.
- 좌표를 바탕으로 겹치는 면적을 계산한다.
- 총 면적에서 겹치는 면적을 빼서 답을 구한다.
이 프로그램의 핵심은 색종이가 겹치는 부분을 어떻게 계산하느냐가 된다. 총 면적은 (사각형의 갯수 X 100 X 100)이므로 겹치는 부분만 계산한다면 최종 답을 도출해낼 수 있다.
사각형이 두개인 경우
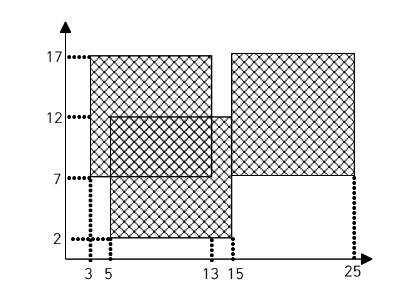
사각형의 좌표를 바탕으로 면적 범위를 계산해 보자. 좌표가 (3, 7)인 사각형을 입력받는다. 그렇게 되면 해당 사각형의 면적은 (3, 7)에서 (13, 17)가 된다. 또 다른 사각형을 입력받아 보자. (5, 2)인 사각형을 입력받으면 좌표의 범위는 (5, 2)에서 (15, 12)가 된다.
그럼 이 둘의 겹치는 범위를 계산해 보자. 왼쪽 하단은 둘 중 큰 값을, 오른쪽 상단은 둘 중 작은 값을 구하면 간단하게 겹치는 부분을 구할 수 있다. 두 사각형이 겹치는 부분은 (5, 7)에서 (13, 12)가 된다. (13-5) X (12-7) = 40이 된다.
그러므로 두 사각형의 크기인 200에서 겹치는 부분인 40을 빼면 두 사각형의 총 면적은 160이 된다.
사각형이 여러개인 경우
이중 반복문을 사용하여 겹치는 면적을 모두 계산한다. 각각의 사각형을 다른 사각형들과 비교해 겹치는 면적을 계산한 뒤 변수에 저장한다. 이때 겹치는 면적을 한번만 계산하도록 주의해야 할 것이다.
1차 시도
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
public static void main(String args[]) {
Scanner s = new Scanner(System.in);
int SquareNum = s.nextInt();
int Total = 0;
List<int[]> list = new ArrayList<>();
for (int i = 0; i < SquareNum; i++) { // 좌표를 리스트에 저장
int x = s.nextInt();
int y = s.nextInt();
list.add(new int[] { x, y });
}
for (int i = 0; i < SquareNum - 1; i++) {
int[] arr = list.get(i); // 좌표를 꺼내온다
for (int j = i + 1; j < SquareNum; j++) {
int[] arr2 = list.get(j); // 비교할 좌표를 꺼내온다
int minx = 0, miny = 0, maxx = 0, maxy = 0;
if (arr[0] + 10 <= arr2[0] || arr2[0] + 10 <= arr[0]
|| (arr[1] + 10 <= arr2[1] || arr2[1] + 10 <= arr[1])) { // 범위가 겹치는지 검사한다
continue;
}
if (arr[0] > arr2[0]) { // 겹치는 범위를 계산한다.
minx = arr[0];
maxx = arr2[0] + 10;
} else {
minx = arr2[0];
maxx = arr[0] + 10;
}
if (arr[1] > arr2[1]) {
miny = arr[1];
maxy = arr2[1] + 10;
} else {
miny = arr2[1];
maxy = arr[1] + 10;
}
Total += Math.abs((maxx - minx) * (maxy - miny)); // 혹시 음수가 발생할 수 있으니 절대값으로 변환해 저장한다
}
}
System.out.println(SquareNum * 100 - Total);
}
}
리스트를 생성해 좌표 x, y를 저장한 뒤 각각을 비교하는 방식으로 구현하였다. 이때 색종이끼리 범위가 겹치는지 확인한다. 겹치면 위에서 말한 일련의 방식으로 범위를 계산한다.
하지만 이러한 방식은 예상값보다 더 적은 숫자가 나오며 실패하게 된다.
왜 실패했을까?
(0, 0), (5, 5), (8, 8)을 대입해보면 알 수 있다. 실제로 계산해 보면 226이 나오지만 코드상으로는 222가 나온다. 사각형이 여러번 겹치는 부분에 대한 문제가 있기 때문이다. 해당 코드는 한 번 겹치는 부분에 대해서는 정상적으로 수행되지만 여러번 겹치는 부분에 대해서는 처리가 되지 않는다. 또한 실패와는 별개로 음수로 저장될 리가 없으므로 절대값으로 변환할 필요도 없다.
따라서 다른 방식으로 접근하기로 했다. 100*100 크기의 배열을 선언한다. 이후 입력된 사각형의 좌표에 따라 그 범위에 해당하는 칸에 1을 더한다. 이렇게 계산할 경우 0이 아닌 부분의 칸의 개수만 구하면 전체 면적을 구할 수 있을 것이다.
- 100*100 배열을 선언한다.
- 입력받은 좌표를 통해 범위에 해당하는 칸에 모두 1을 더한다.
- 0이 아닌 칸의 갯수를 센다.
최종 코드
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
public static void main(String args[]) {
Scanner s = new Scanner(System.in);
int SquareNum = s.nextInt();
int[][] arr = new int[100][100]; // 100*100 배열 선언
for (int i = 0; i < SquareNum; i++) {
int x = s.nextInt();
int y = s.nextInt();
for (int j = x; j < x + 10; j++) { // 입력된 범위의 칸에 1을 더해준다
for (int k = y; k < y + 10; k++) {
arr[j][k] += 1;
}
}
}
int count = 0;
for (int i = 0; i < 100; i++) { // 0 이상인 경우 색칠된 범위이므로 더해준다
for (int j = 0; j < 100; j++) {
if (arr[i][j] > 0)
count += 1;
}
}
System.out.println(count);
}
}다음과 같은 코드가 완성된다. 이전의 코드보다 훨씬 깔끔한 것을 확인할 수 있다.
