하노이 타워

하노이 타워는 다음과 같은 규칙을 갖는다.

1. 한 번에 하나의 원반만을 옮길 수 있다.
2. 큰 원반 위에 작은 원반을 놓을 수 없다.
3. 기둥 사이에서 원반을 직접 옮길 수 없으며, 중간에 보조 기둥을 사용하여야 한다.

이 문제를 해결하기 위해서는 다음과 같은 아이디어를 사용한다.

1. 기본적으로 원반이 하나일 때는 시작 기둥에서 목표 기둥으로 바로 옮긴다.
2. 그 외의 경우, 재귀적으로 다음을 수행한다.
   2-1. 가장 큰 원반을 제외한 나머지 원반들을 시작 기둥에서 보조 기둥으로 옮긴다.
   2-2. 가장 큰 원반을 시작 기둥에서 목표 기둥으로 옮긴다.
   2-3. 나머지 원반들을 보조 기둥에서 목표 기둥으로 옮긴다.

이 과정을 반복해 원반들을 목표 기둥으로 옮긴다. 재귀 호출을 통해 하위 문제를 해결하면서 전체 문제를 해결하는 방식으로 동작한다.

자바 구현 코드는 다음과 같다.

public class HanoiTower {
    public static void hanoi(int n, char 시작기둥, char 보조기둥, char 목표기둥) {
        if (n == 1) {
            System.out.println(시작기둥 + "에서 " + 목표기둥 + "로 원반 1을 옮깁니다.");
            return;
        }

        hanoi(n - 1, 시작기둥, 목표기둥, 보조기둥);
        System.out.println(시작기둥 + "에서 " + 목표기둥 + "로 원반 " + n + "을 옮깁니다.");
        hanoi(n - 1, 보조기둥, 시작기둥, 목표기둥);
    }

    public static void main(String[] args) {
        int 원반_개수 = 3;
        hanoi(원반_개수, 'A', 'B', 'C');
    }
}

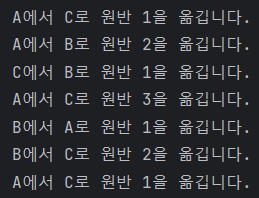
코드를 실행하면 다음과 같은 결과가 출력된다.

하노이 타워의 시간 복잡도

하노이 타워는 재귀적인 방식으로 해결되며, 각 재귀 호출마다 2개의 하위 호출이 이루어지므로 2^n번의 호출이 발생한다. 따라서 원반 수가 증가할수록 지수적으로 시작이 증가하며 시간 복잡도가 O(2^n)으로 증가한다.